题目

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回 网格坐标 result 的 2D列表 ，其中 result[i] = [ri, ci] 表示雨水可以从单元格 (ri, ci) 流向 太平洋和大西洋 。

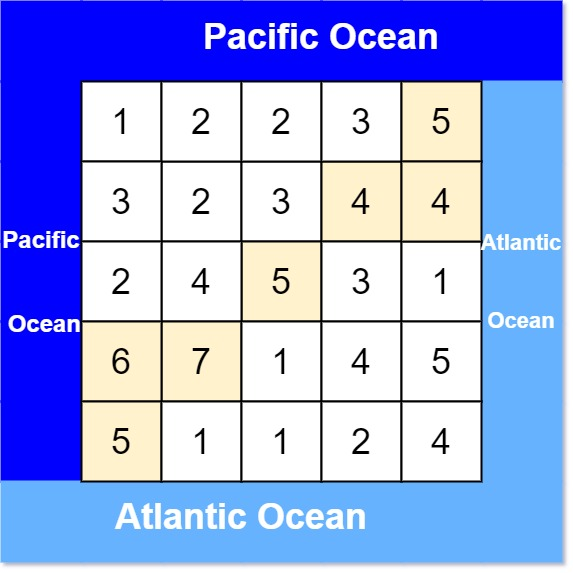
示例 1： image.png

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

提示：

m == heights.length
n == heights[r].length
1 <= m, n <= 200
0 <= heights[r][c] <= 10^5

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/pacific-atlantic-water-flow
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

题目很好理解，要求和太平洋、大西洋都连通的坐标点。

如果按常规思路对每一个点417. 太平洋大西洋水流问题 - 图2进行417. 太平洋大西洋水流问题 - 图3遍历，在时间上，有417. 太平洋大西洋水流问题 - 图4个点，每个点要遍历417. 太平洋大西洋水流问题 - 图5时间，时间复杂度为417. 太平洋大西洋水流问题 - 图6#card=math&code=O%28m%5E2%2An%5E2%29&id=ICkhF)，会超时。在空间上，除了遍历时常用到的417. 太平洋大西洋水流问题 - 图7数组外，还需要空间记录417. 太平洋大西洋水流问题 - 图8点搜索的结果，即是否同时与太平洋、大西洋都连通。所以需要转变思路。

如果逆向考虑，从边界开始搜索，即分别从太平洋、大西洋进行搜索，分别记录两个水域可以到达的位置，最后返回两个集合的交集即可。重点是，从四个边界分别搜索一遍矩阵，时间复杂度是417. 太平洋大西洋水流问题 - 图9#card=math&code=O%28m%2An%29&id=D6BSj)。

代码

  1. class Solution {
  2.     int[][] dirs = {{0, -1}, {0, 1}, {1, 0}, {-1, 0}};
  4.     public List<List<Integer>> pacificAtlantic(int[][] heights) {
  5.         int m = heights.length;
  6.         int n = heights[0].length;
  7.         // pacific[i][j] 表示[i,j]这一坐标能否流到太平洋
  8.         boolean[][] pacific = new boolean[m][n];
  9.         // atlantic[i][j] 表示[i,j]这一坐标能否流到大西洋
  10.         boolean[][] atlantic = new boolean[m][n];
  11.         for (int i = 0; i < m; i++) {
  12.             // 从第一列边界开始搜索，能搜到的位置就表示和太平洋连通，pacific数组可以和下面循环内第一个dfs共用
  13.             dfs(i, 0, m, n, heights, pacific);
  14.             // 从第n-1列边界开始搜索，能搜到的位置就表示和大西洋连通，atlantic数组可以和下面循环内第二个dfs共用
  15.             dfs(i, n - 1, m, n, heights, atlantic);
  16.         }
  17.         for (int i = 0; i < n; i++) {
  18.             // 从第一行边界开始搜索，能搜到的位置就表示和太平洋连通
  19.             dfs(0, i, m, n, heights, pacific);
  20.             // 从第m-1行边界开始搜索，能搜到的位置就表示和大西洋连通
  21.             dfs(m - 1, i, m, n, heights, atlantic);
  22.         }
  23.         List<List<Integer>> ans = new ArrayList<>();
  24.         for (int i = 0; i < m; i++) {
  25.             for (int j = 0; j < n; j++) {
  26.                 // 将和太平洋、大西洋都连通的点添加到结果集
  27.                 if (pacific[i][j] && atlantic[i][j]) {
  28.                     ans.add(List.of(i, j));
  29.                 }
  30.             }
  31.         }
  32.         return ans;
  33.     }
  35.     private void dfs(int row, int col, int m, int n, int[][] heights, boolean[][] reachable) {
  36.         reachable[row][col] = true;
  37.         for (int[] dir : dirs) {
  38.             int nr = dir[0] + row;
  39.             int nc = dir[1] + col;
  40.             if (nr < 0 || nr >= m || nc < 0 || nc >= n || reachable[nr][nc] || heights[nr][nc] < heights[row][col]) {
  41.                 continue;
  42.             }
  43.             dfs(nr, nc, m, n, heights, reachable);
  44.         }
  45.     }
  46. }