77. 组合

题目

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/combinations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

经典的回溯问题，不同于排列问题，组合不考虑顺序，例如和是同一种组合方式，因此需要避免这两者重复地加入结果集。

第一种思路是，和我们把它当做数学题的思路一样，比如，到中选两个，那么第一个数有四种选择，可选，第二个数的选择就和第一个数有关系，只能选大于第一个数的，因为前面提到的，组合不讲究顺序，需要避免重复添加。这种方法的递归树如下：

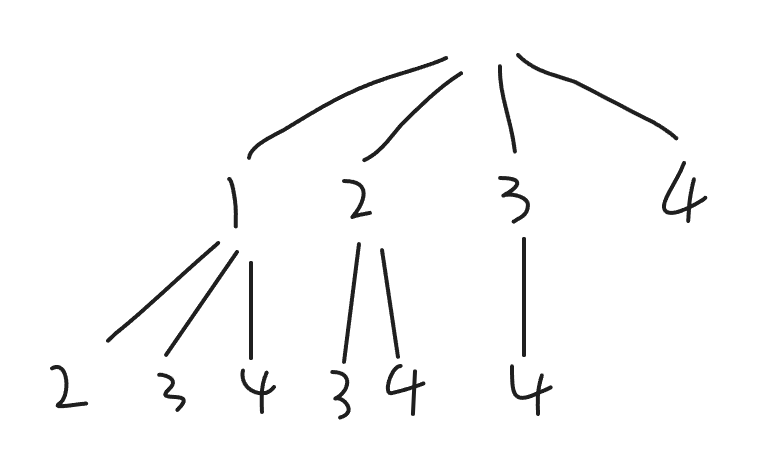
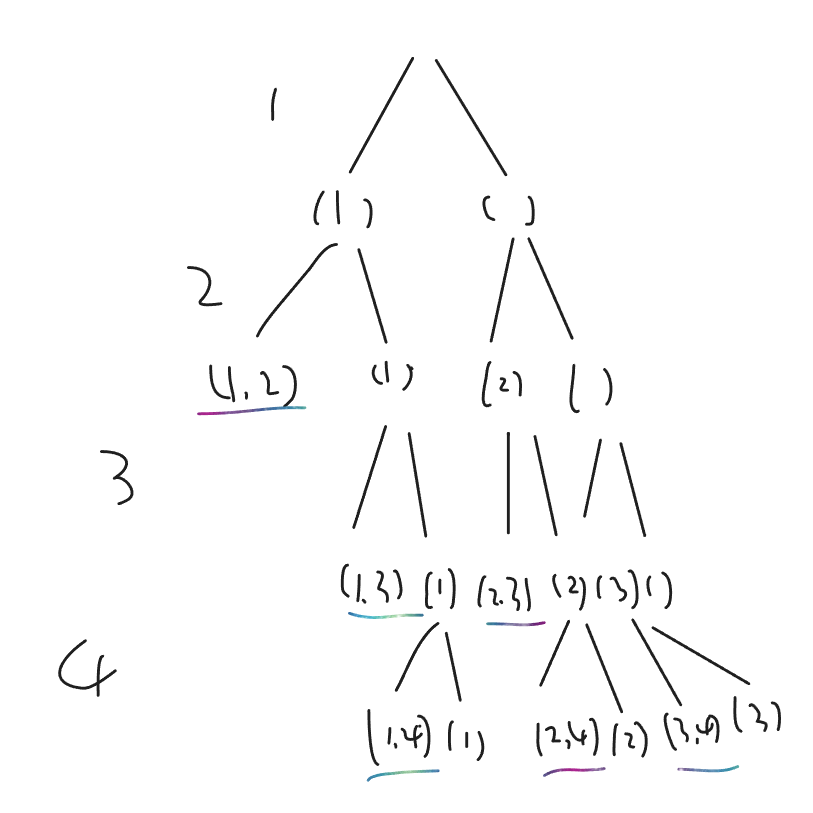
第二种思路是可以依次考虑每个数选与不选，选够了个就表示获得了一种组合方式。这种方法的递归树如下图，从开始考虑，每一个分支表示当前数选与不选，左分支为选，右分支不选，划横线的就是最终的种组合方式，可以看出不同于第一种方法答案都在一层，这里不在一层。鼠标画画实在太难了，丑的自己也看不下去…

代码

方法一 考虑当前一步选哪个数

class Solution {
    List<List<Integer>> ans;
    public List<List<Integer>> combine(int n, int k) {
        ans = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();
        dfs(1, k, n, path);
        return ans;
    }
    private void dfs(int begin, int k, int n, Deque<Integer> path) {
        if (path.size() == k) {
            ans.add(new ArrayList<>(path));
            return;
        }
        // 当前位置考虑的起始范围由上一个数决定，只能往后考虑
        for (int i = begin; i <= n; i++) {
            path.push(i);
            dfs(i + 1, k, n, path);
            path.poll();
        }
    }
}

方法二 从1到n考虑每个数选与不选

class Solution {
    List<List<Integer>> ans;
    public List<List<Integer>> combine(int n, int k) {
        ans = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();
        dfs(1, k, n, path);
        return ans;
    }
    private void dfs(int index, int k, int n, Deque<Integer> path) {
        if (path.size() == k) {
            ans.add(new ArrayList<>(path));
            return;
        }
        if (index > n) {
            return;
        }
        // 选择当前数index
        path.push(index);
        dfs(index + 1, k, n, path);
        path.poll();
        // 不选当前数index
        dfs(index + 1, k, n, path);
    }
}