题目

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

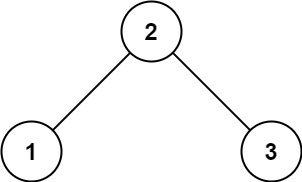
示例 1: image.png

输入: root = [2,1,3]
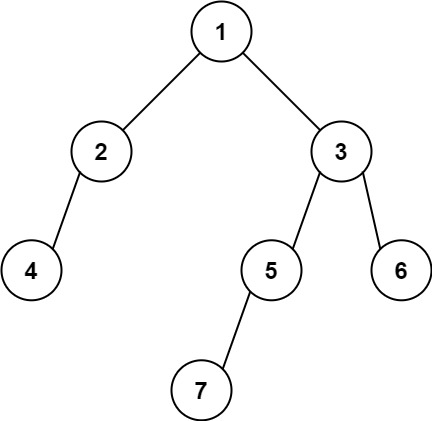
输出: 1

示例 2: image.png

输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示:

二叉树的节点个数的范围是 [1,10^4]
-2^31 <= Node.val <= 2^31 - 1

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/find-bottom-left-tree-value
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

层序遍历，最后一层的第一个元素就是答案。写法一是最直接的，写法二稍微有点巧妙。

代码

BFS写法一

  1. /**
  2.  * Definition for a binary tree node.
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode() {}
  8.  *     TreeNode(int val) { this.val = val; }
  9.  *     TreeNode(int val, TreeNode left, TreeNode right) {
  10.  *         this.val = val;
  11.  *         this.left = left;
  12.  *         this.right = right;
  13.  *     }
  14.  * }
  15.  */
  16. class Solution {
  17.     public int findBottomLeftValue(TreeNode root) {
  18.         Queue<TreeNode> q = new ArrayDeque<>();
  19.         q.offer(root);
  20.         int ans = 0;
  21.         while (!q.isEmpty()) {
  22.             int size = q.size();
  23.             for (int i = 0; i < size; i++) {
  24.                 TreeNode cur = q.poll();
  25.                 if (i == 0) {
  26.                     ans = cur.val;
  27.                 }
  28.                 if (cur.left != null) {
  29.                     q.offer(cur.left);
  30.                 }
  31.                 if (cur.right != null) {
  32.                     q.offer(cur.right);
  33.                 }
  34.             }
  35.         }
  36.         return ans;
  37.     }
  38. }

BFS写法二

一个更巧妙的方法是先入队右孩子，这样可以保证左下角的节点最后一个出队。

  1. class Solution {
  2.     public int findBottomLeftValue(TreeNode root) {
  3.         Queue<TreeNode> q = new ArrayDeque<>();
  4.         q.offer(root);
  5.         int ans = 0;
  6.         while (!q.isEmpty()) {
  7.             TreeNode cur = q.poll();
  8.             ans = cur.val;
  9.             if (cur.right != null) {
  10.                 q.offer(cur.right);
  11.             }
  12.             if (cur.left != null) {
  13.                 q.offer(cur.left);
  14.             }
  15.         }
  16.         return ans;
  17.     }
  18. }

DFS

也可以进行深度优先搜索，递归时携带一个变量，表示当前高度，如果大于最大的高度就更新当前值为ans。

先访问左孩子可以保证更新ans时一定使用左孩子的值更新ans。

  1. class Solution {
  2.     int maxh = -1;
  3.     int val = 0;
  5.     public int findBottomLeftValue(TreeNode root) {
  6.         dfs(root, 0);
  7.         return val;
  8.     }
  10.     private void dfs(TreeNode root, int h) {
  11.         if (root == null) {
  12.             return;
  13.         }
  14.         if (h > maxh) {
  15.             maxh = h;
  16.             val = root.val;
  17.         }
  18.         dfs(root.left, h + 1);
  19.         dfs(root.right, h + 1);
  20.     }
  21. }