2245. 转角路径的乘积中最多能有几个尾随零

题目

给你一个二维整数数组 grid ，大小为 m x n，其中每个单元格都含一个正整数。

转角路径 定义为：包含至多一个弯的一组相邻单元。具体而言，路径应该完全 向水平方向 或者 向竖直方向 移动过弯（如果存在弯），而不能访问之前访问过的单元格。在过弯之后，路径应当完全朝 另一个 方向行进：如果之前是向水平方向，那么就应该变为向竖直方向；反之亦然。当然，同样不能访问之前已经访问过的单元格。

一条路径的 乘积 定义为：路径上所有值的乘积。

请你从 grid 中找出一条乘积中尾随零数目最多的转角路径，并返回该路径中尾随零的数目。

注意：

水平 移动是指向左或右移动。
竖直 移动是指向上或下移动。

示例 1：

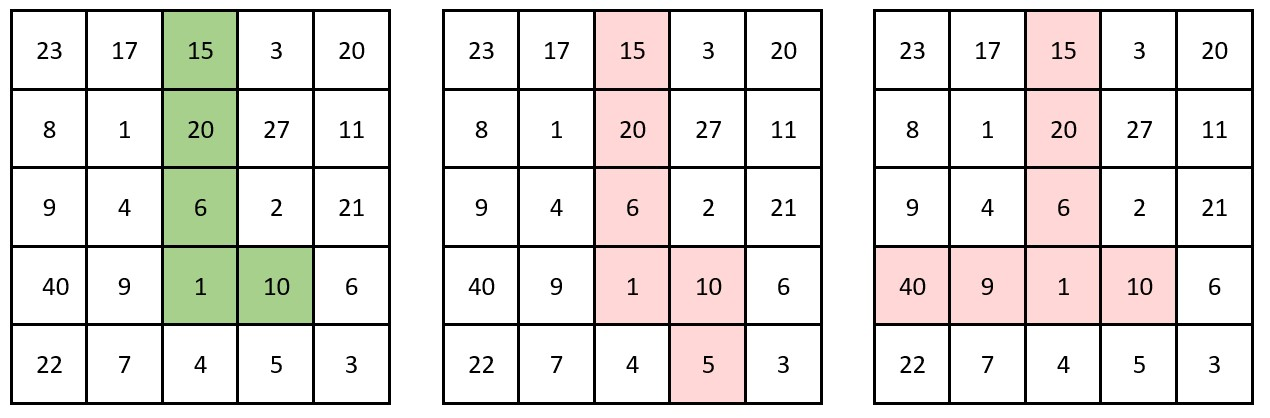
输入：grid = [[23,17,15,3,20],[8,1,20,27,11],[9,4,6,2,21],[40,9,1,10,6],[22,7,4,5,3]]
输出：3
解释：左侧的图展示了一条有效的转角路径。
其乘积为 15 20 6 1 10 = 18000 ，共计 3 个尾随零。
可以证明在这条转角路径的乘积中尾随零数目最多。

中间的图不是一条有效的转角路径，因为它有不止一个弯。
右侧的图也不是一条有效的转角路径，因为它需要重复访问已经访问过的单元格。

示例 2：

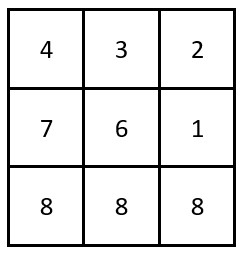
输入：grid = [[4,3,2],[7,6,1],[8,8,8]]
输出：0
解释：网格如上图所示。
不存在乘积含尾随零的转角路径。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 10^5
1 <= m * n <= 10^5
1 <= grid[i][j] <= 1000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-trailing-zeros-in-a-cornered-path
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

第一反应是dfs，也因为做过172题知道尾0就是找每个数2和5的因子个数，个数较小的数目就是0的个数。不过就是只能转一次弯不好处理，最后觉得代码没问题了还是过不去…

比赛结束后知道原来正确的做法不是dfs，正确的做法是枚举拐点，选择两个方向，有四种可能，分别求尾0的个数，因为要求矩阵某一水平或竖直线段内2或者5的因子个数，所以可以先使用前缀和数组记录每行和每列2和5的因子数目，之后可以O(1)时间求得某一水平或竖直线段内2或者5的因子个数。

虽然思想不难，但不得不说，代码是真的不好写…一个下标错了就错了

代码

class Solution {
    public int maxTrailingZeros(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        // 每行的前缀和数组，f2[i,:]表示grid第i-1行2因子个数的前缀和数组，其中i属于[1,m]，f5同理
        int[][] f2 = new int[m + 1][n + 1];
        // 每列的前缀和数组，g2[:,j]表示grid第j-1列2因子个数的前缀和数组，其中j属于[1,n]，g5同理
        int[][] g2 = new int[m + 1][n + 1];
        int[][] f5 = new int[m + 1][n + 1];
        int[][] g5 = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                int num = grid[i - 1][j - 1];
                // num 2的因子个数
                int two = 0;
                // num 5的因子个数
                int five = 0;
                while (num % 2 == 0) {
                    num /= 2;
                    two++;
                }
                while (num % 5 == 0) {
                    num /= 5;
                    five++;
                }
                f2[i][j] = f2[i][j - 1] + two;
                f5[i][j] = f5[i][j - 1] + five;
                g2[i][j] = g2[i - 1][j] + two;
                g5[i][j] = g5[i - 1][j] + five;
            }
        }
        int ans = 0;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // 上左，内层Math.min表示尾0个数取决于2和5因子数目更少的那一个，然后外层Math.max更新ans
                ans = Math.max(ans, Math.min(g2[i][j] + f2[i][j - 1], g5[i][j] + f5[i][j - 1]));
                // 上右
                ans = Math.max(ans, Math.min(g2[i][j] + f2[i][n] - f2[i][j], g5[i][j] + f5[i][n] - f5[i][j]));
                // 左下
                ans = Math.max(ans, Math.min(f2[i][j] + g2[m][j] - g2[i][j], f5[i][j] + g5[m][j] - g5[i][j]));
                // 右下
                ans = Math.max(ans, Math.min(f2[i][n] - f2[i][j - 1] + g2[m][j] - g2[i][j], f5[i][n] - f5[i][j - 1] + g5[m][j] - g5[i][j]));
            }
        }
        return ans;
    }
}