1823. 找出游戏的获胜者 - 《算法》

题目
思路
代码

题目

共有 n 名小伙伴一起做游戏。小伙伴们围成一圈，按顺时针顺序从 1 到 n 编号。确切地说，从第 i 名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置，其中 1 <= i < n ，从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。

游戏遵循如下规则：

从第 1 名小伙伴所在位置开始。
沿着顺时针方向数 k 名小伙伴，计数时需要包含起始时的那位小伙伴。逐个绕圈进行计数，一些小伙伴可能会被数过不止一次。
你数到的最后一名小伙伴需要离开圈子，并视作输掉游戏。
如果圈子中仍然有不止一名小伙伴，从刚刚输掉的小伙伴的顺时针下一位小伙伴开始，回到步骤 2 继续执行。
否则，圈子中最后一名小伙伴赢得游戏。
给你参与游戏的小伙伴总数 n ，和一个整数 k ，返回游戏的获胜者。

示例 1：

输入：n = 5, k = 2
输出：3
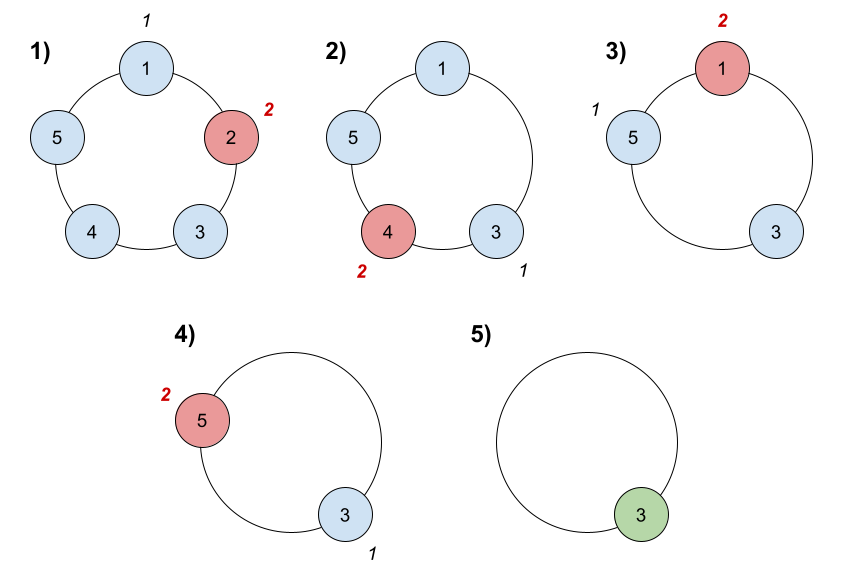
解释：游戏运行步骤如下：

从小伙伴 1 开始。
顺时针数 2 名小伙伴，也就是小伙伴 1 和 2 。
小伙伴 2 离开圈子。下一次从小伙伴 3 开始。
顺时针数 2 名小伙伴，也就是小伙伴 3 和 4 。
小伙伴 4 离开圈子。下一次从小伙伴 5 开始。
顺时针数 2 名小伙伴，也就是小伙伴 5 和 1 。
小伙伴 1 离开圈子。下一次从小伙伴 3 开始。
顺时针数 2 名小伙伴，也就是小伙伴 3 和 5 。
小伙伴 5 离开圈子。只剩下小伙伴 3 。所以小伙伴 3 是游戏的获胜者。

示例 2：

输入：n = 6, k = 5
输出：1
解释：小伙伴离开圈子的顺序：5、4、6、2、3 。小伙伴 1 是游戏的获胜者。

提示：

1 <= k <= n <= 500

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-the-winner-of-the-circular-game
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

经典的约瑟夫环问题，下面用三种方式解，可以自己模拟、也可以使用类库中的队列、也可以使用数学法。

代码

数组模拟

class Solution {
    public int findTheWinner(int n, int k) {
        // true表示淘汰
        boolean[] arr = new boolean[n];
        // 还剩 cnt 个人未淘汰
        int cnt = n;
        // 遍历下标
        int i = 0;
        while (cnt > 1) {
            // 要淘汰的选手
            int g = 0;
            int j = 0;
            // 一轮报数 k 次
            while (j < k) {
                // 未淘汰的才参与报数
                if (!arr[i]) {
                    j++;
                    // 更新要淘汰的人
                    g = i;
                }
                i = (i + 1) % n;
            }
            arr[g] = true;
            cnt--;
        }
        for (int j = 0; j < n; ++j) {
            if (!arr[j]) return j + 1;
        }
        return -1;
    }
}

队列模拟

class Solution {
    public int findTheWinner(int n, int k) {
        Queue<Integer> q = new LinkedList<>();
        // 1到n依次入队
        for (int i = 1; i <= n; i++) {
            q.offer(i);
        }
        // 出队n-1个人
        for (int i = 1; i < n; i++) {
            // 前k-1个人可以在这一轮幸免，将他们移到队尾
            for (int j = 0; j < k - 1; j++) {
                q.offer(q.poll());
            }
            // 将第k个人移出去
            q.poll();
        }
        // 最后留下的人
        return q.poll();
    }
}

数学法

公式的递推过程见「这里」

class Solution {
    public int findTheWinner(int n, int k) {
        int p = 0;
        for (int i = 2; i <= n; i++) {
            p = (p + k) % i;
        }
        return p + 1;
    }
}