2267. 检查是否有合法括号字符串路径

题目

一个括号字符串是一个 非空 且只包含 ‘(‘ 和 ‘)’ 的字符串。如果下面 任意 条件为 真 ，那么这个括号字符串就是 合法的 。

字符串是 () 。
字符串可以表示为 AB（A 连接 B），A 和 B 都是合法括号序列。
字符串可以表示为 (A) ，其中 A 是合法括号序列。
给你一个 m x n 的括号网格图矩阵 grid 。网格图中一个 合法括号路径 是满足以下所有条件的一条路径：

路径开始于左上角格子 (0, 0) 。
路径结束于右下角格子 (m - 1, n - 1) 。
路径每次只会向 下 或者向 右 移动。
路径经过的格子组成的括号字符串是 合法 的。
如果网格图中存在一条 合法括号路径 ，请返回 true ，否则返回 false 。

示例 1：

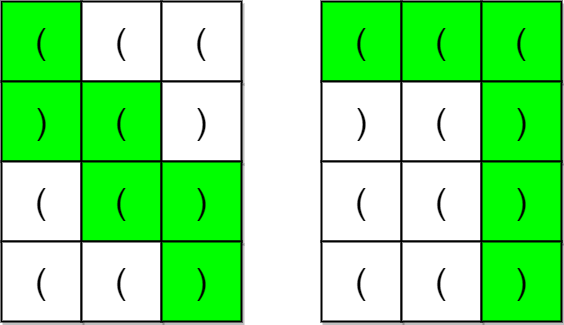
输入：grid = [[“(“,”(“,”(“],[“)”,”(“,”)”],[“(“,”(“,”)”],[“(“,”(“,”)”]]
输出：true
解释：上图展示了两条路径，它们都是合法括号字符串路径。
第一条路径得到的合法字符串是 “()(())” 。
第二条路径得到的合法字符串是 “((()))” 。
注意可能有其他的合法括号字符串路径。

示例 2：

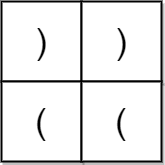
输入：grid = [[“)”,”)”],[“(“,”(“]]
输出：false
解释：两条可行路径分别得到 “))(“ 和 “)((“ 。由于它们都不是合法括号字符串，我们返回 false 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 100
grid[i][j] 要么是 ‘(‘ ，要么是 ‘)’ 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/check-if-there-is-a-valid-parentheses-string-path
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这道题告诉我思路如果是错的，花再多时间都是做不出来的…

「这个」题解很是优秀，几句话就点名了本题的要点，而且给出了最优空间的解法。

按其思路，写了一个三维的，见代码一。

代码

代码一 三维DP

class Solution {
    public boolean hasValidPath(char[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        // 将(看作是1，)看做是-1后，合法的状态取值最小为0，最大为(m + n - 1) / 2，因此合法的状态最多有(m + n - 1) / 2 + 1种
        int k = (m + n - 1) / 2 + 1;
        // 前两维多加了一个长度，方便初始化
        boolean[][][] dp = new boolean[m + 1][n + 1][k];
        // 初始化，保证了grid[0][0]为左括号时，可以正确地状态转移
        dp[1][0][0] = true;
        dp[0][1][0] = true;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                int c = grid[i - 1][j - 1] == '(' ? 1 : -1;
                // l表示合法的状态，介于[0,k)，同时，l要>=0且l-c要小于k，所以l的范围就是下面的形式
                for (int l = Math.max(c, 0); l < Math.min(k, k + c); l++) {
                    dp[i][j][l] = dp[i - 1][j][l - c] || dp[i][j - 1][l - c];
                }
            }
        }
        return dp[m][n][0];
    }
}