386. 字典序排数

题目

给你一个整数 n ，按字典序返回范围 [1, n] 内所有整数。

你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。

示例 1：

输入：n = 13
输出：[1,10,11,12,13,2,3,4,5,6,7,8,9]

示例 2：

输入：n = 2
输出：[1,2]

提示：

1 <= n <= 5 * 10^4

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/lexicographical-numbers
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

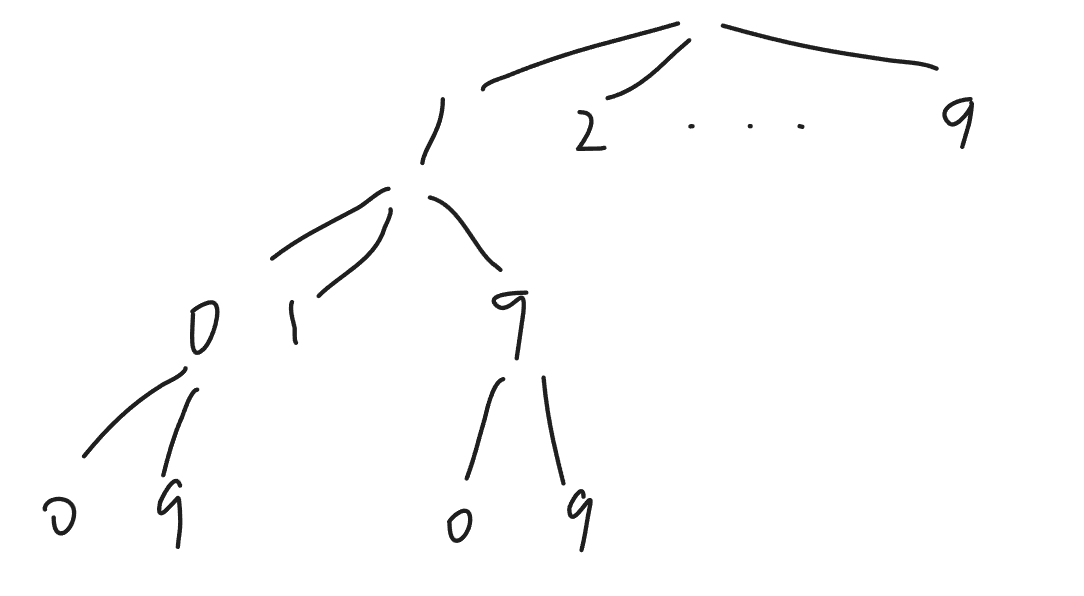
题目要求O(n)时间且不能用额外空间，因此就像440题那样，想象在一棵十叉树(十个孩子节点为0到9)上前序遍历，首先尽可能地乘10，这样字典序更小，如果超了就除以10，然后往右走，即加一。需要注意的是，当遍历到以9结尾的数时，要回溯到尾数没有9的祖先节点上，例如109需要回到10，然后往右到11；19和199都需要回到1，然后往右遍历到2。这也是内层while循环的原因。

代码

class Solution {
    public List<Integer> lexicalOrder(int n) {
        List<Integer> ans = new ArrayList<>();
        int p = 1;
        int k = 0;
        while (k < n) {
            if (p <= n) {
                ans.add(p);
                p *= 10;
                k++;
            } else {
                p /= 10;
                while (p % 10 == 9) {
                    p /= 10;
                }
                p++;
            }
        }
        return ans;
    }
}