1039. 多边形三角剖分的最低得分

题目

你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。

假设将多边形 剖分 为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回 多边形进行三角剖分后可以得到的最低分 。

示例 1：

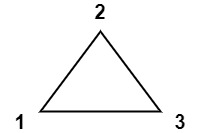
输入：values = [1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

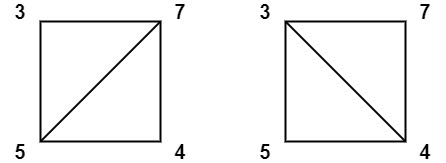
输入：values = [3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：。最低分数为 144。

示例 3：

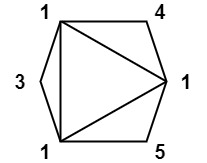
输入：values = [1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 。

提示：

n == values.length
3 <= n <= 50
1 <= values[i] <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-score-triangulation-of-polygon
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

时隔一年确实忘了，就和做新题一样…因为去年就没做出来吧，这次也是没想到应该用动态规划…

状态定义： 表示数组区间内剖分三角形的最小分数

状态转移方程：%2C%20i%20%3C%20k%20%3C%20j%2C%20%20j%20-%20i%20%3E%3D%202#card=math&code=dp%5Bi%5D%5Bj%5D%20%3D%20min%28dp%20%5Bi%5D%20%5Bk%5D%20%2B%20dp%20%5Bk%5D%20%5Bj%5D%20%2B%20values%5Bi%5D%20%2A%20values%5Bk%5D%20%2A%20values%5Bj%5D%29%2C%20i%20%3C%20k%20%3C%20j%2C%20%20j%20-%20i%20%3E%3D%202&id=v3t5Z)

二维数组对应的矩阵最终要求右上角值，长度为时，对应下图。需要填充的为带*的位置。遍历时从最下面开始，每一行从左往右，因此需要从大值开始，从小值开始。

   0 1 2 3 4
0      * * *
1        * *
2          *
3        
4

另外，巧妙的是，当 时，默认的 是合理的。因此不需要单独初始化。

代码

class Solution {
    public int minScoreTriangulation(int[] values) {
        int n = values.length;
        int[][] dp = new int[n][n];
        for (int i = n - 1; i >= 0; i--) {
            for (int j = i + 2; j < n; j++) {
                dp[i][j] = Integer.MAX_VALUE;
                for (int k = i + 1; k < j; k++) {
                    dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j] + values[i] * values[k] * values[j]);
                }
            }
        }
        return dp[0][n - 1];
    }
}