378. 有序矩阵中第 K 小的元素

题目

给你一个 n x n 矩阵 matrix ，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。
请注意，它是 排序后 的第 k 小元素，而不是第 k 个 不同 的元素。

你必须找到一个内存复杂度优于 O(n^2) 的解决方案。

示例 1：

输入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出：13
解释：矩阵中的元素为 [1,5,9,10,11,12,13,13,15]，第 8 小元素是 13

示例 2：

输入：matrix = [[-5]], k = 1
输出：-5

提示：

n == matrix.length
n == matrix[i].length
1 <= n <= 300
-10^9 <= matrix[i][j] <= 10^9
题目数据 保证 matrix 中的所有行和列都按 非递减顺序 排列
1 <= k <= n^2

进阶：

你能否用一个恒定的内存(即 O(1) 内存复杂度)来解决这个问题?
你能在 O(n) 的时间复杂度下解决这个问题吗?这个方法对于面试来说可能太超前了，但是你会发现阅读这篇文章（ this paper ）很有趣。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/kth-smallest-element-in-a-sorted-matrix
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

从今天的每日一题「668. 乘法表中第k小的数」过来的，复习一下。

「官解」的二分思路，利用到了矩阵每一行每一列都是递增的性质。

矩阵左上角为最小的数，右下角为最大的数，二分中间的数mid，可以在O(n)时间内求出小于等于mid的个数。

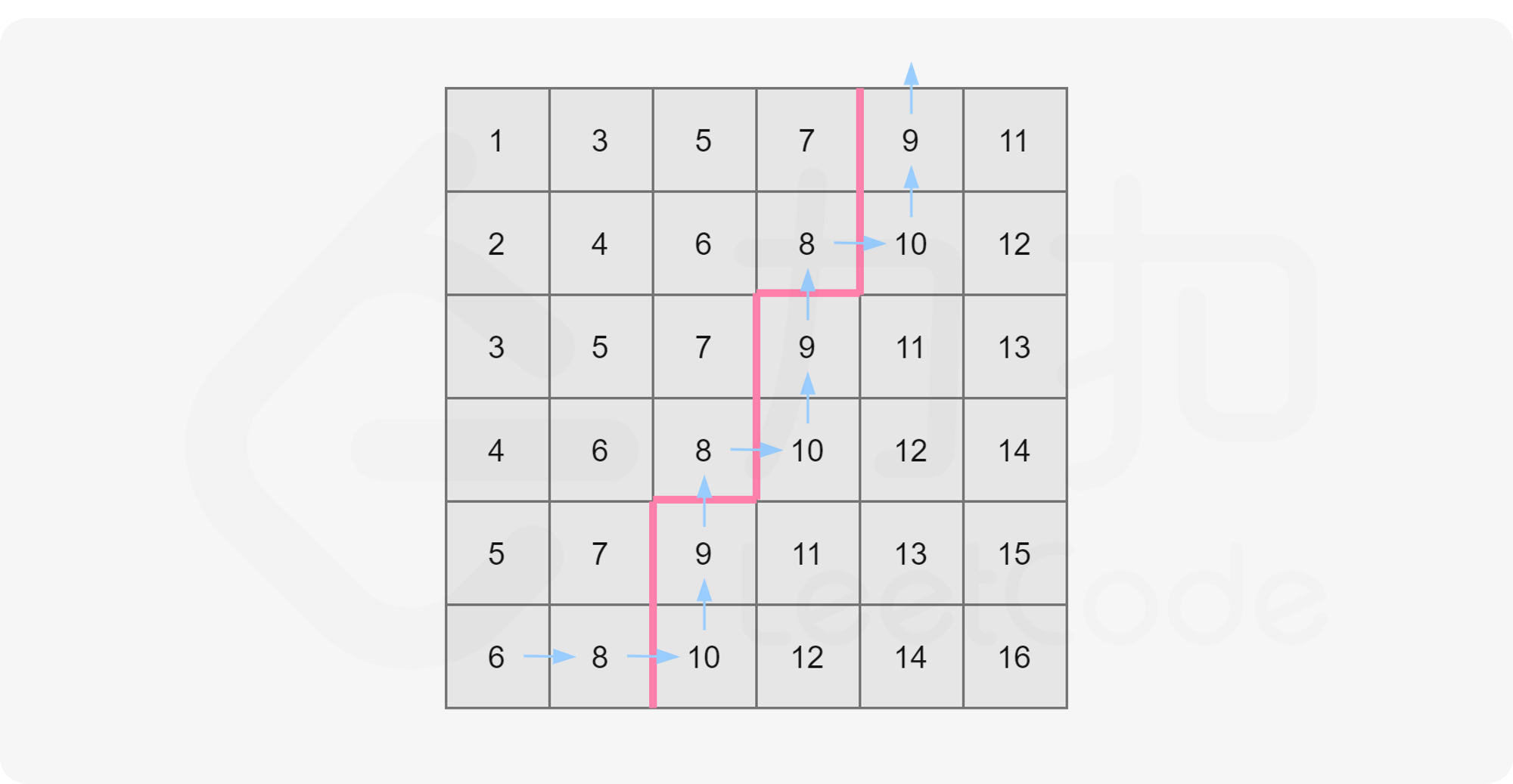
就像下图（图片引自自官解题解），求小于等于8的数目，从左下角开始，先在当前行「向右」找到第一个大于8的数，然后「向上」，再向右找第一个大于8的数，每一行都同理，可以发现，路径一定是向上和向右的，最多走2n步即可到达右上角。每一行找到的数的下标即是当前行小于等于8的个数。

如果小于等于8的数目小于k，说明8比第k个数小了，在大的数中继续二分，否则在另一边二分。

代码

class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        int n = matrix.length;
        int left = matrix[0][0];
        int right = matrix[n - 1][n - 1];
        while (left < right) {
            int mid = left + (right - left) / 2;
            int cnt = calSmaller(mid, matrix, n);
            if (cnt < k) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return left;
    }
    // 统计matrix中不大于num的数的个数
    private int calSmaller(int num, int[][] matrix, int n) {
        int row = n - 1;
        int col = 0;
        int cnt = 0;
        while (row >= 0) {
            while (col < n && matrix[row][col] <= num) {
                col++;
            }
            cnt += col;
            row--;
        }
        return cnt;
    }
}