973. 最接近原点的 K 个点

题目

给定一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点，并且是一个整数 k ，返回离原点 (0,0) 最近的 k 个点。

这里，平面上两点之间的距离是 欧几里德距离（ √(x1 - x2)2 + (y1 - y2)2 ）。

你可以按 任何顺序 返回答案。除了点坐标的顺序之外，答案 确保 是 唯一 的。

示例 1：

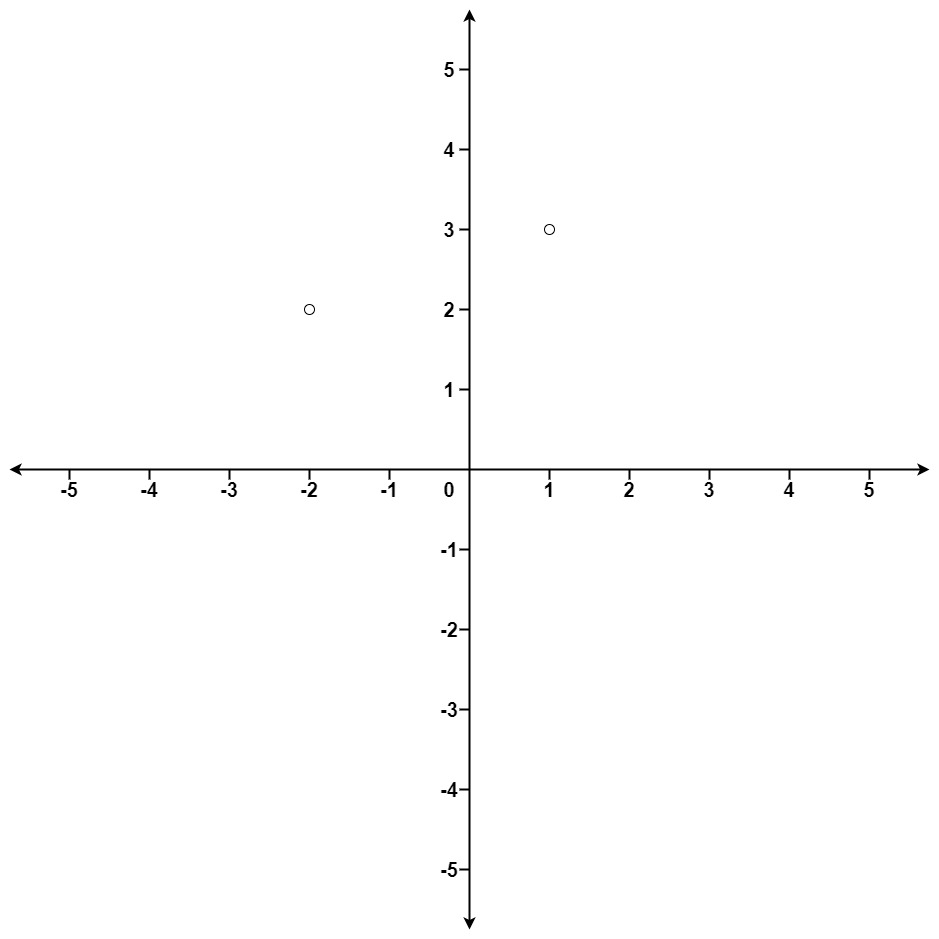
输入：points = [[1,3],[-2,2]], k = 1
输出：[[-2,2]]
解释：
(1, 3) 和原点之间的距离为 sqrt(10)，
(-2, 2) 和原点之间的距离为 sqrt(8)，
由于 sqrt(8) < sqrt(10)，(-2, 2) 离原点更近。
我们只需要距离原点最近的 K = 1 个点，所以答案就是 [[-2,2]]。

示例 2：

输入：points = [[3,3],[5,-1],[-2,4]], k = 2
输出：[[3,3],[-2,4]]
（答案 [[-2,4],[3,3]] 也会被接受。）

提示：

1 <= k <= points.length <= 10^4
-10^4 < xi, yi < 10^4

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/k-closest-points-to-origin
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

经典的问题，一般有优先队列和快排两种解法。

代码

优先队列

其实优先队列大小为就够了，下面的写法是比较省事

class Solution {
    public int[][] kClosest(int[][] points, int K) {
        int[][] ans = new int[K][2];
        // 这里使用小顶堆，如果大小设置为K需要换成大顶堆
        PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b) -> a[0] * a[0] + a[1] * a[1] - b[0] * b[0] - b[1] * b[1]);
        for (int[] p : points) {
            minHeap.offer(p);
        }
        for (int i = 0; i < K; i++) {
            ans[i] = minHeap.poll();
        }
        return ans;
    }
}

快排

同题写法差不多，基本就是一个标准的快排模板。不同的是这里排序的是二维数组，排序的标准是欧几里德距离。

class Solution {
    public int[][] kClosest(int[][] points, int K) {
        qSort(points, 0, points.length - 1, K);
        int[][] ans = new int[K][2];
        for (int i = 0; i < K; i++) {
            ans[i] = points[i];
        }
        return ans;
    }
    private void qSort(int[][] points, int p, int r, int k) {
        int q = partition(points, p, r);
        // q为下标，从0开始，因此和k存在一个偏差
        if (q == k - 1) {
            return;
        }
        if (q > k - 1) {
            qSort(points, p, q - 1, k);
        } else {
            qSort(points, q + 1, r, k);
        }
    }
    private int partition(int[][] points, int p, int r) {
        int pivot = dist(points[r]);
        int i = p;
        for (int j = p; j < r; j++) {
            if (dist(points[j]) < pivot) {
                swap(points, i, j);
                i++;
            }
        }
        swap(points, i, r);
        return i;
    }
    private void swap(int[][] points, int i, int j) {
        int[] tmp = points[i];
        points[i] = points[j];
        points[j] = tmp;
    }
    private int dist(int[] p) {
        return p[0] * p[0] + p[1] * p[1];
    }
}