题目

给你一棵 树（即一个连通、无向、无环图），根节点是节点 0 ，这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树，其中 parent[i] 是节点 i 的父节点，由于节点 0 是根节点，所以 parent[0] == -1 。

另给你一个字符串 s ，长度也是 n ，其中 s[i] 表示分配给节点 i 的字符。

请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ，并返回该路径的长度。

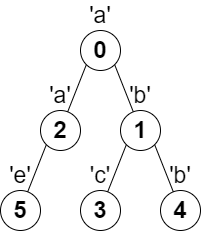
示例 1： image.png

输入：parent = [-1,0,0,1,1,2], s = “abacbe”
输出：3
解释：任意一对相邻节点字符都不同的最长路径是：0 -> 1 -> 3 。该路径的长度是 3 ，所以返回 3 。
可以证明不存在满足上述条件且比 3 更长的路径。

示例 2：

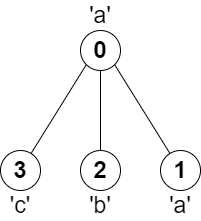
image.png

输入：parent = [-1,0,0,0], s = “aabc”
输出：3
解释：任意一对相邻节点字符都不同的最长路径是：2 -> 0 -> 3 。该路径的长度为 3 ，所以返回 3 。

提示：

n == parent.length == s.length
1 <= n <= 10^5
对所有 i >= 1 ，0 <= parent[i] <= n - 1 均成立
parent[0] == -1
parent 表示一棵有效的树
s 仅由小写英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-path-with-different-adjacent-characters
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

类似687题，和687不同的是，这道是多叉树，这道是不同的值可以形成路径，最后，这道求的是点的数目不是边。

首先，需要先自己构造树，然后同样使用dfs进行后序遍历，大体代码框架和687相同。

需要注意的是，因为这个题是多叉树，一个点纳入最终的路径最多有两个分支，因此需要记录节点所有孩子子树中最大的两个返回值。

代码

  1. class Solution {
  2.     int ans = 1;
  4.     public int longestPath(int[] parent, String s) {
  5.         int n = parent.length;
  6.         List<Integer>[] adjs = new ArrayList[n];
  7.         for (int i = 0; i < n; i++) {
  8.             adjs[i] = new ArrayList<>();
  9.         }
  10.         for (int i = 1; i < n; i++) {
  11.             adjs[parent[i]].add(i);
  12.         }
  13.         dfs(adjs, 0, s, 'a');
  14.         return ans;
  15.     }
  17.     // 函数返回以root为根的子树的最长的一条路径的长度(长度算的是节点数目)
  18.     // 对「一条路径」的理解：root每一层只能有一个节点包含在路径中
  19.     private int dfs(List<Integer>[] adjs, int root, String s, char c) {
  20.         // root的孩子节点的dfs返回值中的最大值
  21.         int a = 0;
  22.         // root的孩子节点的dfs返回值中的第二大值
  23.         int b = 0;
  24.         for (int child : adjs[root]) {
  25.             int k = dfs(adjs, child, s, s.charAt(root));
  26.             if (k >= a) {
  27.                 // 记得先把最大值赋给次大值
  28.                 b = a;
  29.                 a = k;
  30.             } else if (k > b) {
  31.                 b = k;
  32.             }
  33.         }
  34.         // 这里不同于687，求的是点的数目，因此+1
  35.         // 1的含义是root节点本身算作一个节点，再加上其左右子树中最长的两条路径a和b(都是节点数)
  36.         ans = Math.max(ans, a + b + 1);
  37.         // root处的字符和其父节点不同，就可以将root节点算到路径中一个，对应下面的+1，否则整棵root子树的节点都不能算，对父节点的贡献就是0
  38.         return s.charAt(root) != c ? a + 1 : 0;
  39.     }
  40. }