337. 打家劫舍 III

题目

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

示例 1:

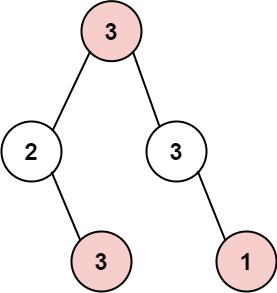
输入: root = [3,2,3,null,3,null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

示例 2:

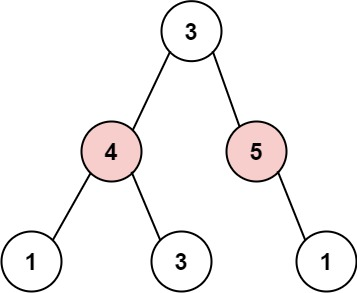
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

提示：

树的节点数在 [1, 10^4] 范围内
0 <= Node.val <= 10^4

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/house-robber-iii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

对于root，可以偷也可以不偷，最终返回两者的较大者。代码中对应主函数部分。因此增加一个辅助函数dfs计算对于root节点，偷和不偷分别获得的最大值，返回一个长度为2的数组。dfs实现细则见注释。

代码

class Solution {
    public int rob(TreeNode root) {
        int[] res = dfs(root);
        return Math.max(res[0], res[1]);
    }
    // 对于root，可以偷也可以不偷，选择偷的最大值为res[1]，不偷的最大值为res[0]
    private int[] dfs(TreeNode root) {
        int[] res = new int[2];
        if (root == null) {
            return res;
        }
        int[] left = dfs(root.left);
        int[] right = dfs(root.right);
        // 选择不偷root的话，最大金额为左子树最大金额加右子树最大金额，对于左子树是max(left[0],left[1])，右子树也一样
        res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        // 选择偷root的话，左右子树都不能偷，left[0]+right[0]再加上root.val
        res[1] = root.val + left[0] + right[0];
        return res;
    }
}