2049. 统计最高分的节点数目

题目

给你一棵根节点为 0 的 二叉树 ，它总共有 n 个节点，节点编号为 0 到 n - 1 。同时给你一个下标从 0 开始的整数数组 parents 表示这棵树，其中 parents[i] 是节点 i 的父节点。由于节点 0 是根，所以 parents[0] == -1 。

一个子树的 大小 为这个子树内节点的数目。每个节点都有一个与之关联的 分数 。求出某个节点分数的方法是，将这个节点和与它相连的边全部 删除 ，剩余部分是若干个 非空 子树，这个节点的 分数 为所有这些子树 大小的乘积 。

请你返回有 最高得分 节点的 数目 。

示例 1:

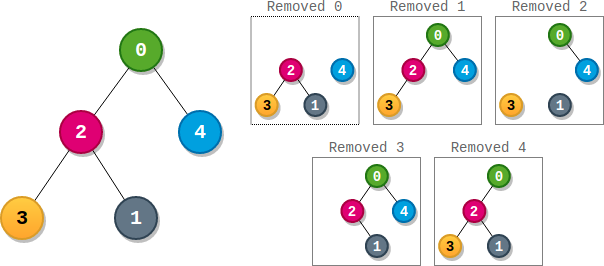
输入：parents = [-1,2,0,2,0]
输出：3
解释：

• 节点 0 的分数为：3 * 1 = 3
• 节点 1 的分数为：4 = 4
• 节点 2 的分数为：1 1 2 = 2
• 节点 3 的分数为：4 = 4
• 节点 4 的分数为：4 = 4
  最高得分为 4 ，有三个节点得分为 4 （分别是节点 1，3 和 4 ）。

示例 2：

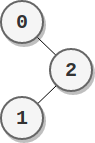
输入：parents = [-1,2,0]
输出：2
解释：

• 节点 0 的分数为：2 = 2
• 节点 1 的分数为：2 = 2
• 节点 2 的分数为：1 * 1 = 1
  最高分数为 2 ，有两个节点分数为 2 （分别为节点 0 和 1 ）。

提示：

n == parents.length
2 <= n <= 10^5
parents[0] == -1
对于 i != 0 ，有 0 <= parents[i] <= n - 1
parents 表示一棵二叉树。

思路

这是很有意思、很值得回看的一道题，想写出优雅的DFS要下功夫呀。

思路首先是通过数组构造出树来，这里的树其实不关注节点的值，只关注个数，关注一个节点左子树的节点个数和右子树的节点个数。知道了这两个值便可以计算出一个节点的分数。那么我们先用求出每个子树的节点个数，存放在中，之后求分数就可以用了。这样只需要深搜一遍树。

进一步解释在注释里。

代码

class Solution {
    public int countHighestScoreNodes(int[] parents) {
        int n = parents.length;
        int[] nodeNum = new int[n];
        // 构造树，存放每个节点的孩子节点
        // 值得注意的是，不需要在意孩子节点顺序和值，循环的写法也也可以直接推广到N叉树
        List<Integer>[] child = new List[n];
        for (int i = 0; i < n; i++) {
            child[i] = new ArrayList<>();
        }
        for (int i = 1; i < n; i++) {
            child[parents[i]].add(i);
        }
        // 先求出每个子树的节点个数，存放在nodeNum中
        dfs(0, child, nodeNum);
        int ans = 0;
        long max = 0;
        // 计算每个节点的分数
        for (int i = 0; i < n; i++) {
            // left表示当前节点左子树的节点数目，有可能没有左子树，但因为要算乘积，所以最小也是1，right同理
            int left = 1;
            int right = 1;
            // 有最少一个孩子，更新left
            if (child[i].size() >= 1) {
                left = nodeNum[child[i].get(0)];
            }
            // 有两个孩子，更新right
            if (child[i].size() == 2) {
                right = nodeNum[child[i].get(1)];
            }
            // 计算乘积，n-nodeNum[i]表示除了当前节点子树剩下的节点个数，注意这里不等效于n-left-right-1
            long product = (long) left * right * Math.max(n - nodeNum[i], 1);
            if (product == max) {
                ans++;
            } else if (product > max) {
                max = product;
                ans = 1;
            }
        }
        return ans;
    }
    private int dfs(int root, List<Integer>[] child, int[] nodeNum) {
        if (nodeNum[root] > 0) {
            return nodeNum[root];
        }
        int cnt = 1;
        for (int ch : child[root]) {
            cnt += dfs(ch, child, nodeNum);
        }
        nodeNum[root] = cnt;
        return cnt;
    }
}

看了官解，原来可以只深搜一次，统计子树节点个数的同时，计算分数，真是优雅，学习了。

class Solution {
    long maxProduct = 0;
    int ans = 0;
    public int countHighestScoreNodes(int[] parents) {
        int n = parents.length;
        List<Integer>[] child = new List[n];
        for (int i = 0; i < n; i++) {
            child[i] = new ArrayList<>();
        }
        for (int i = 1; i < n; i++) {
            child[parents[i]].add(i);
        }
        dfs(0, n, child);
        return ans;
    }
    private int dfs(int root, int n, List<Integer>[] child) {
        int size = n - 1;
        long product = 1;
        for (int ch : child[root]) {
            int c = dfs(ch, n, child);
            product *= c;
            size -= c;
        }
        if (root != 0) {
            product *= size;
        }
        if (product == maxProduct) {
            ans++;
        } else if (product > maxProduct) {
            maxProduct = product;
            ans = 1;
        }
        return n - size;
    }
}