1601. 最多可达成的换楼请求数目

题目

我们有 n 栋楼，编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节，部分员工想要换一栋楼居住。

给你一个数组 requests ，其中 requests[i] = [fromi, toi] ，表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。

一开始 所有楼都是满的，所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ，一个员工要离开楼 1 ，一个员工要离开楼 2 ，如果该请求列表可行，应该要有两个员工搬入楼 0 ，一个员工搬入楼 1 ，一个员工搬入楼 2 。

请你从原请求列表中选出若干个请求，使得它们是一个可行的请求列表，并返回所有可行列表中最大请求数目。

示例 1：

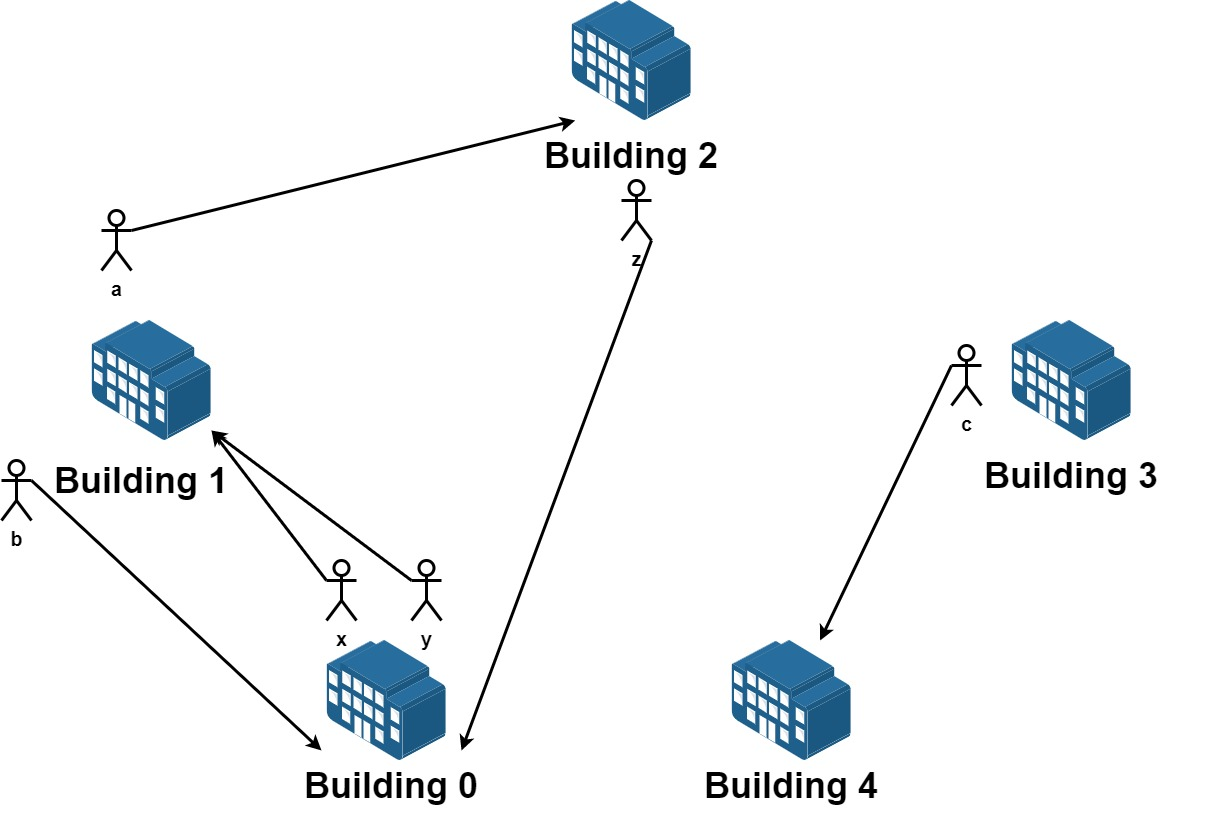
输入：n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出：5
解释：请求列表如下：
从楼 0 离开的员工为 x 和 y ，且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ，且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ，且他想要搬到楼 0 。
从楼 3 离开的员工为 c ，且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼，以满足他们的请求。
我们可以让 y，a 和 z 三人在三栋楼间交换位置，满足他们的要求。
所以最多可以满足 5 个请求。

示例 2： 输入：n = 3, requests = [[0,0],[1,2],[2,1]]
输出：3
解释：请求列表如下：
从楼 0 离开的员工为 x ，且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ，且他想要搬到楼 2 。
从楼 2 离开的员工为 z ，且他想要搬到楼 1 。
我们可以满足所有的请求。

提示： 1 <= n <= 20
1 <= requests.length <= 16
requests[i].length == 2
0 <= fromi, toi < n

思路

题意比较容易理解，一看和长度的范围就知道一定需要暴力枚举，复杂度在指数量级。

我们依次遍历中的每一个请求，分别满足和不满足其的情况，当遍历完后，查看是否满足题意“所有楼的人数不变”，这里用一个数组diff记录人数的变化，离开一个人减一，搬入一个人加一，如果最后数组全是，则满足题意。这里可以不用最后专门遍历，可以在更新的同时维护一个变量，记录中的个数。另外，需要维护一个变量，记录满足的请求数，每次遍历完一个分支，将和比较更新一下。

代码

回溯

class Solution {
    int ans = 0;
    public int maximumRequests(int n, int[][] requests) {
        int[] diff = new int[n];
        dfs(0, n, requests, diff, n, 0);
        return ans;
    }
    private void dfs(int k, int n, int[][] requests, int[] diff, int zero, int cnt) {
        if (k == requests.length) {
            if (zero == n) {
                ans = Math.max(ans, cnt);
            }
            return;
        }
        // 不满足第k个请求
        dfs(k + 1, n, requests, diff, zero, cnt);
        // 满足第k个请求
        // 离开requests[k][0]楼
        // 更新diff之前之后都需要维护一下zero变量
        if (diff[requests[k][0]] == 0) {
            zero--;
        }
        diff[requests[k][0]]--;
        if (diff[requests[k][0]] == 0) {
            zero++;
        }
        if (diff[requests[k][1]] == 0) {
            zero--;
        }
        diff[requests[k][1]]++;
        if (diff[requests[k][1]] == 0) {
            zero++;
        }
        dfs(k + 1, n, requests, diff, zero, cnt + 1);
        // 状态重置 撤回对diff的更新
        diff[requests[k][0]]++;
        diff[requests[k][1]]--;
    }
}

二进制枚举

这类题一般也可以用二进制枚举的方式做，更好理解，代码也更简洁。记为，那么一共有种可能，可以用一个介于到之间的整数表示每一种情况，这其中的整数有个二进制位，第位表示第个请求是否得到满足，如果为表示满足，为不满足。

class Solution {
    public int maximumRequests(int n, int[][] requests) {
        int ans = 0;
        int m = requests.length;
        int k = 1 << m;
        for (int i = 0; i < k; i++) {
            int cnt = 0;
            int[] diff = new int[n];
            for (int j = 0; j < m; j++) {
                if ((i >> j & 1) == 1) {
                    cnt++;
                    diff[requests[j][0]]--;
                    diff[requests[j][1]]++;
                }
            }
            boolean flag = true;
            for (int j = 0; j < n; j++) {
                if (diff[j] != 0) {
                    flag = false;
                    break;
                }
            }
            if (flag) {
                ans = Math.max(ans, cnt);
            }
        }
        return ans;
    }
}