产品上决定做子图嵌套是在 2021 年 1 月底，回想起来，当时做出这个决定还是比较纠结的。因为，产品上本就不是想做 XMind，也不想被 XMind 牵着走，更不想背包袱（有了 XMind 的功能，也意味着有了它的包袱）。但无奈的是，在面对一些具体场景时，当时没找到更合适的做法。最终还是硬着头皮上了，好在最终结果上看，我们虽然沿着 XMind 的路径，但貌似走出了一条也许比 XMind 更宽广的道路。

小溪鲨鱼

“很幸运，我们所在的这条小溪没有大鲨鱼，所以我们才能够这样活到现在，并且活得很好。才有时间去尝试更多的可能。” —— 来源《在 XMind 工作是怎样的体验？》

透过一些公开分享资料，会发现 XMind 的人喜欢用“小溪里没鲨鱼”，比喻在思维导图是个过于细分的领域，没有巨头进来，以至于他们这十几年，活下来了，且活的很好。

从某个角度来说这是对的，毕竟区区思维导图，如果巨头愿意投入足够的人力，是一定能做出来的。

从另一个角度看，这句话也是 XMind 谦虚的表现。因为十多年只做一件事，并把它做到世界第一，那这里面一定是有壁垒的。比如本篇提的子图嵌套，市面上林林总总的思维导图软件那么多，但实现这个功能的，只有寥寥几家。语雀思维图也是做了一年半，才走到这一步。所以这应该称不上是一件简单的事情。

还有，一方面，这次语雀思维图的子图嵌套，深受 XMind 的启发。另一方面，在图编排领域，思维导图是一个非常年轻子领域，作为一家民族企业，能秉持长期主义，持续投入，并这么多年来稳居世界第一，那还是蛮厉害的。向 XMind 致敬。

黑屋找门

古来，数学家在证明一个定理时，常常用黑屋找门比喻，自身处境艰难，比如：

“数学家就像身在一间黑屋里的盲人，努力想看清一只黑猫，而那只黑猫也许根本就不存在。”
—— 达尔文

“证明未知的猜想，就像在一个方圆 1 平方公里的黑屋子里找路，没有任何光亮。”
—— 陈秀雄

“解决费马大定理，就是要穿过一个一个的黑屋子，首先我来到一个黑屋子，什么都看不见。我先得去摸摸这个屋子里的所有家具，所有摆设，等摸得烂熟。对这个房间的每一个纹理都清楚的时候，我才能找到它的电灯开关。我打开电灯开关才能知道下一个屋子的门在哪。打开那个门，然后进入下一个屋子然后又开始这个过程。”
—— 安德鲁·怀尔斯

当然，子图嵌套的问题的难度远不及证明数学定理，笔者也没有傻到，要将自己和数学家类比。但在能力和问题难度大致相当的情况下，这种黑屋找门的感受是切实存在的。

在解决未知问题的过程中进错屋子是常态，进对屋子是巧合。由于笔者在解决这个问题的过程中，进错屋子太多，无法尽述。下面仅向大家分享，进对屋子的演绎链条。

黑屋 1：XMind 的方案真的足够好了吗？

XMind 的方案真的足够好了吗？在“暴力”试玩 XMind 后，我们发现 XMind 以下几种情况是不够好的：

显得有点诡异	图形有重叠，明显不够好	应该是 BUG 了

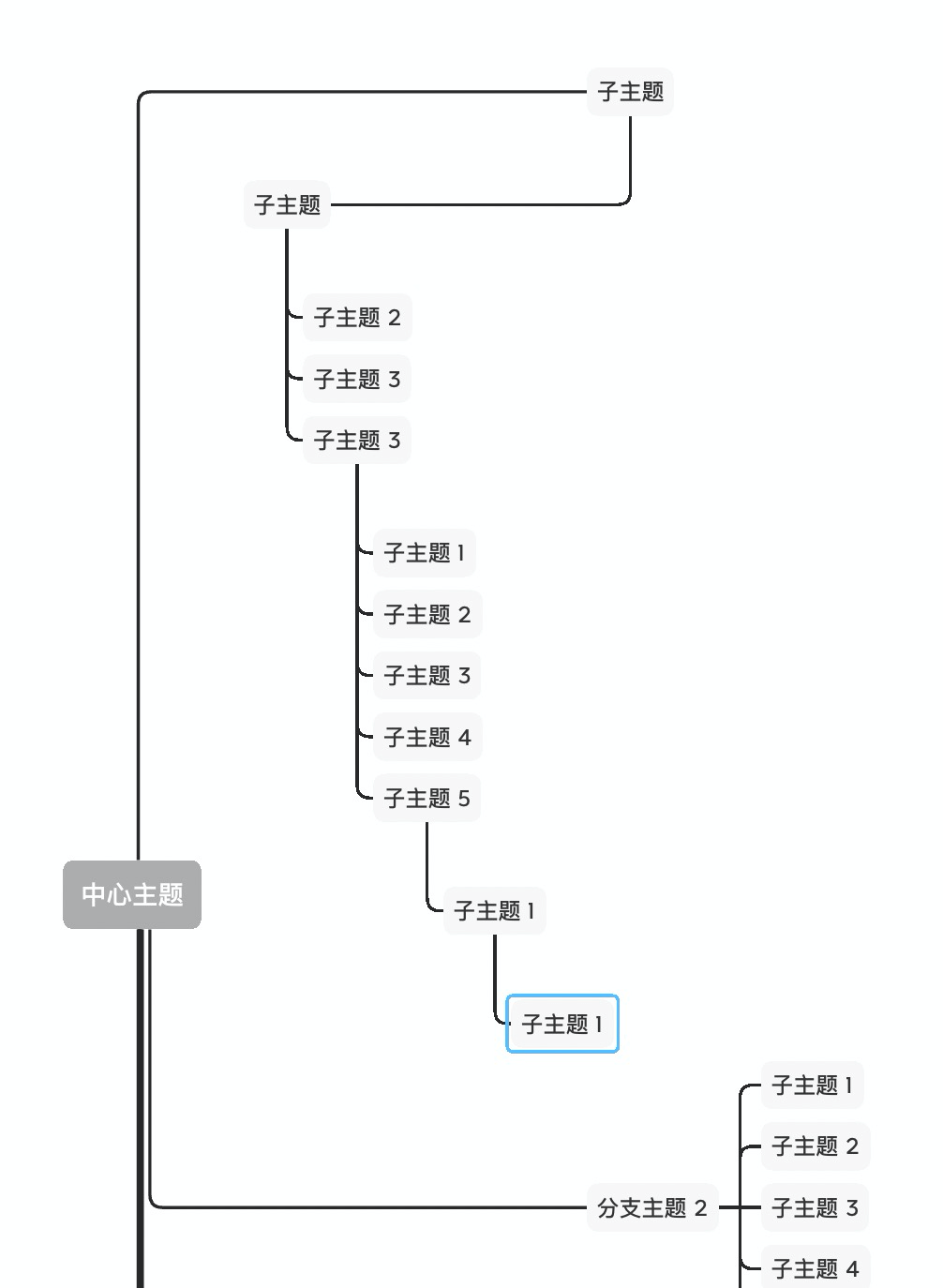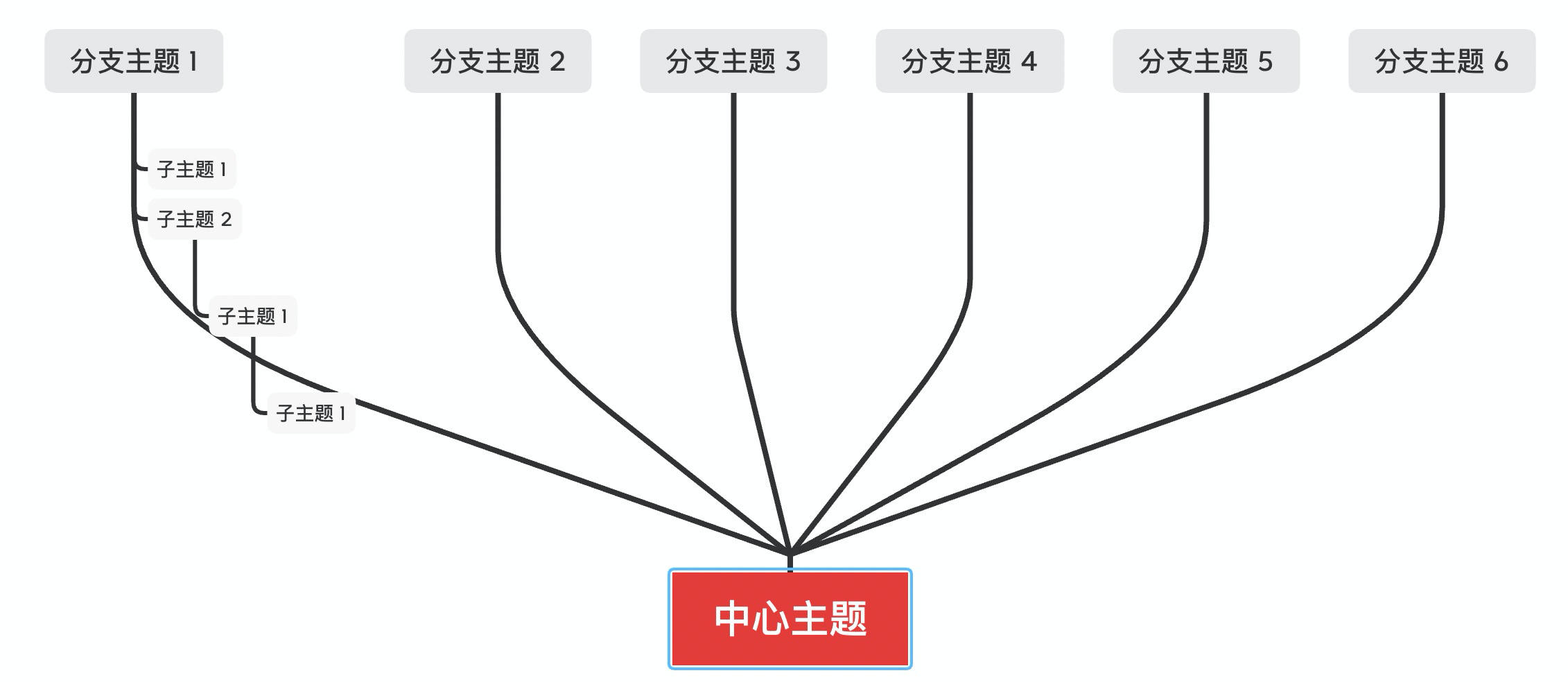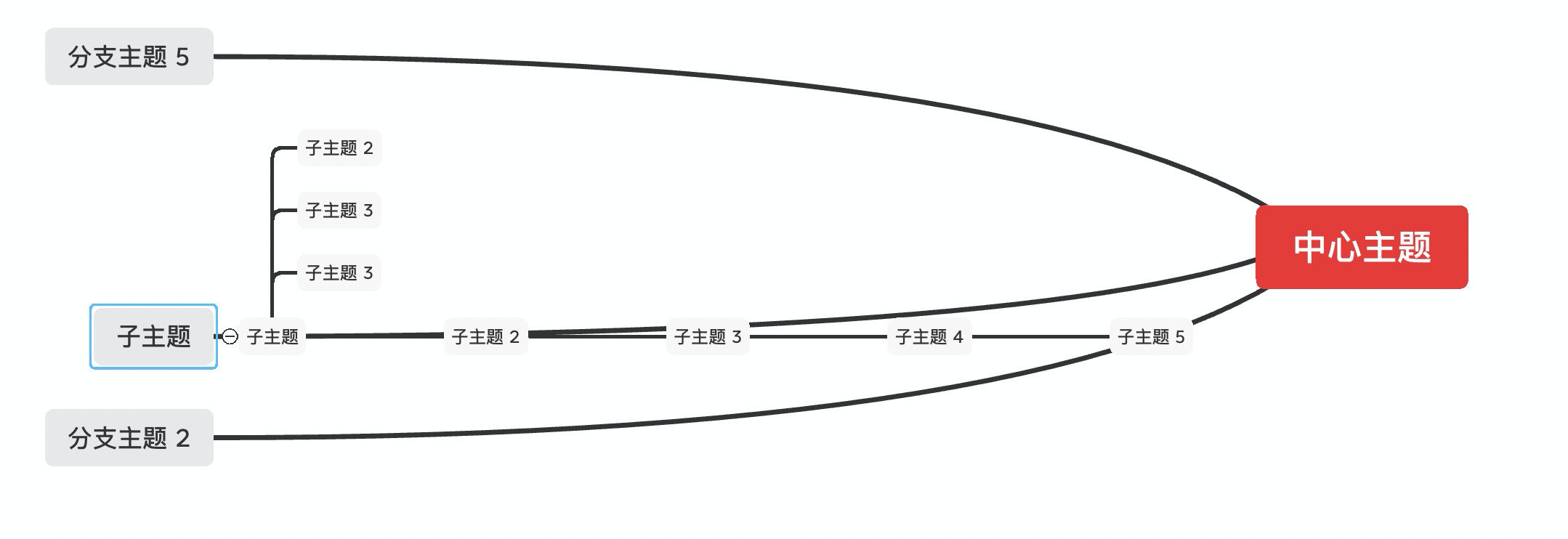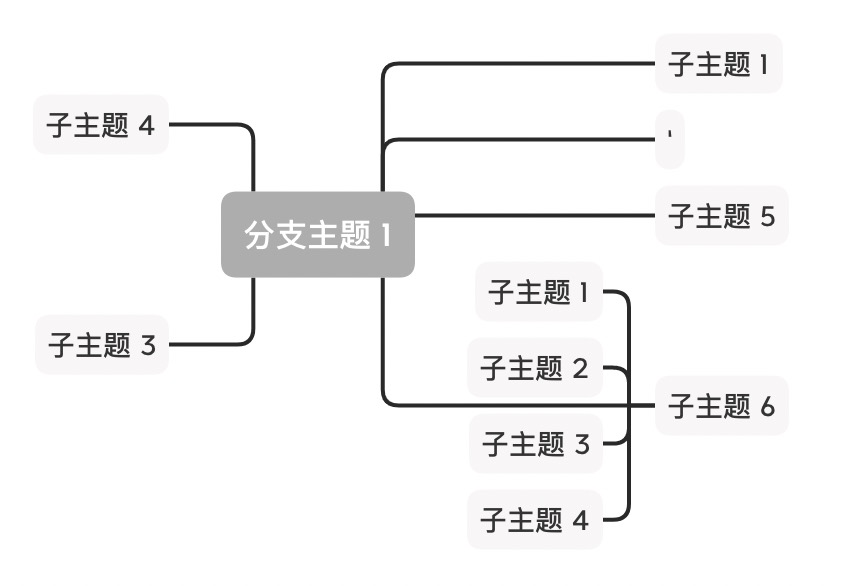如果别人的方案不够好，从产品设计上改如何改进？我们总结出一个设计原则：要限制可能产生冲突的组合。

那么如何定义冲突的组合呢？在产品设计，阶段大家使用的语言，可能是：“线不能重合”，“布局不能反向”，等。但从技术角度，我们此时离【如何定义冲突】这件屋子，之间还隔着好几个屋子。

黑屋 2：如何定义一个布局？

要讨论什么是思维导图布局的嵌套、布局的冲突，首先得讨论布局是什么。

思维导图，是一个树形分形（分形通常被定义为：一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状），就像雪花一样。这意味着纵使用户最终画出的图千千万万，但在定义算法时，只需要定义有限的几个。以目前结构举例：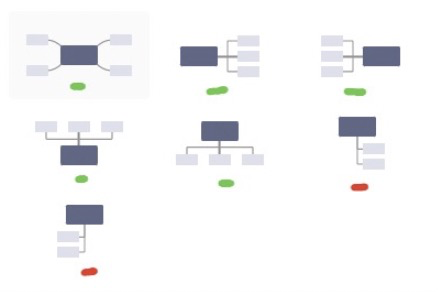

之前的 7 种结构中，只有两个布局算法，绿色和红色分别这两种布局算法衍生出的结构

在现有布局引擎里，要解释为什么一种布局算法，能衍生出多种布局，还需要引入额外一些概念，下面以标准布局（绿色集合）为例，引出算法、方向、象限，并逐个每个概念的定义及其作用。

类型 —— Type

类型是布局中的内核部分，它决定了整棵树的生长方式，上述三幅图分别对应了三种不同的布局算法。定义在节点上，约束其子节点。

方向 —— Direction

方向确定了算法的生长方向，上面四张图，分别属于同一种布局的四个方向。

象限 —— Quadrant

这个概念衍生自笛卡尔坐标系的四象限，放到布局这里比较晦涩。这里稍微花多点篇幅讲解其含义和作用。从定义上看，这里象限的含义还是空间的划分，是某空间的子空间，结合示例，具体解释如下：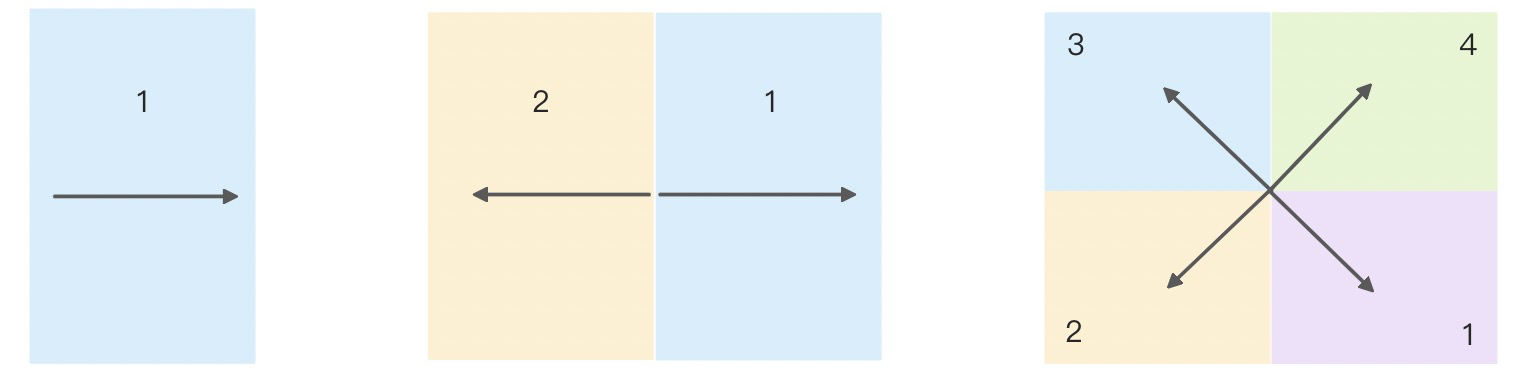

上图从左到右，分别是一个象限，两个象限，以及四个象限。象限的数量属于节点，在哪个象限展开（选择哪个象限），则由最近一级子节点决定。如何理解这句话？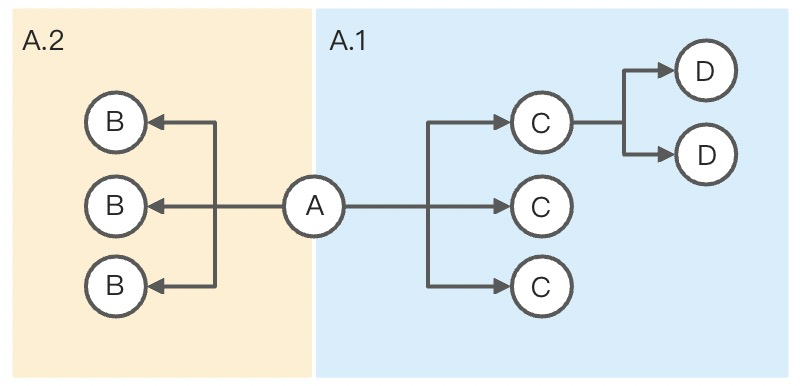

以上图举例，A 是含标准布局算法的节点，B、C、D 都是 A 的子节点，但只有 B、C 是其最近一级的子节点。象限的具体作用仅限于 A、B、C 具体表述为：节点 A 的象限数量为 2，B 在象限 A.2，C 在象限 A.1。

一句话描述，在实际编程中，象限的作用：通过影响布局算法的方向，以达到分配子树（图）的生长空间的目的。

黑屋 3：如何定义一个子图？

为便于叙述，先额为拓展一个概念：一个含布局的节点称之为核节点。

那么在本文中子图的概念是：若核节点 A 是核节点 B 的子节点，则称节点 A 及其子节点构成的图，是节点 B 的子图。

黑屋 4：基础的嵌套规则是什么？

这个看起来貌似是整个问题的核心，但科学的关键是证伪。有时候，是和不是相比是不值一文的。

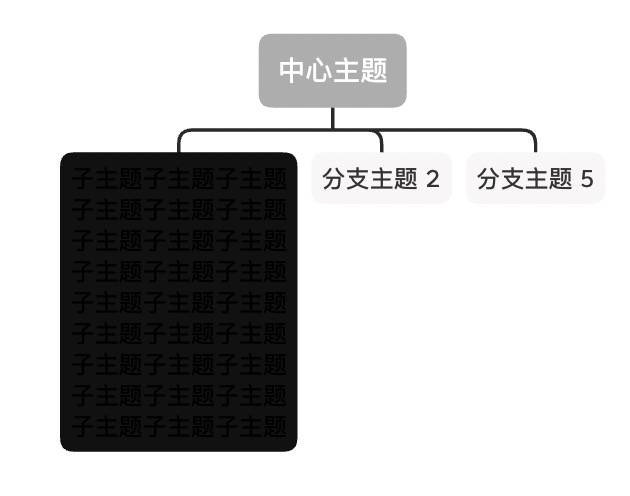
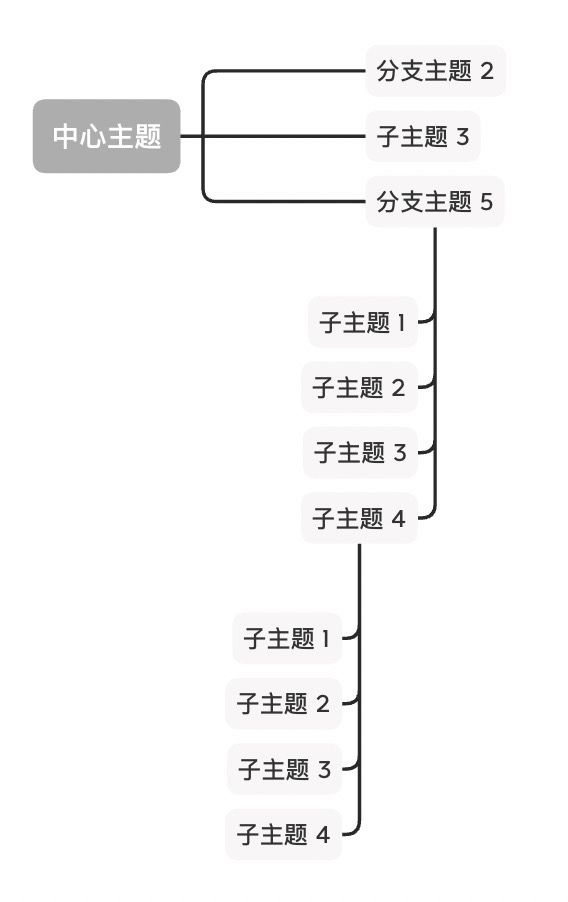
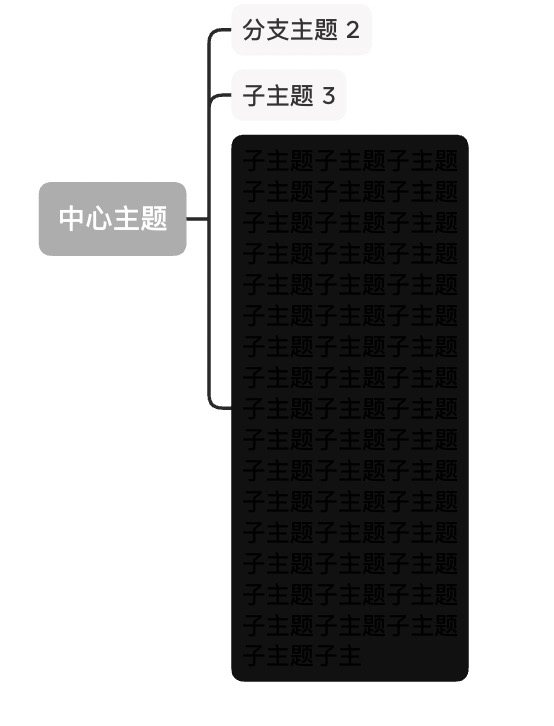
子图嵌套是个复杂的事情，为避免日后失控，导致这块成为成本中心。所以基础的嵌套我们追求一个极简的方案，一句话描述：将子图看成矩形黑盒。

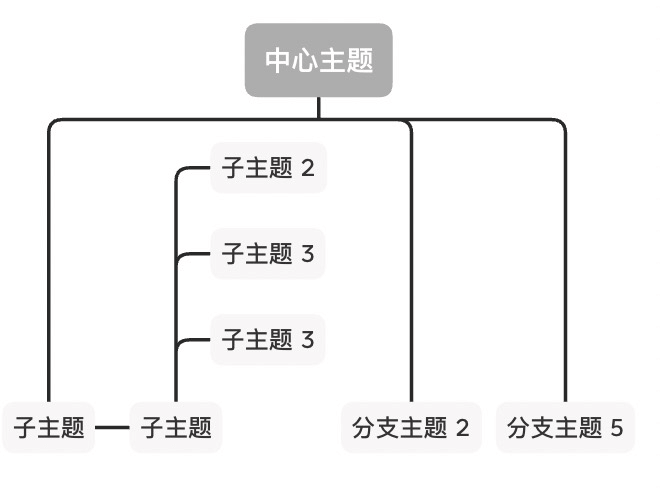
根据我们的规则，以下这些图预计会和 XMind 画的不一样。

XMind	YMind

黑屋 5：如何定义冲突？

这间屋子的结论很简单，但过程却比较曲折。爱思考的朋友，在看结论之前，不妨先自己思考一下。

先说结论：布局方向向量上，含有同向基向量，且不含反向基向量的布局，可以相互嵌套。

比较费解，展开解释一下。这里，我们不妨用一个向量来表示布局的方向，然后把问题归约到线性代数的领域去看。

那么什么是同向基向量？要理解这句话，首先需理解什么是基)（严格的定义点击链接去看，不再赘述）。由定义可知，两个线性无关的基可组成一个二维平面空间，在笛卡尔坐标系中，我们不妨找到一组基，分别是沿 x 轴的 (x, 0)，以及沿着 y 轴的 (0, y)。

由线性代数的相关的结论可知，任何一个空间中的任意向量，都能用基向量的线性组合表示。举例说明：
问： 分别与、、、 是否含有相同的基向量？

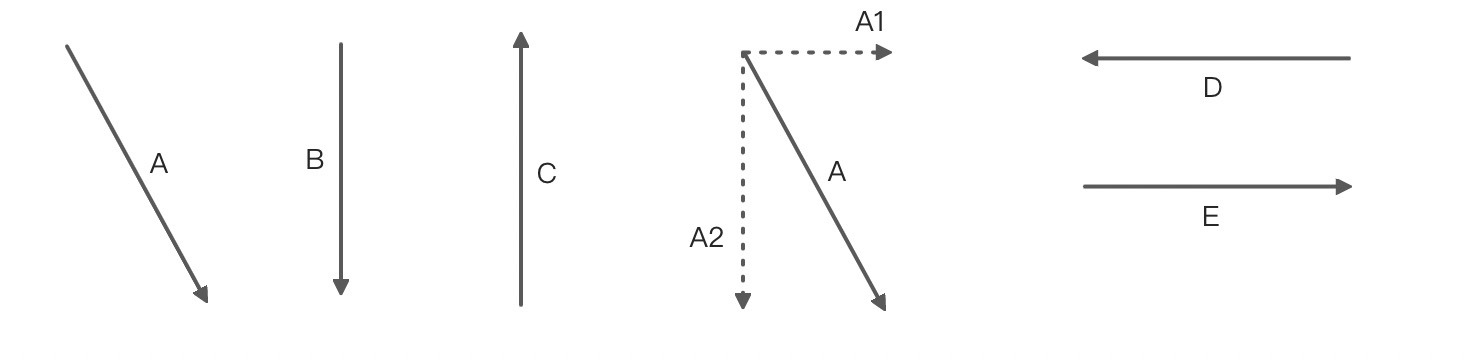
向量 由一组基向量 、 组成。那么由于分别有 和 ， 和 ，同向。所以有 和 ， 和 ，有同向基向量。反之 和 ， 和 ，没有同向基向量。

解释完同向基向量，回头再看如何理解这条规则。下面以缩进布局和标准布局的组合举例：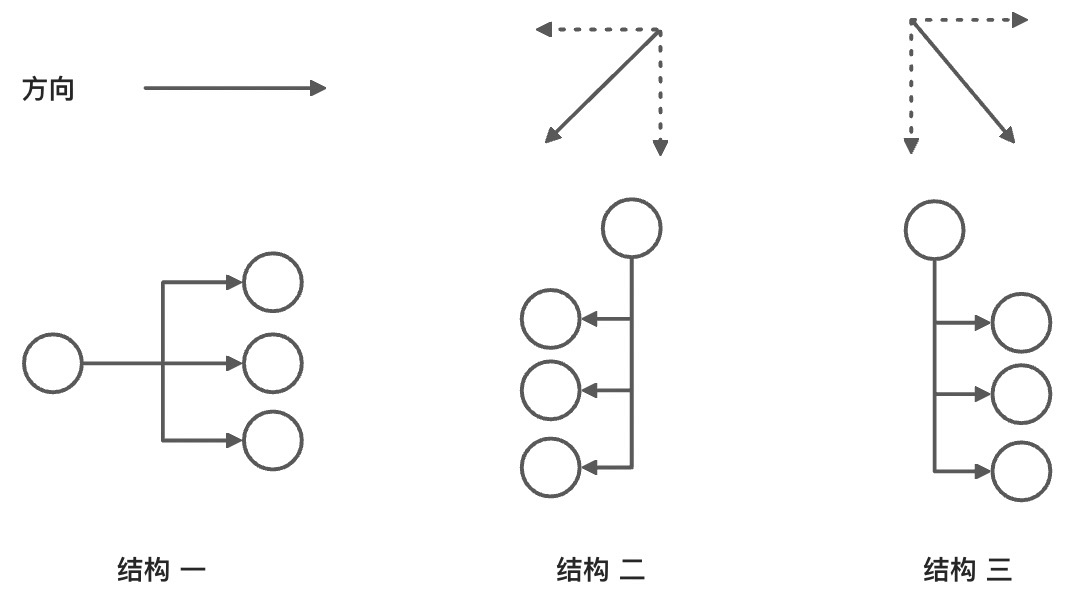

结构一和结构二没有同向基向量，所以不能互相嵌套。结构一和结构三，有同向的水平基向量，则可以相互嵌套。

在此规则下，无冲突的图形是：

上文黑屋 1 中提到的那些，则都存在冲突，到了这里，我们终于可以暂且回到第一个屋子，解释了什么是冲突。

黑屋 6：如何解决冲突？

虽说产品上的目标是避免冲突，但实际研发的过程中，真实的任务其实是解决冲突。这也是整套方案的核心，下面内容略费脑子，坐好扶稳了。

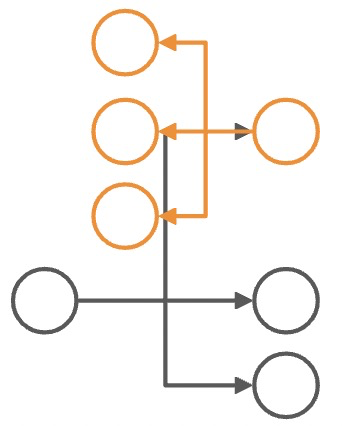
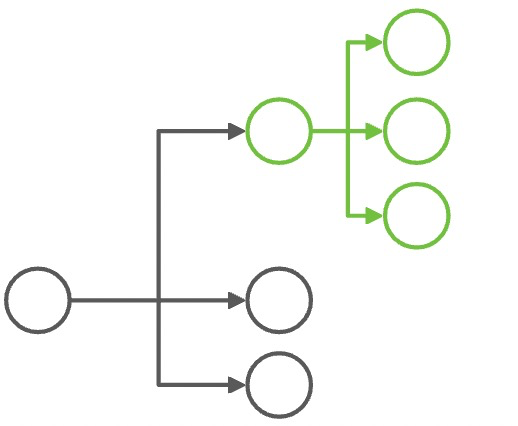
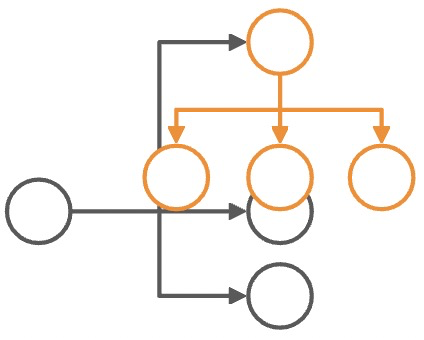
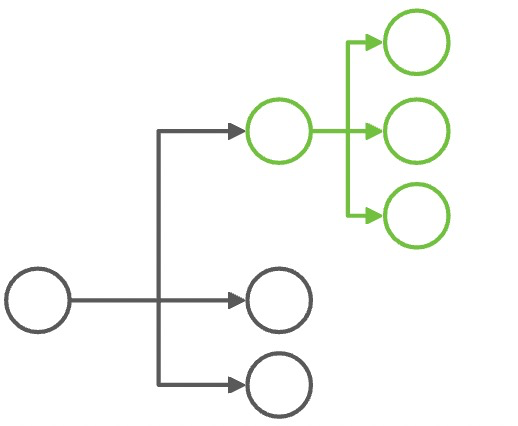
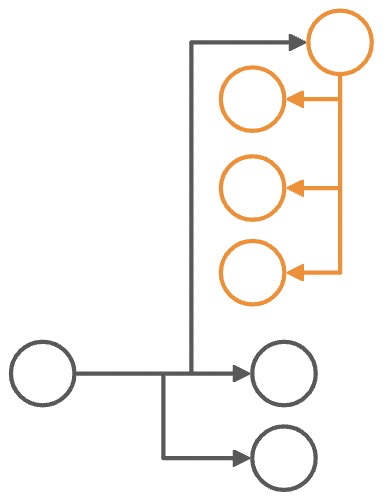
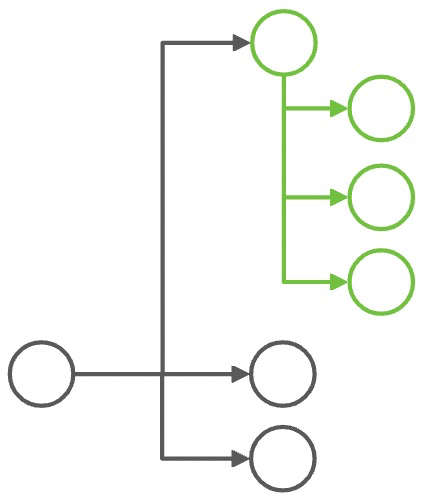
其实从最上层，case by case 去解冲突，其实每个问题看起来并不难，答案甚至是显而易见的。比如：

冲突组合	解决冲突
……	……

但这里我们从技术视角，这种排列组合是无法枚举，如果按穷举方式去做，未来一定是成本中心，因而我们有必要去构建一套理论，形成一个框架，去处理冲突。

概念补充

在正式进入之前，还需要补充一些概念。

如果觉得下文某些概念不清晰、缺漏、或是未使用业界标准用词。望指出，望斧正。

首先，在本次的方案中，对于一种布局来说，它的支持的方向和占满一个全空间所需象限数（后文简写：满象限数）是既定的。详解如下：

布局类型	布局方向	满象限数
标准布局（Standard）	4 [ 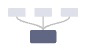, , 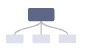, 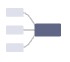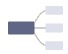]	2 [ , ]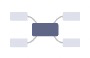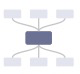
缩进布局（Intend）	4 [, , , ]	4 [ ]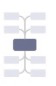

定义：实际可用象限数等于满象限数的布局，称之满布局。
根据该定义，进行一次拆解，能得到以下 3 个满布局：

编号	满布局	象限空间
m.1
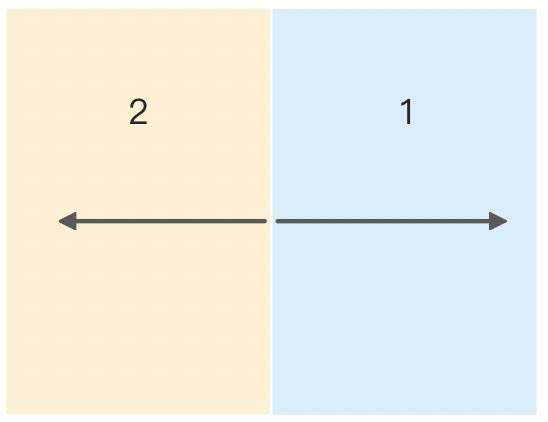m.2
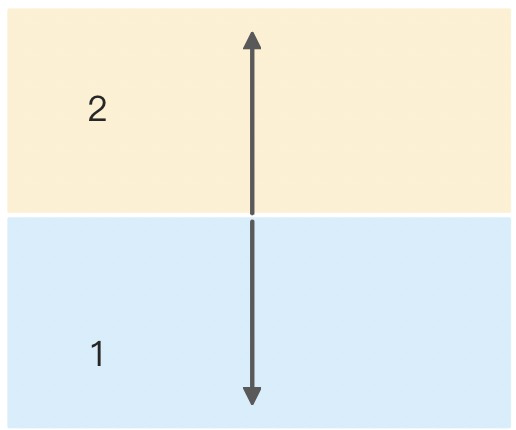m.3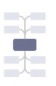

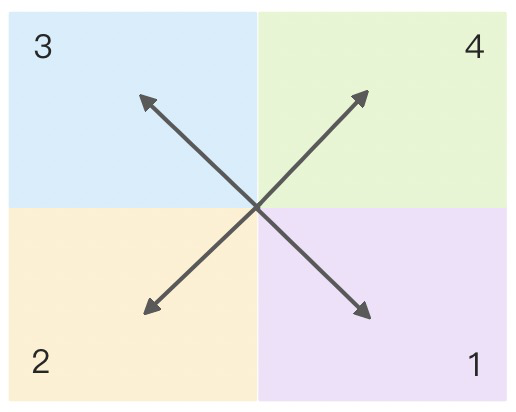定义：将子节点约束在某个象限下，我们称之为象限约束。
定义：满布局含象限约束得到的布局，称之缺布局。
进一步展开，有以下缺布局：

编号	对应满布局	布局	方向	约束象限
q.1	m.1		→	1
q.2	m.1		←	2
q.3	m.2		↓	1
q.4	m.2		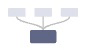↑	2
q.5	m.3		↘	1
q.6	m.3		↙	2
q.7	m.3		↖	3
q.8	m.3		↗	4

解决冲突

完成储备概念后，我们回来本节的主题，如何处理冲突？
先尝试将冲突大致分类：

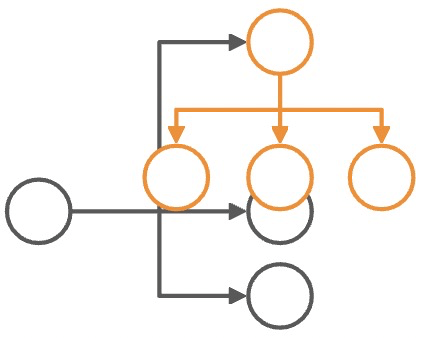
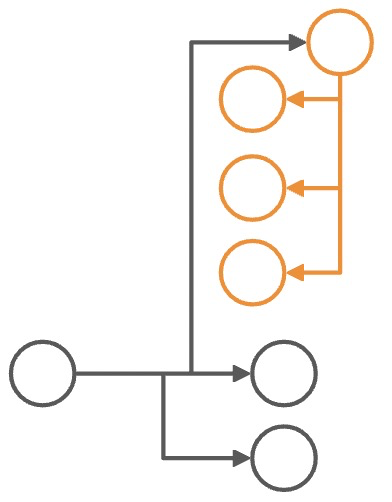
A：同类布局，相同满布局	B：同类布局，不同满布局	C：不同类布局

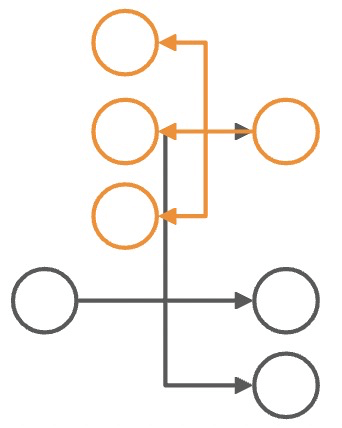经过审慎思考（此处省略 500 字），我们得出结论：

1. 对于含有相同方向的布局（比如：场景 A），只需要修改象限约束，得到无冲突的缺布局，即可解决冲突。
2. 若不含同向方向向量（比如：场景 B），需要强制转为同一满布局，后序问题则归约到第一种情况
3. 冲突和布局类型无关，仅和方向有关，可以归约到上述两种情况。
4. 由于当下象限集和目标象限集，是一个多对多的关系，所以需要一个算法保证，象限规约的合理性和稳定性。

问题域

由之前的讨论可得，这里的抽象问题域是：将一个象限集，以某种规则映射到另一个象限集。
举例说明：

定义域	值域	期望映射结果
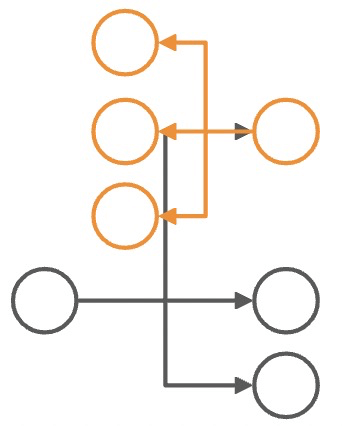象限集 [ 2 ]	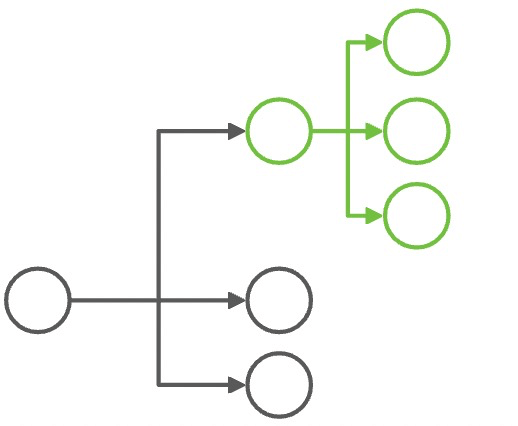象限集 [ 1 ]	2 → 1
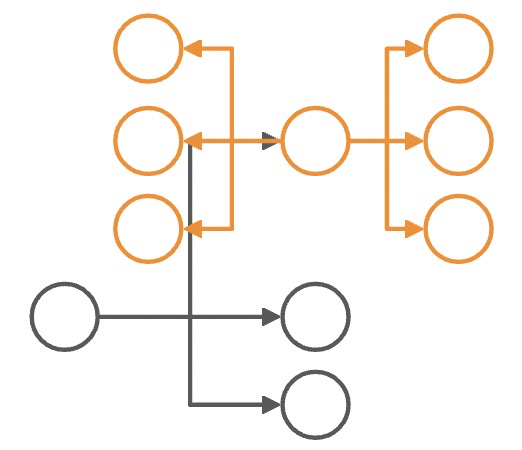象限集 [ 1, 2 ]	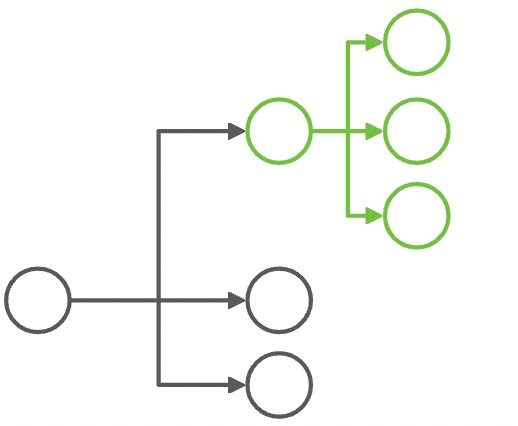象限集 [ 1 ]	1 → 1 2 → 1

根据实际产品设计，象限的归约还需要遵循就近原则，举例说明：

定义域	值域	期望映射结果
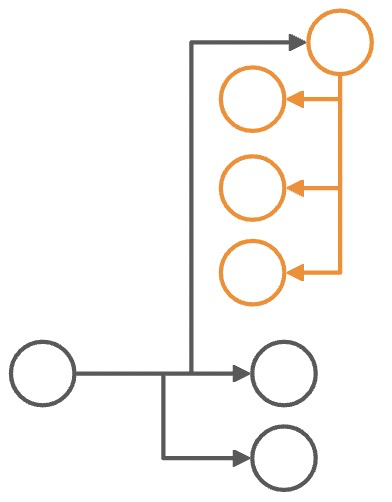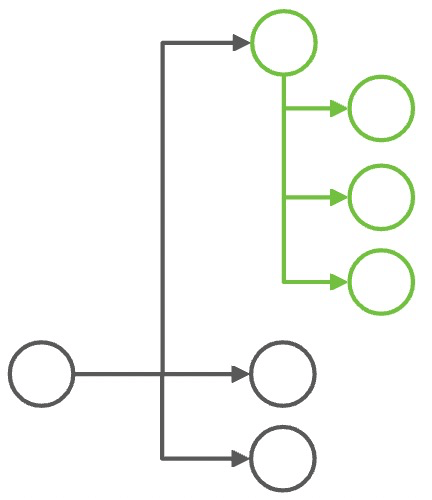[ 3 ]	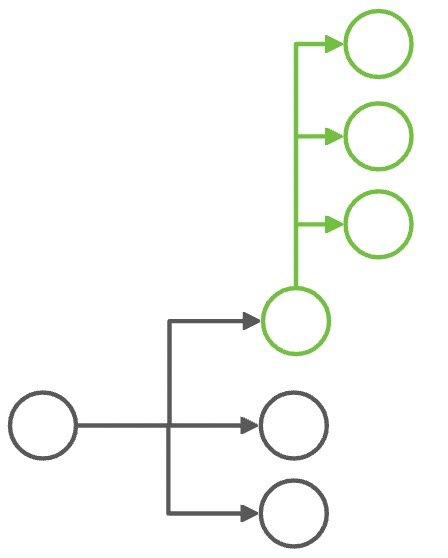[1, 4]	3 → 1

归约算法

算法比较简单，但比较关键，因为现阶段（未来可能也是），所有涉及象限归约的场景，都会落到这个算法里。核心点是：

一、确保最邻近。
二、可泛化。满足多对多的所有情况
三、周期性。确保定义域是任何值，都能映射到值域

具体流程，打个比方是：顺时针看 1 眼，逆时针看 2 眼，顺时针看 3 眼，…… 逆时针看 n+1 眼
举例说明：

当前象限	目标象限	第一步	第二步	第三步	命中结束

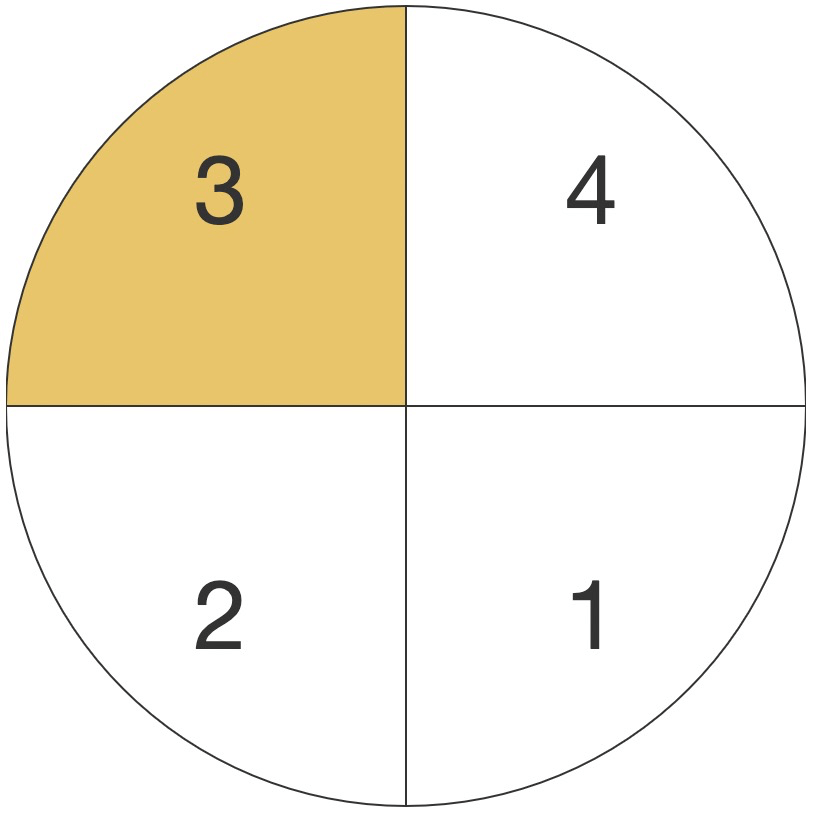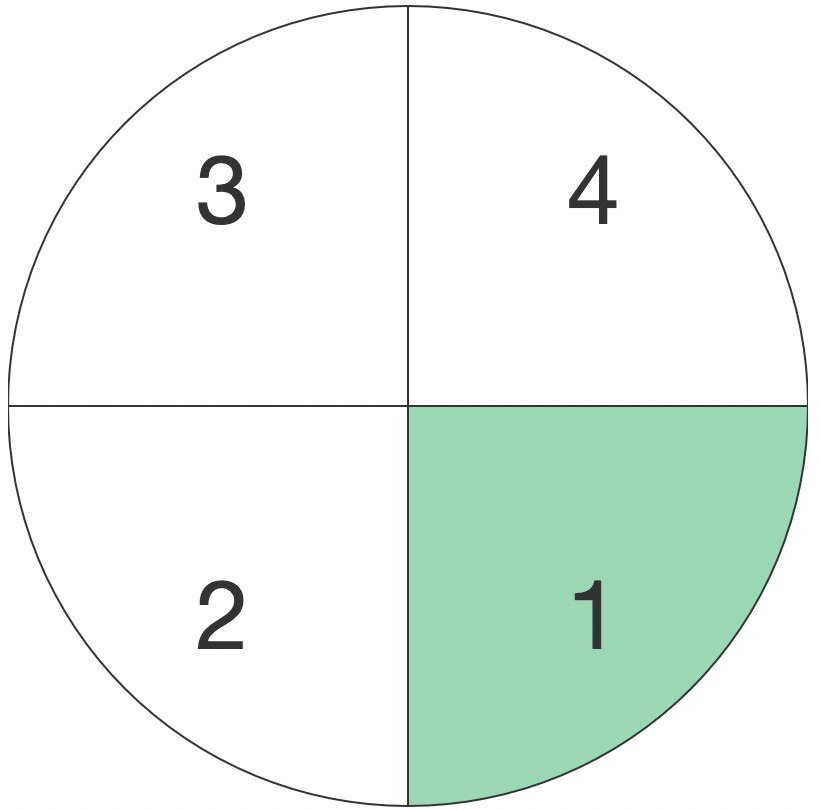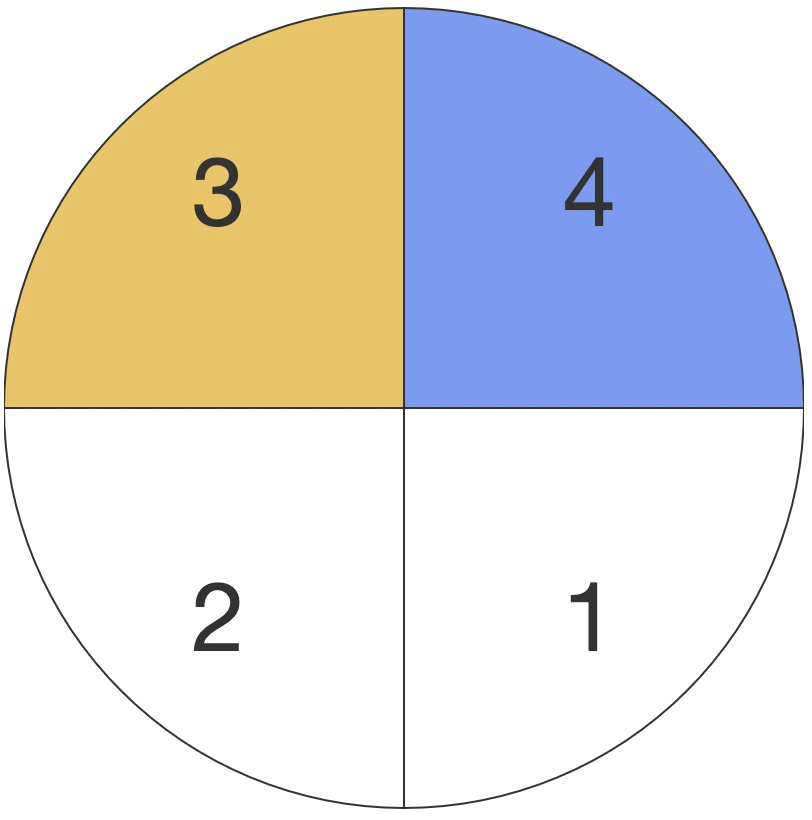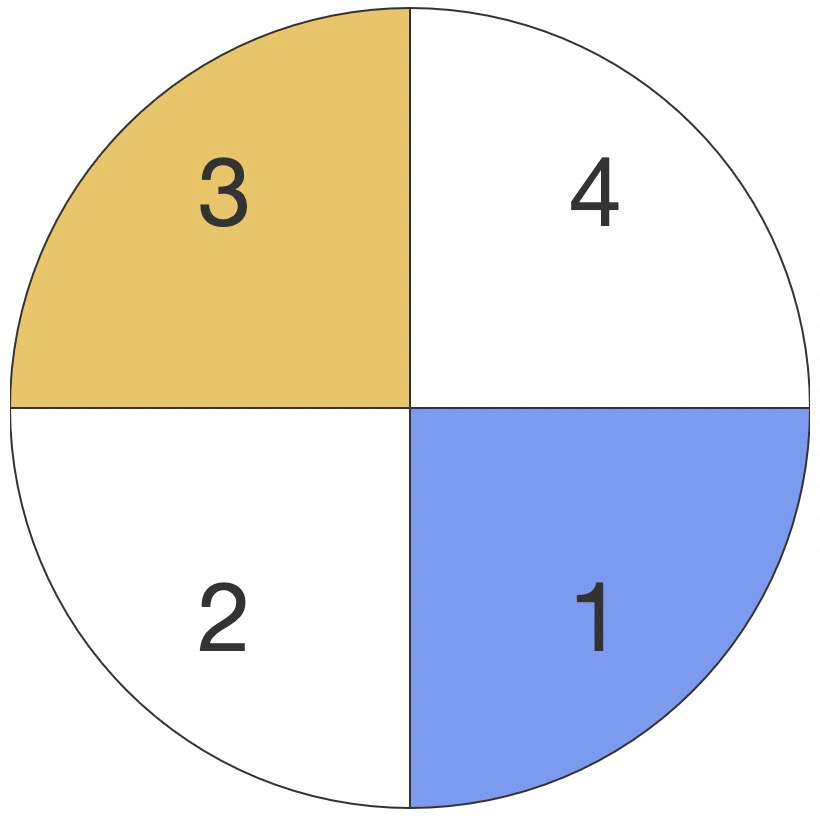具体实现，详细解释起来有点琐碎，直接上代码了，如下：

/**
 * 象限归约
 * @param {Array} domain - 当前象限定义域
 * @param {Array} range  - 目标象限值域
 * @param {Number} l     - 目标集合总长度
 */
export function quadrantReduce(domain, range, l) {
  const rst = {};
  let source, target, c;
  for (let i = 0; i < domain.length; i++) {
    source = domain[i];
    target = source;
    c = 1;
    while (!range.includes(target)) {
      if (c % 2 === 1) {
        target += c;
        if (target > l) target %= l;
      } else {
        target -= c;
        if (target < 1) target = l + target % l;
      }
      c++;
    }
    rst[source] = target;
  }
  return rst;
}

至此，我们阐释了这次子图嵌套方案的主要概念和思路。

总结

对于一张思维导图而言，结构无疑是很重要的。

这次更新从技术角度，挑战前所未有。从产品角度，也开启一扇门，一来，之前想做的一些内部场景（如：项管场景，需要标准布局嵌套鱼骨图、时间轴布局等），后续也能开始做了。二来，相信子图嵌套也能带来更大的灵活度，给用户的创作，更大的发挥空间。

最后

技术是性感的，求是求真的过程是痛苦的，更是愉悦的。希望所有技术人都能在忙碌的工作中，从技术里，在求真求是的过程里，在自己的内心中，找到最纯粹的、最本源的一份快乐。