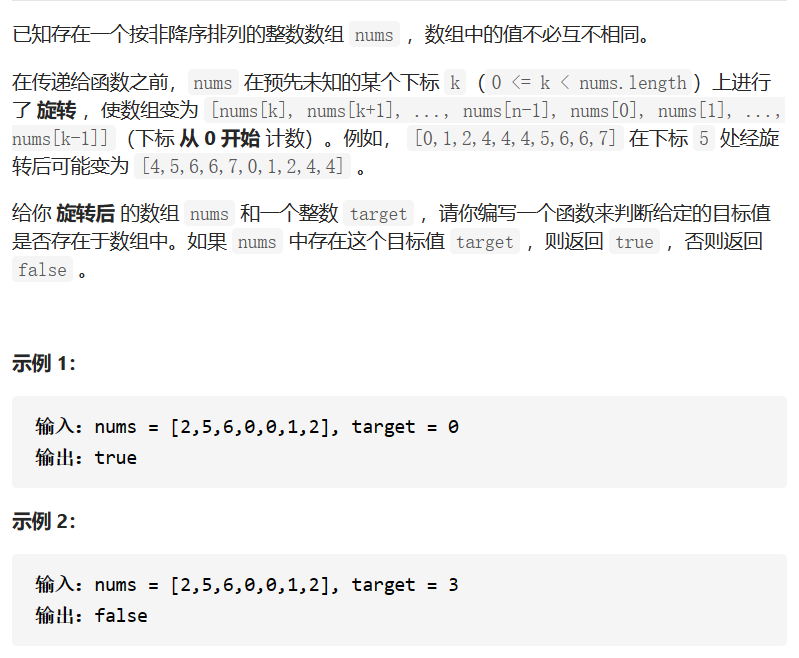
题目

解题

题目中是将一个升序数组在某一位将其数组旋转，这样就会造成两片升序搜索区
第一处：数组第一位到数组中值最大的一位（也就是数组旋转前数组最后一位）该区域数值普遍偏大，叫大数区
第二处：数组中值最小的一位（也就是数组旋转前的第一位）到 数组最后一位 该区域数值都是旋转前数组第一位到旋转位置-1 的值 相对于后面此时偏小 叫小数区
这题考察就是如何应对这个场景
我们可以将搜索区都抽象出来，我们判断target会在哪个搜索区出现，二分算法取的就是中间值，我们可以拿中间与数组最后一位比较
当 中间值 <= 数组最后一位：这个中间值在小数区，我们就可以判断target是否在小数区，如果不在，说明在左边，但是此时无法保证中间值是数组最小位，说不定左边的才是原数组第一位。将右指针移动，使其搜索左边区域，将左边区域依旧通过中间值划分成两部分，判断target在那个区域
中间 >= 数组最后一位： 这个中间值在大数区，方法大致与上面一样，
但是会有特殊情况： 如果中间值 == nums【k】,这就无法划分区域啦
代码

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {boolean}
 * 原始数组以升序排列，
 * left right target mid
 * 第一种情况： target == mid 
 * 第二种情况：left == mid 此时无法判断数组内的边界
 *            left ++ ;
 * 第三种情况: mid >= right
 *            判断target是否在 left - mid 之间
 *            在的话 将右指针移动 mid -1 不在的话 左指针右移 mid + 1
 * 第四种情况：mid <= right
 *            判断targe 是否在 mid - right 之间
 *            在的话将左指针移动 mid + 1不在的话 右指针左移 mid - 1
 * [1,1,1,1,1,1,1,1,1,1,1,1,1,2,1,1,1,1,1]
 */
var search = function(nums, target) {
    let l = 0;
    let r = nums.length - 1;
    let minIndex = 0;
    while( l <= r) {
        const mid = (l + r) >> 1;
        const curValue = nums[mid];
        if(curValue == target) return true;
        else if (curValue == nums[l]) {
            l++;
        }else if (curValue <= nums[r]){
            if(target > curValue && target <= nums[r]) {
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }else {
            if(target < curValue && target >= nums[l]) {
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        }
    }
    return false;
};