参考视频

阿里云盘： https://www.aliyundrive.com/s/gHdyew6pKNE
百度网盘：链接：https://pan.baidu.com/s/1bra63rIld3Farru0KD6aNQ
提取码：zwhf

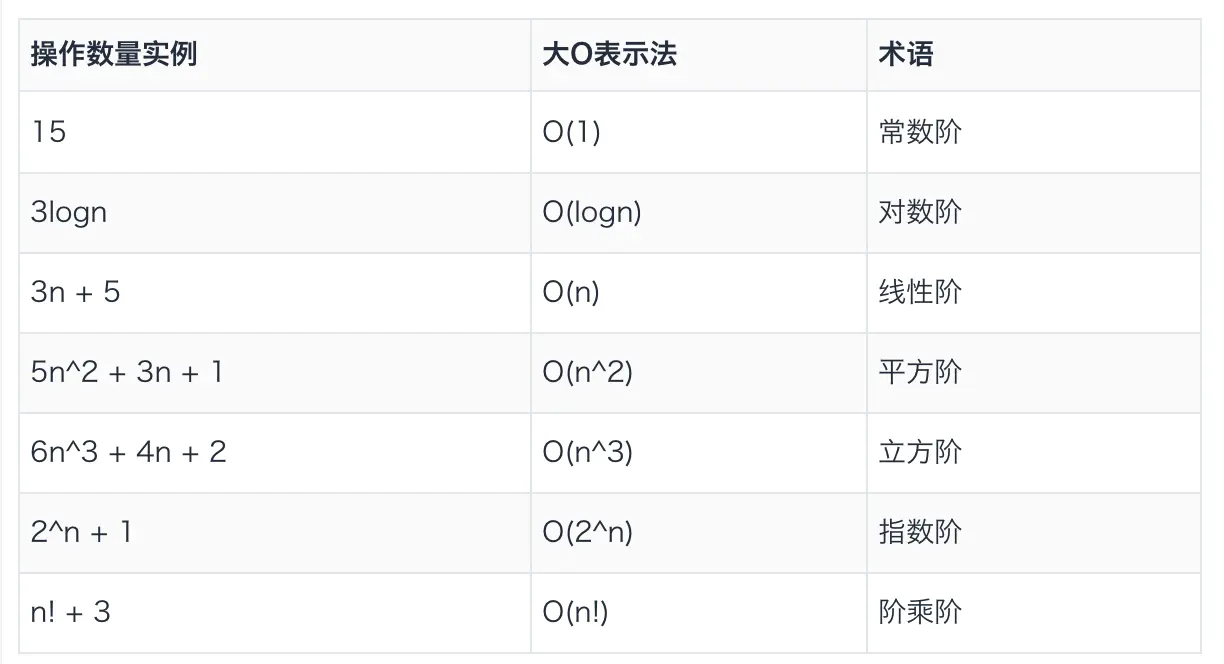
何为时间复杂度

时间复杂度，由于算法程序无法具体计算程序所消耗的时间，而将程序中的操作以阶级来划分，越是耗时越长的操作其阶级就越高，越靠下的就耗时越少，可看下面的图解。

时间复杂度分析

1.只关注循环执行次数最多的一段代码

我们在分析一段代码的时间复杂度时，我们只要关注循环次数最多的那一段代码就 ok 了。 比如说在第一段代码中

  1. function total(n) { // 1
  2.       var sum = 0; // 2
  3.       for (var i = 0; i < n; i++) { // 3
  4.         sum += i; // 4
  5.       } //5 
  6.     } //6

只有第 3 行和第 4 行是执行次数最多的，分别执行了 n 次，那么忽略常数项，所以此段代码的时间复杂度就是 O(n)。

2.加法法则：总复杂度等于量级最大的那段代码的复杂度

多段代码取最大：比如一段代码中有单循环和多重循环，那么取多重循环的复杂度。
比如说，看下面这段代码的时间复杂度。

  1. function total(n) { 
  2.       // 第一个 for 循环
  3.       var sum1 = 0; 
  4.       for (var i = 0; i < n; i++) {
  5.         for (var j = 0; j < n; j++) {
  6.           sum1 = sum1 + i + j; 
  7.         }
  8.       }
  9.       // 第二个 for 循环
  10.       var sum2 = 0;
  11.       for(var i=0;i<1000;i++) {
  12.         sum2 = sum2 + i;
  13.       }
  14.       // 第三个 for 循环
  15.       var sum3 = 0;
  16.       for (var i = 0; i < n; i++) {
  17.         sum3 = sum3 + i;
  18.       }
  19.     }

我们先分别分析每段 for 循环的时间复杂度，再取他们中最大的量级来作为整段代码的时间复杂度。
第一段 for 循环的时间复杂度为 O(n)。
第二段 for 循环执行了 1000 次，是个常数量级，尽管对代码的执行时间会有影响，但是当 n 无限大的时候，就可以忽略。因为它本身对增长趋势没有影响，所以这段代码的时间复杂度可以忽略。它的时间复杂度为O(1)
第三段 for 循环的时间复杂度为 O(n)。
总上，取最大量级，所以整段代码的时间复杂度为 O(n)。

3.乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。

嵌套代码求乘积：比如递归、多重循环等。
比如说，看下面这段代码的时间复杂度

  1. function cal(n) {
  2.    let ret = 0; 
  3.    let i = 1;
  4.    for (; i < n; ++i) {
  5.      ret = ret + f(i); // 重点为  f(i)
  6.    } 
  7.  } 
  9. function f(n) {
  10.   let sum = 0;
  11.   let i = 1;
  12.   for (; i < n; ++i) {
  13.     sum = sum + i;
  14.   } 
  15.   return sum;
  16.  }

方法 cal 循环里面调用 f 方法，而 f 方法里面也有循环。
所以，整个 cal() 函数的时间复杂度就是，T(n) = T1(n) T2(n) = O(nn) = O(n) 。

4.多个规模求加法：比如方法有两个参数控制两个循环的次数，那么这时就取二者复杂度相加

  1. function cal(m, n) {
  2.   let sum_1 = 0;
  3.   let i = 1;
  4.   for (; i < m; ++i) {
  5.     sum_1 = sum_1 + i;
  6.   }
  8.   let sum_2 = 0;
  9.   let j = 1;
  10.   for (; j < n; ++j) {
  11.     sum_2 = sum_2 + j;
  12.   }
  14.   return sum_1 + sum_2;
  15. }

以上代码也是求和 ，求 sum_1 的数据规模为 m、求 sum_2 的数据规模为 n，所以时间复杂度为 O(m+n)。
公式：T1(m) + T2(n) = O(f(m) + g(n)) 。

5.多个规模求乘法：比如方法有两个参数控制两个循环的次数，那么这时就取二者复杂度相乘

  1. function cal(m, n) {
  2.   let sum_3 = 0;
  3.    let i = 1;
  4.    let j = 1;
  5.    for (; i <= m; ++i) {
  6.      j = 1; 
  7.      for (; j <= n; ++j) {
  8.        sum_3 = sum_3 +  i * j;
  9.      }
  10.    }
  11. }

以上代码也是求和，两层 for 循环 ，求 sum_3 的数据规模为 m 和 n，所以时间复杂度为 O(mn)。
**公式：T1(m) T2(n) = O(f(m) g(n)) 。*

常见的时间复杂度

只看最高量级的复杂度，下图中效率是递减的
时间复杂度 - 图1

时间复杂度图例

如上图可以粗略的分为两类，多项式量级和非多项式量级。其中，非多项式量级只有两个：O(2) 和 O(n!) 对应的增长率如下图所示
图1：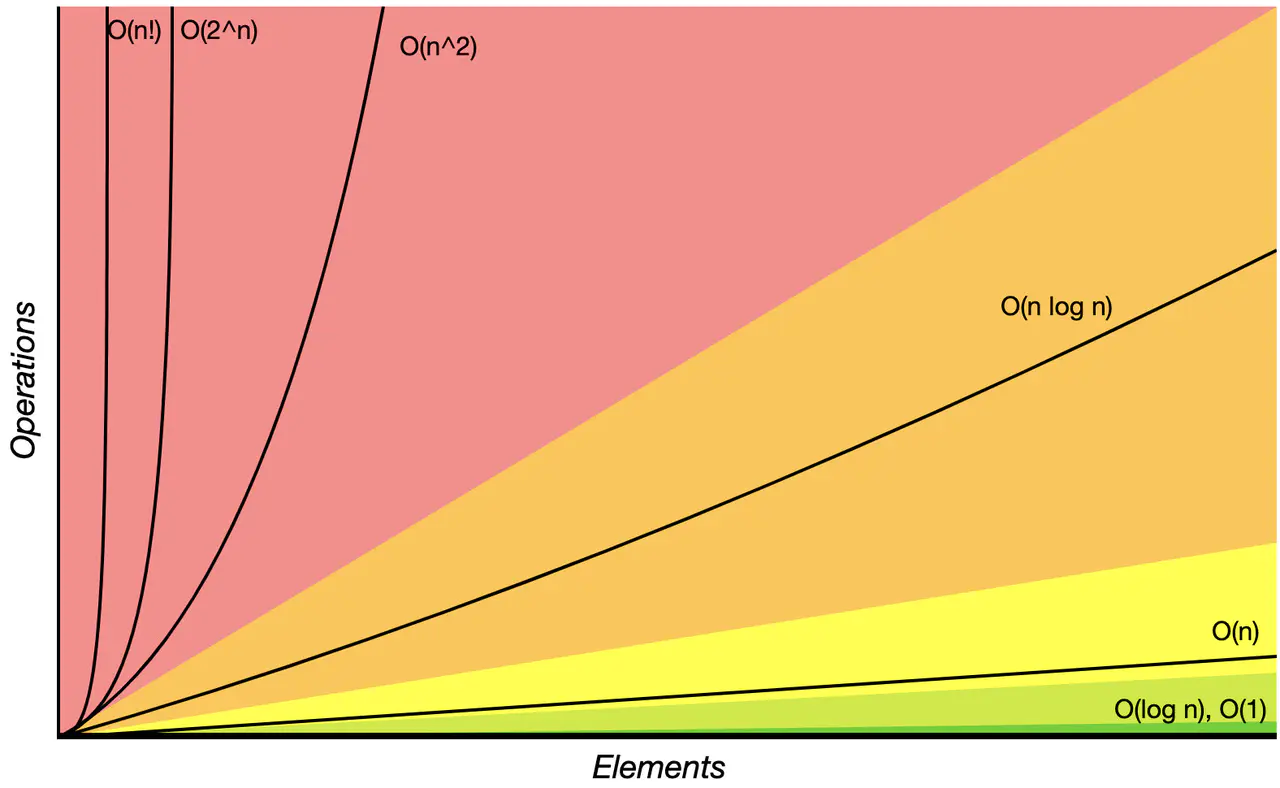
时间复杂度 - 图2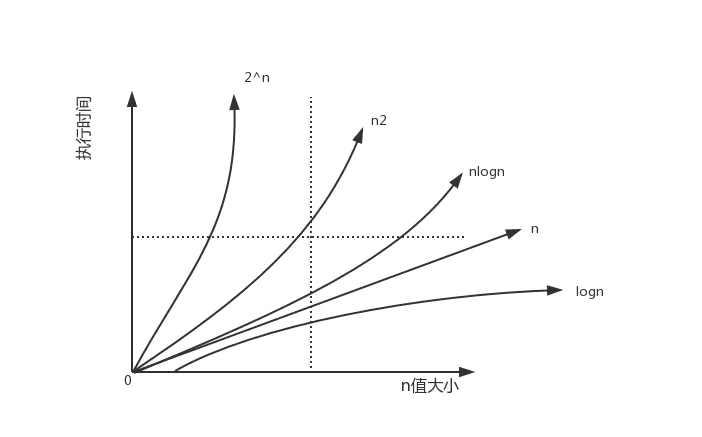
图2 ：时间复杂度 - 图3
当数据规模 n 增长时，非多项式量级的执行时间就会急剧增加，所以，非多项式量级的代码算法是非常低效的算法。

时间各个复杂度的示例

O(1)

image.png
O(1) 只是常量级时间复杂度表示法，并不是代码只有一行，比如说下面这段代码

  1. function total() {
  2.       var sum = 0;
  3.       for(var i=0;i<100;i++) {
  4.         sum += i;
  5.       }
  6.     }

虽然有这么多行，即使 for 循环执行了 100 次，但是代码的执行时间不随 n 的增大而增长，所以这样的代码复杂度就为 O(1)。
在计算复杂度的时候，O(1)一般会被忽略。但也有时间复杂度为O(1)的题

O(n)

说白就是代码需要执行n次就结束啦
for循环，while循环，(不使用二分搜索)
image.png
示例
image.png
如上图既有O(1)又有O(n），这个程序的时间复杂度为O(n)。

O(n²)

image.png
说白就是。第一个for循环执行啦n次第一个for循环中嵌套的for循环就执行n*n也就是n²次，那吗这段代码的时间复杂度就是O(n²)

区分特殊情况下的O(n)与O(n²)

仔细想想程序执行啦多少次
for循环并列
image.png
for循环是O(n) 但是有两个for循环但没有并列如上图那种，就是O(n)+O(n) 也即是O(2n) 但是没有这种概念的，称之为O(n)

循环嵌套，但是嵌套的循环并不是两个独立的，而是交替运算的，就像是两个for循环嵌套完成啦一个for循环的事
image.png
上图中第一个while循环执行n次时间复杂度为O(n)其中嵌套的while循环的时间复杂度为O(n²)但是你看整体代码的你会发现两个while循环干的却是一个while循环的事
这样的代码就可以被优化啦
代码如下

  1. while(i < n) {
  2.   i += 2;
  3. }

这样一想的话时间复杂度为O(n)

O(logn)、O(nlogn)

O(logn)

对数阶时间复杂度的常见代码如下

  1.  function total1(n) {
  2.       var sum = 0;
  3.       var i = 1;
  4.       while (i <= n) {
  5.         sum += i;
  6.         i = i * 2;
  7.       }
  8.     }
  9.     function total2(n) {
  10.       var sum = 0;
  11.       for (var i = 1; i <= n; i = i * 2) {
  12.         sum += i;
  13.       }
  14.     }

上面两个函数都有一个相同点，变量 i 从 1 开始取值，每循环一次乘以 2，当大于 n 时，循环结束。实际上，i 的取值就是一个等比数列，就像下面这样

2 2 2 … 2… 2 =n;

所以只要知道 x 的值，就可以知道这两个函数的执行次数了。那由 2 = n 可以得出 x = logn，所以这两个函数的时间复杂度为 O(logn)。
再看下面两个函数的时间复杂度

  1.  function total1(n) {
  2.       var sum = 0;
  3.       var i = 1;
  4.       while (i <= n) {
  5.         sum += i;
  6.         i = i * 3;
  7.       }
  8.     }
  9.     function total2(n) {
  10.       var sum = 0;
  11.       for (var i = 1; i <= n; i = i * 3) {
  12.         sum += i;
  13.       }
  14.     }

由上可以得知，这两个函数的时间复杂度为 O(logn) 。
由于我们可以忽略常数，也可以忽略对数中的底数，所以在对数阶复杂度中，统一表示为 O(logn)；那 O(nlogn) 的含义就很明确了，时间复杂度 为O(logn) 的代码执行了 n 次。

下面举例说明 O(nlogn)

  1. function aFun(n){
  2.   let i = 1;
  3.   while (i <= n)  {
  4.      i = i * 2;
  5.   }
  6.   return i
  7. }
  9. function cal(n) { 
  10.    let sum = 0;
  11.    for (let i = 1; i <= n; ++i) {
  12.      sum = sum + aFun(n);
  13.    }
  14.    return sum;
  15.  }

aFun 的时间复杂度为 O(logn)，而 cal 的时间复杂度为 O(n)，所以上面代码的时间复杂度为 T(n) = T1(logn) T2(n) = O(lognn) = O(nlogn) 。

O(m+n)、O(m*n)

再来看一段特殊的代码时间复杂度，比如说

  1.  function total(m,n) {
  2.       var sum1 = 0;
  3.       for (var i = 0; i < n; i++) {
  4.         sum1 += i;
  5.       }
  6.       var sum2 = 0;
  7.       for (var i = 0; i < m; i++) {
  8.         sum2 += i;
  9.       }
  10.       return sum1 + sum2;
  11.     }

因为我们无法评估 m 和 n 谁的量级比较大，所以就不能忽略掉其中一个，这个函数的复杂度是有两个数据的量级来决定的，所以此函数的时间复杂度为 O(m+n)；那么 O(m*n) 的时间复杂度类似。

非多项式阶：随着数据规模的增长，算法的执行时间和空间占用暴增，这类算法性能极差。

包括 O(2)（指数阶）、O(n!)（阶乘阶）。
O(2)（指数阶）例子：

  1. aFunc( n ) {
  2.     if (n <= 1) {
  3.         return 1;
  4.     } else {
  5.         return aFunc(n - 1) + aFunc(n - 2);
  6.     }
  7. }

参考答案： 显然运行次数，T(0) = T(1) = 1，同时 T(n) = T(n - 1) + T(n - 2) + 1，这里的 1 是其中的加法算一次执行。 显然 T(n) = T(n - 1) + T(n - 2) 是一个斐波那契数列，通过归纳证明法可以证明，当 n >= 1 时 T(n) < (5/3)，同时当 n > 4 时 T(n) >= (3/2)。 所以该方法的时间复杂度可以表示为 O((5/3))，简化后为 O(2)。 可见这个方法所需的运行时间是以指数的速度增长的。 如果大家感兴趣，可以试下分别用 1，10，100 的输入大小来测试下算法的运行时间，相信大家会感受到时间复杂度的无穷魅力。

如何确定时间复杂度

算法程序整体的复杂度是以程序中复杂度最高的为准。
算法程序的复杂度越高越说明该算法程序能被优化，注意此处可能会忽略空间复杂度
复杂度永远看最高的。