题目

给你一个长度为 n 的整数数组，请你判断在 最多 改变 1 个元素的情况下，该数组能否变成一个非递减数列。

我们是这样定义一个非递减数列的： 对于数组中任意的 i (0 <= i <= n-2)，总满足 nums[i] <= nums[i + 1]

实例

实例1：

  1. 输入: nums = [4,2,3]
  2. 输出: true
  3. 解释: 你可以通过把第一个4变成1来使得它成为一个非递减数列。

实例2：

  1. 输入: nums = [4,2,1]
  2. 输出: false
  3. 解释: 你不能在只改变一个元素的情况下将其变为非递减数列。

题解

刚开始我还以为就是单纯的判断是否为递增数列，就没多想。当提交没通过时我有点意外， 【3,4,2,3】，让我很迷惑这题在考察啥？让我迷惑不已。
而这道题考察的是低谷问题，而且解题思路也很简单，你可以抽象为你在马路上走，但是马路上有坑，你见坑填坑不就好啦吗。把坑填啦不就是一条平坦马路啦吗。但是要填几次这就不知道啦。

低谷填坑示例

对于数组构造峰谷折线图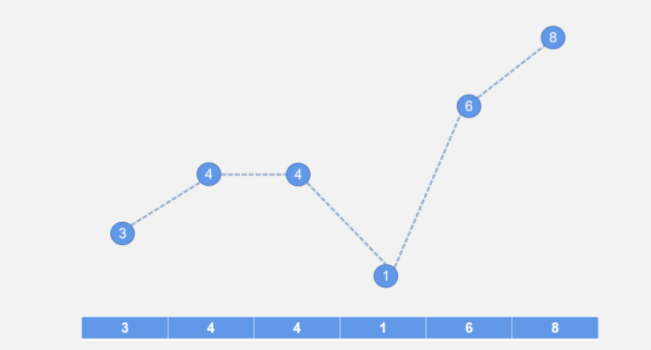
image.png
4 1 6 形成低谷，其中 1 为谷底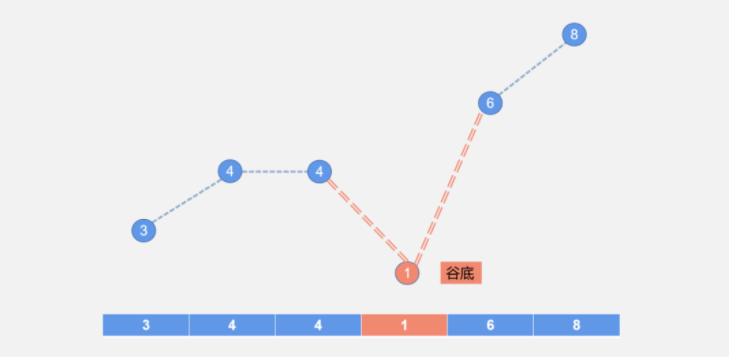
image.png
两端谷峰分别为 4， 6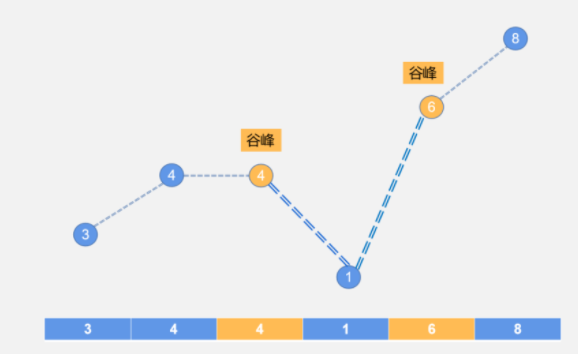
image.png
填平谷底可选取值范围，两端峰值内闭合区域，为了方便，选取两端峰值作为可选填坑值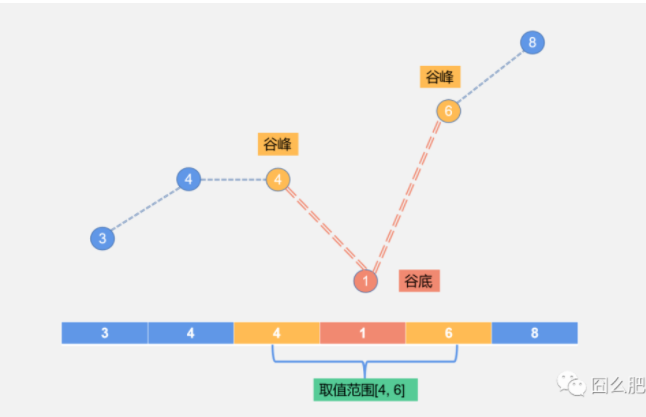
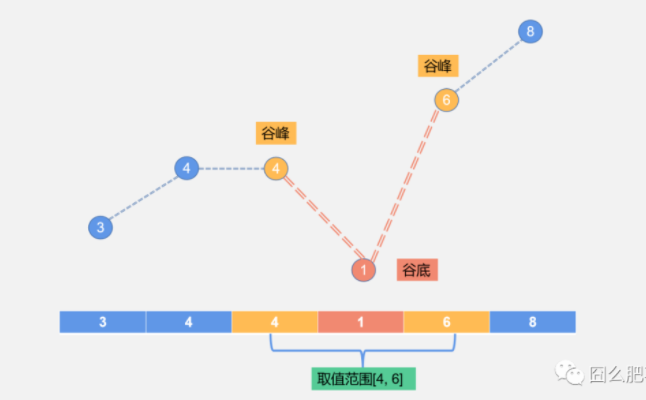image.png
image.png选取左端峰值作为填坑值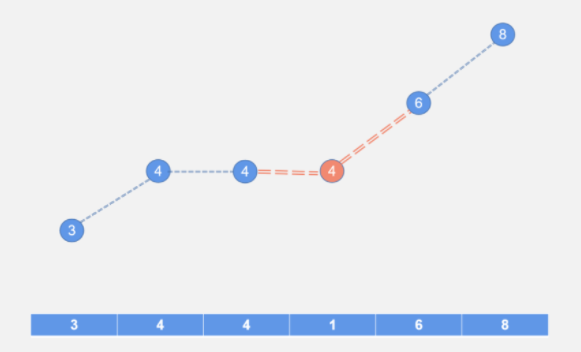
image.png
选取右端峰值作为填坑值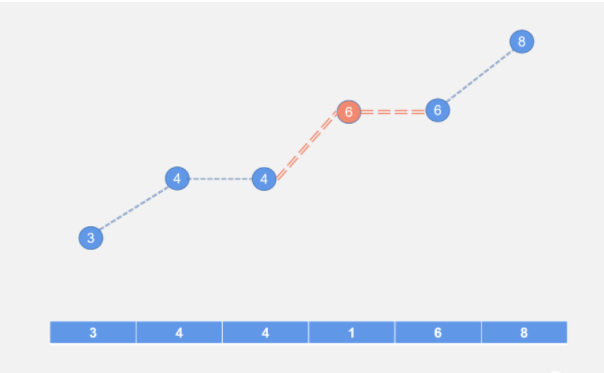
image.png
那它是选取左端峰值还是右端峰值呢？

选取峰值

1：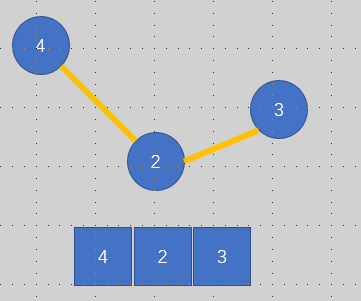
image.png
你看这种情况，是不是将峰变成谷 将4 变成2
2：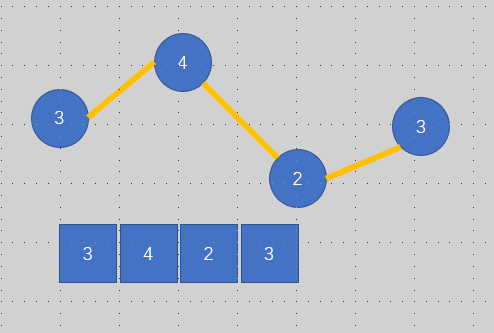
image.png
这种情况谷选哪个峰值，不确定的你看下面这张图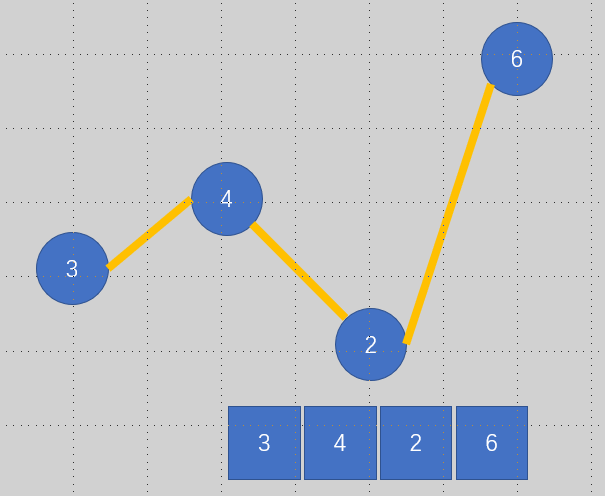
image.png
这样图毫无疑问的两端都可选，都可以选的前提条件是啥，右峰比左峰高，想上面那种右峰比左峰低那就得选左锋啦
3：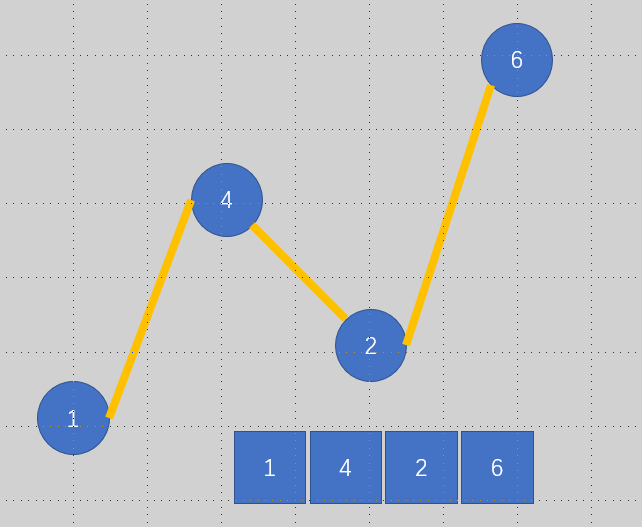
image.png
这个图1是谷 2也是谷 4是峰 我们可以将峰变成谷 也就是变成2 变成 【1 2 2 6】和【1 1 2 6】

总结这三张图的规律

1：开局是峰，峰成谷
2：谷峰谷谷， 选左峰
3：谷峰谷峰： 峰边谷
你会发现峰变成谷的情况为 开局就是峰，要吗谷峰谷峰且第二谷大与第一个谷也就是例子3中 2 > 1 但这种可以有两个选择，我们结合第一种峰变谷 峰变成右谷也就是【1 2 2 6】
那吗其余情况就是选左峰

代码实现

  1. /**
  2.  * @param {number[]} nums
  3.  * @return {boolean}
  4.  * 4 2 3
  5.  * 3,4,2,3
  6.  * 7 1 2 3 5
  7.  * -1 4 2 3
  8.  * 4 2 1
  9.  */
  10. var checkPossibility = function (nums) {
  11.   let total = 1;
  12.   for (let i = 1; i <= nums.length - 1; i++) {
  13.     const nowNumsItem = nums[i];
  14.     const prevNumsItem = nums[i - 1];
  15.     if (nowNumsItem < prevNumsItem) {
  16.       total--;
  17.       if (total < 0) return false;
  18.       if (i == 1 || nowNumsItem >= nums[i - 2]) {
  19.         nums[i - 1] = nowNumsItem;
  20.       } else {
  21.         nums[i] = prevNumsItem;
  22.       }
  23.     }
  24.   }
  25.   return total >= 0;
  26. };