普里姆算法 //加点法

如上图

普利姆算法（加点法）

1：任选一个点作为起点
2：找到以当前选中点为起点路径最短的边
3：如果这个边的另一端没有被连通进来，那就连接
4：如果这个边的另一端也早就连进来，则看倒数第二短的边
5：重复2-4的步骤直到将所有的点都连通为止
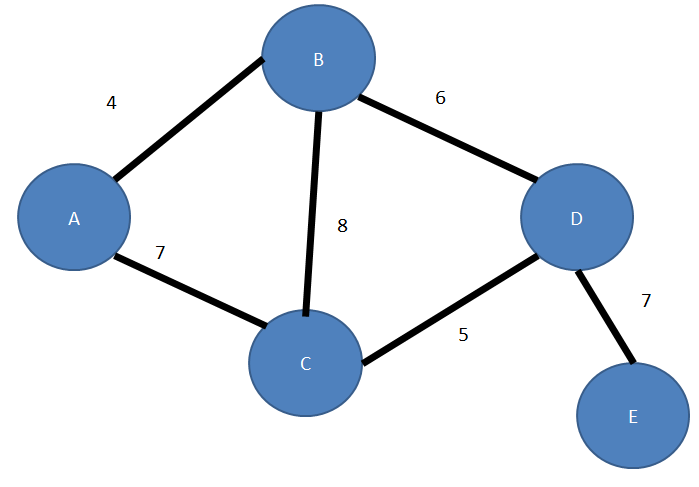
当起始点为C时连接步骤为
C->D->B->A->E
用代码实现为
其上图中路线的图的关系为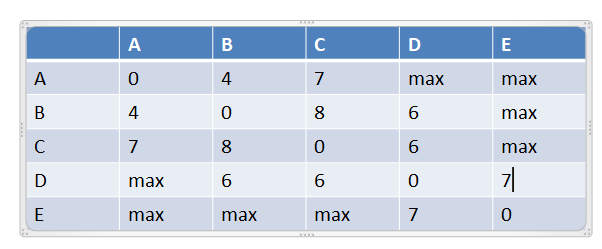

就可以是用二维数组表示图的关系

let max = 999999;
let pointSet = []; //储存点
let distance = [
    [0, 4, 7, max, max],
    [4, 0, 8, 6, max],
    [7, 8, 0, 5, max],
    [max, 6, 5, 0, 7],
    [max, max, max, 7, 0]
] // 将图的信息储存下来
class Node {
    constructor(value) {
        this.value = value;
        this.neighbor = [];
    }
}
let a = new Node('A');
let b = new Node('B');
let c = new Node('C');
let d = new Node('D');
let e = new Node('E');
pointSet.push(a)
pointSet.push(b)
pointSet.push(c)
pointSet.push(d)
pointSet.push(e)
/**
 *获取点的索引
 * @param {*} str  点
 * @returns 返回点的索引值
 */
function getIndex(str) {
    for (let i = 0; i < pointSet.length; i++) {
        if (pointSet[i].value == str) {
            return i;
        }
    }
    return -1;
}
/**
 * 获取距离最短的点
 * @param {*} pointSet  点的集合
 * @param {*} distance  线的集合
 * @param {*} nowPointSet  已连接点的集合
 */
function getMinDisNode(pointSet, distance, nowPointSet) {
    let min = max; // 最大值
    let startNode = null; //开始节点
    let endNode = null; // 结束节点
    for (let i = 0; i < nowPointSet.length; i++) {
        let index = getIndex(nowPointSet[i].value)
        for (let j = 0; j < distance[index].length; j++) {
            let thisNode = pointSet[j]
            let thisValue = distance[index][j]
            //满足不能有重复点，且距离最短
            if (nowPointSet.indexOf(thisNode) < 0 && thisValue < min) {
                min = thisValue;
                startNode = nowPointSet[i];
                endNode = thisNode;
            }
        }
    }
    startNode.neighbor.push(endNode)
    endNode.neighbor.push(startNode)
    return endNode
}
function prim(pointSet, distance, start) {
    let nowPointSet = [];
    nowPointSet.push(start);
    while (true) {
        let endNode = getMinDisNode(pointSet, distance, nowPointSet)
        nowPointSet.push(endNode)
        if (nowPointSet.length == pointSet.length) {
            break;
        }
    }
}
prim(pointSet, distance, pointSet[2])
console.log(pointSet)