青蛙跳台阶

一个青蛙，一次只能跳一级台阶，或者跳两级台阶。

问这个青蛙跳上n级台阶有多少种跳法

解析

当青蛙处于第n阶台阶，那吗青蛙就是从 (n-1) 或者从(n-2)的台阶上跳上去的。
那吗(n-1)就是从(n-1-1)处或者从(n-1-2)处跳上来的，这种结构不就是二叉树吗
以青蛙跳上第4级台阶为例会有多少种跳法
解析
当前台阶为第四级台阶
那吗青蛙就是从第3级台阶或者从第2级台阶跳上来的
第一种情况
那吗第3级台阶有可能是从第2级台阶或者第1级台阶跳上来的
那吗第2级台阶是从第1级台阶跳上来的，第二种是第0级台阶这样无意义
第二种情况
那吗第二级台阶是从第一级台阶跳上来的，第二种是第0级台阶这样无意义
用二叉树显示为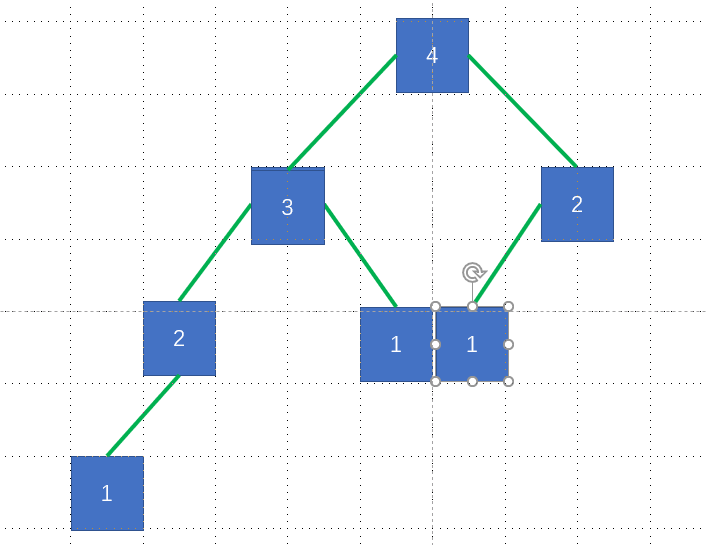

从上图查看有几种情况
从左子树（也就是节点3）开始
第一种情况：1,1,1,1

第一种情况：2,1,1
第三种情况：1,2,1
再从右子树开始（也就是节点2）
第四种情况： 1,1,2
第五种情况：2,2
正确答案就是五种，所以跳上第n级节点的跳法就是左子树的深度加上右子树的深度
公式为 jump(n) = jump(n - 1) + jump(n - 2)

利用代码实现

function jump(n) {
    if ( n <= 0 ) return -1;
    if ( n == 1 ) return 1;
    if ( n == 2 ) return 2;
    return jump(n - 1) + jump(n - 2 );
}
console.log(jump(4))