🚩传送门：牛客题目

题目

已知[NC]86. 矩阵元素查找 - 图1一个有序矩阵[NC]86. 矩阵元素查找 - 图2，同时给定矩阵的大小 [NC]86. 矩阵元素查找 - 图3 和 [NC]86. 矩阵元素查找 - 图4 以及需要查找的元素[NC]86. 矩阵元素查找 - 图5，且矩阵的行和列都是从小到大有序的。

设计查找算法返回所查找元素的二元数组，代表该元素的行号和列号（均从零开始）。保证元素互异。

解题思路：贪心

该矩阵的每行、每列都是从小到大递增的. 根据这个条件, 我们可以从左下开始找, 然后这样判断：

当从左下角开始的时候我们只有两个方向，要么向上，要么向右

  • 当向右的时候代表包括当前所在列的左边部分全部被舍弃
  • 当向上的时候代表包括当前所在行的下边部分全部被舍弃
  1. 如果当前值大于目标值：那么根据该矩阵的特性, 其右边的数只可能更大，我们往上走一步。
  2. 如果当前值小于目标值：那么上边的数只可能更小，我们往右走 。

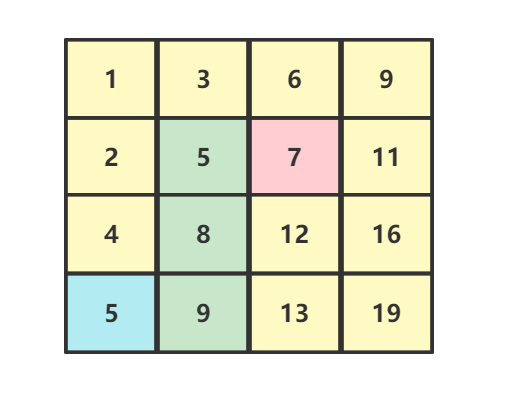
image.png
例如：我们从左下角 [NC]86. 矩阵元素查找 - 图7 开始，目标值为[NC]86. 矩阵元素查找 - 图8 。

  1. [NC]86. 矩阵元素查找 - 图9 , 说明[NC]86. 矩阵元素查找 - 图10 上边的一定都比[NC]86. 矩阵元素查找 - 图11 小，所以向右走
  2. [NC]86. 矩阵元素查找 - 图12 ，说明 [NC]86. 矩阵元素查找 - 图13右边的一定都比[NC]86. 矩阵元素查找 - 图14 大，所以向上走
  3. [NC]86. 矩阵元素查找 - 图15 ，说明 [NC]86. 矩阵元素查找 - 图16右边的一定都比[NC]86. 矩阵元素查找 - 图17 大，所以向上走
  4. [NC]86. 矩阵元素查找 - 图18 , 说明 [NC]86. 矩阵元素查找 - 图19上边的一定都比[NC]86. 矩阵元素查找 - 图20 小，所以_向右**走
  5. [NC]86. 矩阵元素查找 - 图21 ， 找到答案

复杂度分析

时间复杂度：[NC]86. 矩阵元素查找 - 图22，其中 [NC]86. 矩阵元素查找 - 图23 为数组的行数， [NC]86. 矩阵元素查找 - 图24 为数组的列数。

空间复杂度：[NC]86. 矩阵元素查找 - 图25，使用常数的空间

我的代码

  1. public int[] findElement(int[][] mat, int n, int m, int x) {
  2.     int i=n-1,j=0;
  3.     while(mat[i][j]!=x){
  4.         if(mat[i][j]<x){
  5.             j++;
  6.         }else if(mat[i][j]>x){
  7.             i--;
  8.         }else break;
  9.     }
  10.     return new int[]{i,j};
  11. }