[NC]245. 杨辉三角

🚩传送门：牛客题目
力扣题目

题目

给定一个非负整数 numRows，生成杨辉三角的前 numRows行。

注意：在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 5 输出: [
[1], [1,1],
[1,2,1], [1,3,3,1], [1,4,6,4,1] ]

解题思路：取巧解法

观察后不难发现规律，某行元素等于上一行元素往后错一位再逐个相加。

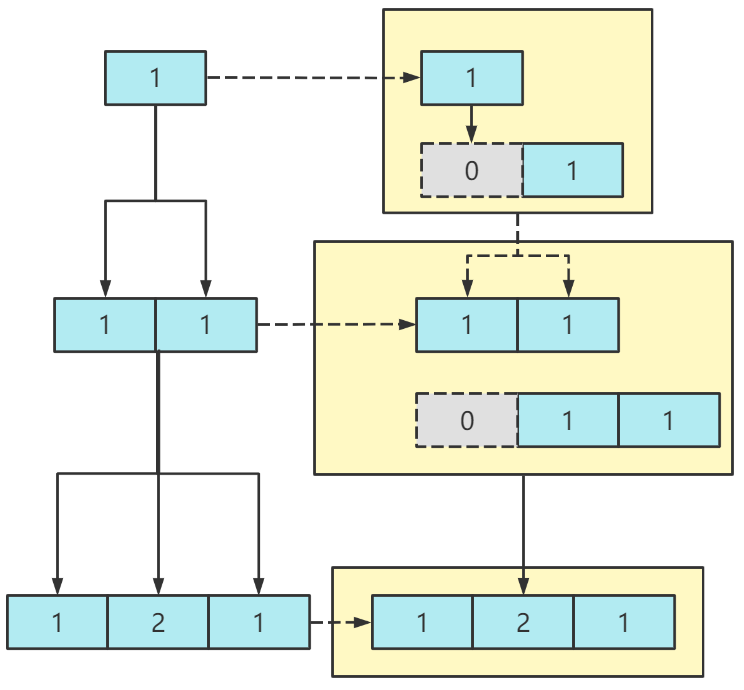
解题思路：数学

每个数字等于上一行的左右两个数字之和，可用此性质写出整个杨辉三角。即第 行的第 个数等于第 行的第 个数和第 个数之和。

但二者本质上还是肩部元素相加

复杂度分析

时间复杂度：，其中 为行数 。

空间复杂度：，不考虑返回值的空间占用。

官方代码

public class Solution {
    public int[][] generate (int num) {
        int[][] arr = new int[num][];
        for(int i = 0; i < num; i++) {
            arr[i] = new int[i+1];
            for(int j = 0; j <= i; j++) {
                // 首尾为1
                if(j == 0 || j == i) {
                    arr[i][j] = 1;
                } else {
                    // 肩部相加
                    arr[i][j] = arr[i-1][j] + arr[i-1][j-1];
                }
            }
        }
        return arr;
    }
}