🚩[LeetCode]dp304 二维区域和检索-矩阵不可变

传送门：https://leetcode-cn.com/problems/range-sum-query-2d-immutable/

题目

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

                                            ![](https://cdn.nlark.com/yuque/0/2021/png/2955945/1618387760782-453d462a-9c96-46ea-bf09-4d8c2106b7fb.png#align=left&display=inline&height=287&margin=%5Bobject%20Object%5D&originHeight=573&originWidth=542&size=0&status=done&style=none&width=271)<br />上图子矩阵左上角 (row1, col1) = **(2, 1)** ，右下角(row2, col2) = **(4, 3)，**该子矩形内元素的总和为 8。

示例

给定 matrix = [ [3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5] ]

sumRegion(2, 1, 4, 3) -> 8 sumRegion(1, 1, 2, 2) -> 11 sumRegion(1, 2, 2, 4) -> 12

解题思路：一维前缀和

这道题是「303. 区域和检索 - 数组不可变」的进阶。303 题是在一维数组中做区域和检索，这题是在二维矩阵中做区域和检索。

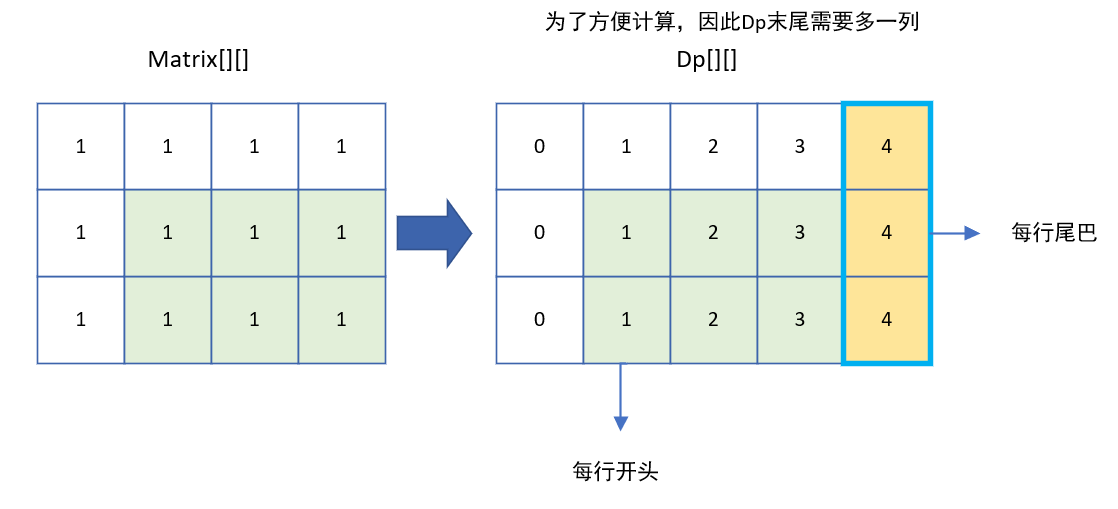
解题思路与303一致，利用前缀和求解 。 目的方便计算矩阵每行的和
设 dp[i][j] **含义：保存下标 i 行，前 j 个元素的和 。（ 故不包括 Matrix[i][j] 元素 ）

状态转移方程：

**
既得出所有的 dp[][] ，用矩阵每行的尾巴减去每行开头和，求和所有行即可。

复杂度分析

时间复杂度：

每次检索 ，其中 和 分别是矩阵 的行数和列数 。初始化需要遍历矩阵 计算二维前缀和，时间复杂度是 。
每次检索需要对二维区域中的每一行计算子数组和，二维区域的行数不超过 ，计算每一行的子数组和的时间复杂度是 ，因此每次检索的时间复杂度是 。

空间复杂度：，其中 和 分别是矩阵 的行数和列数 。
需要创建一个 行 列的前缀和数组 。

代码

我的代码

public class NumMatrix {
    int[][]dp;
    public NumMatrix(int[][] matrix) {
        dp=new int[matrix.length][matrix[0].length+1];//多一列，dp[i][j]不包括matrix[i][j]
        for (int i = 0; i < matrix.length; i++)
            for (int j = 0; j < matrix[0].length+1; j++) 
                if(j==0)dp[i][j]=0;
                else dp[i][j]=dp[i][j-1]+matrix[i][j-1];
    }
    public void sumRegion(int row1, int col1, int row2, int col2) {
        int res=0;
        for (int i = row1; i <= row2; i++) res+=dp[i][col2+1]-dp[i][col1];
        return res;
    }
    public static void main(String[] args) {
        NumMatrix matrix=new NumMatrix(new int[][]{ {3, 0, 1, 4, 2},
                                                   {5, 6, 3, 2, 1},
                                                   {1, 2, 0, 1, 5},
                                                   {4, 1, 0, 1, 7},
                                                   {1, 0, 3, 0, 5}});
        matrix.sumRegion(2, 1, 4, 3);
        matrix.sumRegion(1, 1, 2, 2);
        matrix.sumRegion(1, 2, 2, 4);
    }
}

解题思路：二维前缀和

一维前缀和虽然利用了前缀和，但是每次检索的时间复杂度是 ，仍然没有降到 。为了将每次检索的时间复杂度降到 ，需要使用二维前缀和，在初始化的时候计算二维前缀和数组。

为矩阵 以 为右下角的子矩阵的元素之和：

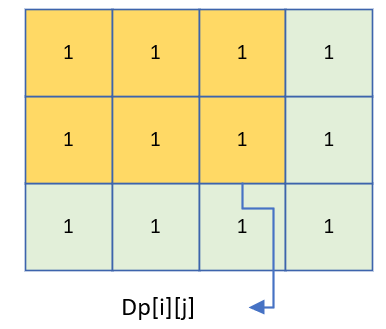
状态转移方程：

_

解释：如下图所示，状态转移的由来

当我们得到了所有的 `dp[][]` ，如**何通过 dp[][] **在** O(1) 内得到答案呢 ？
如下图所示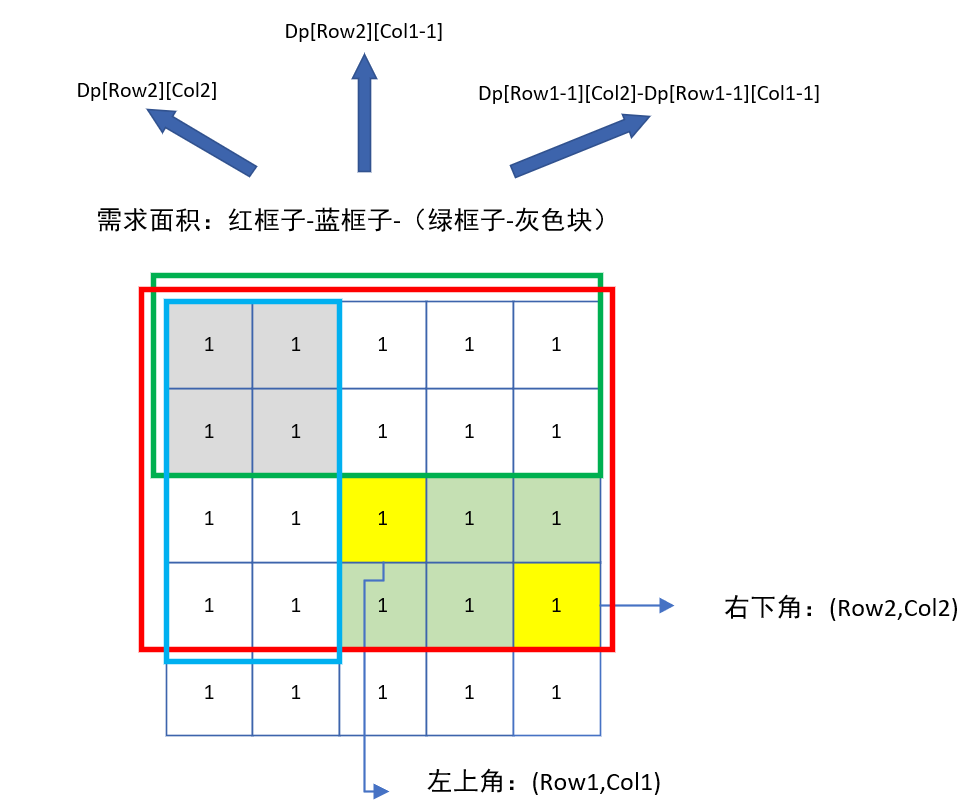

结果答案：

代码

我的代码

public class NumMatrix {
    int[][]dp;
    public NumMatrix(int[][] matrix) {
        dp=new int[matrix.length][matrix[0].length];//dp[i][j]以其做右下角的矩阵和
        for (int i = 0; i < matrix.length; i++)
            for (int j = 0; j < matrix[0].length; j++)
                if(i==0)dp[i][j]=(j>0?dp[i][j-1]+matrix[i][j]:matrix[0][0]);
                else if(j==0)dp[i][j]=dp[i-1][j]+matrix[i][j];
                else dp[i][j]=dp[i][j-1]-dp[i-1][j-1]+dp[i-1][j]+matrix[i][j];
    }
    public void sumRegion(int row1, int col1, int row2, int col2) {
        int res=0;
        if(row1==0){
            if(col1==0)return dp[row2][col2];//0行0列,起点返回值
            else return dp[row2][col2]-dp[row2][col1-1];//0行非0列,返回值
        }
        else{
            if(col1==0) return dp[row2][col2]-dp[row1-1][col2];//非0行0列,返回值
            else return dp[row2][col2]-dp[row2][col1-1]-(dp[row1-1][col2]-dp[row1-1][col1-1]);
            //非0行非0列,列返回值
        }
    }
}