解1:全排序 [ 递归形式 ]
所谓全排列,就是打印出字符串中所有字符的所有排列。例如输入字符串 abc ,则打印出 a、b、c 所能排列出来的所有字符串 abc、acb、bac、bca、cab 和 cba 。
从集合中依次选出每一个元素,作为排列的第一个元素,然后对 剩余 的元素进行 全排列 ,如此递归处理,从而得到所有元素的全排列。
以对字符串 abc 进行全排列为例,我们可以这么做:
- 固定 a,求后面 bc 的排列:abc,acb,求好后,a 和 b 交换,得到 bac
- 固定 b,求后面 ac 的排列:bac,bca,求好后,a 和 c 交换,得到 cba
- 固定 c,求后面 ba 的排列:cba,cab。
整理代码
public class Solution {public static void permutation(char[] str , int first,int end) {//输出一个排列方式if(first == end) {for(char c:str)System.out.print(c);System.out.println();}for(int i = first; i <= end ; i++) {swap(str, i, first);permutation(str, first+1, end); //固定好当前一位,继续排列后面的swap(str, i, first);}}private static void swap(char[] str, int i, int first) {char tmp;tmp = str[first];str[first] = str[i];str[i] = tmp;}public static void main(String[] args) {char[] str = {'a','b','c'};permutation(str, 0, 2); //输出str[0..2]的所有排列方式}}
解2:去重全排列
从集合中依次选出每一个元素,作为排列的第一个元素,然后对 剩余 的元素进行 全排列 ,如此递归处理,从而得到所有元素的全排列。
为了杜绝重复的全排列,我们只要 保证 作为排列的第一个元素是 不重复 的,就可以保证全排列是不重复的。
用编程的话描述就是第 i 个数与第 j 个数交换时,要求 **[i,j)** 中没有与第 j 个数相等的数。
整理代码
public class Solution {
public static void permutation(char[] str , int first,int end) {
//输出一个排列方式
if(first == end) {
for(char c:str)
System.out.print(c);
System.out.println();
}
for(int i = first; i <= end ; i++) {
# 去重关键加上能否交换的判断即可
if(can_swap(str,first,i)){
swap(str, i, first);
permutation(str, first+1, end); //固定好当前一位,继续排列后面的
swap(str, i, first);
}
}
}
private static boolean can_swap(char[] str, int i, int j) {
while(i<j){
if(str[i++]==str[j])return false;
}
return true;
}
private static void swap(char[] str, int i, int first) {
char tmp;
tmp = str[first];
str[first] = str[i];
str[i] = tmp;
}
public static void main(String[] args) {
char[] str = {'a','b','b'};
permutation(str, 0, 2); //输出str[0..2]的所有排列方式
}
}
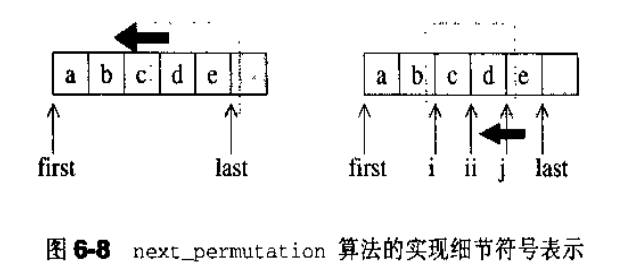
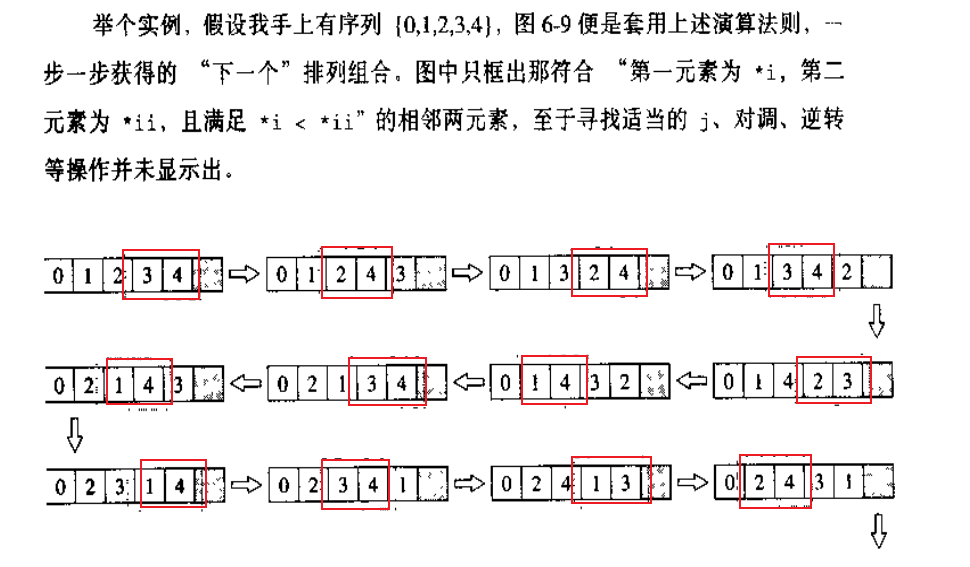
解3:next_permutation [ STL 字典全排列 ]一定不会重复
整理代码
public boolean nextPermutation(char[] arr) {
int i = arr.length - 2;
//1. 找出 i<ii 的部分
while (i >= 0 && arr[i] >= arr[i + 1]) {
i--;
}
if (i < 0) {
return false;
}
int j = arr.length - 1;
//2. 找出 j>i 的部分
while (j >= 0 && arr[i] >= arr[j]) {
j--;
}
//3. 交换(i,j)
swap(arr, i, j);
//4. 反转ii 之后元素
reverse(arr, i + 1);
return true;
}
整理代码
public class Solution {
public static boolean next_permutation(char[] str , int first,int last) {
if(first>last||first==last)return false; //只有一个元素
int i=last; //i指向尾端
while(true){
int ii=i;
//1. 找 i<ii
--i;
//以上,锁定一组(两个相邻元素)
if(str[i]<str[ii]){
int j=last+1; //令 j 指向尾端的下一个越界结点
//2. j>i
while(!(str[i]<str[--j])); //由尾端向前找,直到遇上比下标 i 大的元素
swap(str,i,j); //交换 i,j
reverse(str,ii,last); //将ii之后元素全部逆向重排
return true;
}
if(i==first){ //进行至最前面了
reverse(str,first,last); //全部逆向重排
return false;
}
}
}
private static void reverse(char[] str, int first, int last){
while(first<last){
swap(str,first,last);
first++;
last--;
}
}
private static void swap(char[] str, int i, int j) {
char tmp;
tmp = str[j];
str[j] = str[i];
str[i] = tmp;
}
public static void main(String[] args) {
//1. 非字典排序的数组
char[]str=new char[]{'c','a','b'};
//2. 将其字典排序成 a,b,c
Arrays.sort(str);
//3,如果有下一个排序序列将其输出 [全输出完就是字典全排序]
do{
for(char c:str){
System.out.print(c+" ");
}
System.out.println();
} while(next_permutation(str,0,2));
}
}
解4:prev_permutation

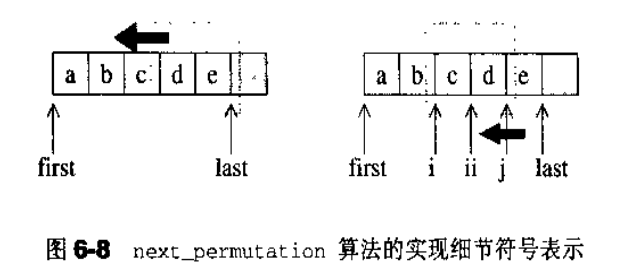
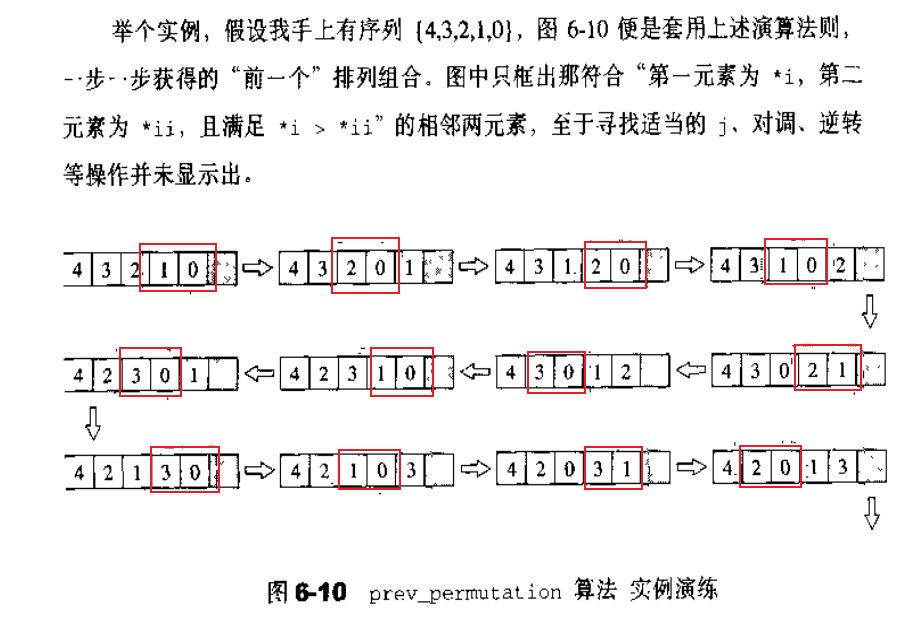
整理代码
public class Solution {
public static boolean prev_permutation(char[] str , int first,int last) {
if(first>last||first==last)return false;
int i=last;
while(true){
int ii=i;
--i;
if(str[i]>str[ii]){ //差异1:str[i]<str[ii]
int j=last+1;
while(!(str[i]>str[--j])); //差异2: while(!(str[i]<str[--j]));
swap(str,i,j);
reverse(str,ii,last);
return true;
}
if(i==first){
reverse(str,first,last);
return false;
}
}
}
private static void reverse(char[] str, int first, int last){
while(first<last){
swap(str,first,last);
first++;
last--;
}
}
private static void swap(char[] str, int i, int j) {
char tmp;
tmp = str[j];
str[j] = str[i];
str[i] = tmp;
}
public static void main(String[] args) {
//1. 非字典排序的数组
char[]str=new char[]{'c','b','a'};
//2. 如果有下一个排序序列将其输出
do{
for(char c:str){
System.out.print(c+" ");
}
System.out.println();
} while(prev_permutation(str,0,2));
}
}
解5:全组合
求全组合,则假设原有元素 个,则最终组合结果是
个
用位操作方法:假设元素原本有:a,b,c 三个,则 1 表示取该元素,0 表示不取。(3 位表示 8 种可能性)
故取 a 则是
001,取 ab 则是011
通过 **>>** 操作依次和 1 做 &运算 来判断是否包含某位的字符
例如:求解 ac
101
- 5=
**101 &1**=1 得出 包含 a- 对数字 5 做 >>1 操作,2=
**10&1**=0 得出 不包 b- 对数字 2 做 >>1 操作,1=
**1&1**=1 得出 包含 c
算法思想
- 首先遍历每一种情况
- 针对每一个情况通过 通过 `**>>**` 操作依次和 **1** 做 **&运算 **来判断每一位的字符
整理代码
public class Solution {
public static void Combination( ) {
char[] str = {'a' , 'b' ,'c'};
int n = str.length;
//1. “<<” 表示 左移:各二进位全部左移若干位,高位丢弃,低位补0。:即求1左移n位的2^n。
int nbit = 1<<n;
System.out.println("全组合结果个数为:"+nbit);
//2. 结果有nbit个。输出结果从数字小到大输出:即输出0,1,2,3,....2^n。
for(int i=0 ;i<nbit ; i++) {
System.out.print("组合数值 "+i + " 对应编码为: ");
int tmp=i;
//3. 通过 >> 操作判断是否包含第j位字符
for(int j=0; j<n ; j++) {
if((tmp & 1)!=0) {
System.out.print(str[j]);
}
tmp=tmp>>1;
if(tmp==0)break;
}
System.out.println();
}
}
public static void main(String[] args) {
Combination();
}
}