传送门：https://leetcode-cn.com/problems/maximum-product-subarray/submissions/
题目
给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。
示例 1:
输入: [2,3,-2,4] 输出: 6 解释: 子数组 [2,3] 有最大乘积 6。
示例 2:**
输入: [-2,0,-1] 输出: 0 解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
解题思路：动态规划
错误思路：
如果我们用 ![🚩[LeetCode]Dp152 乘积最大子数组 - 图1](/uploads/projects/mylearn@leetcode/5eaa3b05f644e84cc8dda42cc7b30ce7.svg)
来表示以第 ![🚩[LeetCode]Dp152 乘积最大子数组 - 图2](/uploads/projects/mylearn@leetcode/a5bc2d73d6f32f9182fe1558a2d811a2.svg)
个元素结尾的乘积最大子数组的乘积，![🚩[LeetCode]Dp152 乘积最大子数组 - 图3](/uploads/projects/mylearn@leetcode/6cfe8657146fe3d55f6a21c783416b8c.svg)
表示输入参数 ![🚩[LeetCode]Dp152 乘积最大子数组 - 图4](/uploads/projects/mylearn@leetcode/bec1ff3ae9837916a4c98a980f31f508.svg)
，那么根据「[53. 最大子序和**](https://www.yuque.com/qingxuan-u4juc/leetcode/vknvz7)」的经验，我们很容易推导出这样的状态转移方程：
![🚩[LeetCode]Dp152 乘积最大子数组 - 图5](/uploads/projects/mylearn@leetcode/971e2f8c41aadd05d262ae4b73892c53.svg)
它表示以第 个元素结尾的乘积最大子数组的乘积考虑 ![🚩[LeetCode]Dp152 乘积最大子数组 - 图7](/uploads/projects/mylearn@leetcode/e71ecadf694a6bbd351564df9246bf65.svg)
是否加入前面的 ![🚩[LeetCode]Dp152 乘积最大子数组 - 图8](/uploads/projects/mylearn@leetcode/e1807f8b65821713f72222c0cae76bcb.svg)
对应的一段，或者单独成为一段，这里两种情况下取最大值。求出所有的 之后选取最大的一个作为答案。
可是在这里，这样做是错误的。为什么呢？这里的定义并不满足「最优子结构」。
正确思路：
nums[i]是一个人玩还是跟前面人玩
其实状态转移的关键思想还是一致的，就是我当前的 是否考虑加入 ![🚩[LeetCode]Dp152 乘积最大子数组 - 图11](/uploads/projects/mylearn@leetcode/07c12222f48cc06fdad7af299bd8bbb5.svg)
，还是单独成段。
求乘法取最大值会导致每个位置要存储3种状态： [ 原因：**正正可能最大，负负可能最大，自己可能更大** ]
-  ：以当前位置  结尾的最大值-  ：以当前位置  结尾的最小值-  ：当前位置  的值
3种状态的原因：取决于 nums[i+1]
- 若 ，那么自然它希望前面的 `dp[i]` 是个最大的正数，这样 `dp[i+1]` 才可能大
- 若 ，那么自然 `dp[i+1]` 希望自己一个人玩，单独成段取 `nums[i]`
- 若 ，那么自然它希望前面的 `dp[i]` 是个最小的负数，这样 `dp[i+1]` 才可能大
状态转移方程：
**
![🚩[LeetCode]Dp152 乘积最大子数组 - 图12](/uploads/projects/mylearn@leetcode/2bf3edf08b3c0295d10a65aad4ec33a2.svg)
由于每个位置正正可能最大，负负可能最大，自己可能更大，故而三者取大，就是第 个元素结尾的乘积最大子数组的乘积。最后遍历一次dp_{max}，找出其中结尾最大的积
代码
错误代码
//算法思想是错误的
public static int maxProduct(int[] nums) {
if(nums==null||nums.length==0)return 0;
int[]dp=new int[nums.length];
int res=dp[0]=nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i]=Math.max(dp[i-1]*nums[i],nums[i]);
res=Math.max(res,dp[i]);//获取dp中的最大值
}
return res;
}
我的代码
public class Demo {
//0放dp[i]的最小值,1放dp[i]的最大值
public static int maxProduct(int[] nums) {
if(nums==null||nums.length==0)return 0;
int res=nums[0];//要返回的结果值
int[][]dp=new int[nums.length][2];
for (int i = 0; i < nums.length; i++) {
if(i==0)dp[i][0]=dp[i][1]=nums[0];
else {
dp[i][0]=Math.min(Math.min(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i]),nums[i]);
dp[i][1]=Math.max(Math.max(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i]),nums[i]);
res=Math.max(res,dp[i][1]); //结果筛选和状态转移应分离，为了效率合并处理
}
}
return res;
}
public static void main(String[] args) {
System.out.println(maxProduct(new int[]{2,3,-2,4}));
}
}
🦄大佬代码
class Demo {
public int maxProduct(int[] nums) {
// 偶数个负数，整个数组为最大值
// 奇数个负数，左边、右边取最大者
int max = Integer.MIN_VALUE;
int temp = 1;
// 从左往右, 取最大值
for(int i=0; i<nums.length; i++){
temp = temp * nums[i];
max = Math.max(max, temp);
if(nums[i]==0) temp = 1;//0不会影响max,影响Temp
}
temp = 1;
// 从右往左, 取最大值
for(int i=nums.length-1; i>=0; i--){
temp = temp * nums[i];
max = Math.max(max, temp);
if(nums[i]==0) temp = 1;
}
return max;
}
}
思路解释：
这思路其实蛮好的，偶数个负数，整个数组为最大值 [ 不一定，有可能是最大值 ]要考虑是不是有(0..1)小数，但是无关紧要，因为即使有小数也会被 max 更新。偶数个负数，整个数组为有效数组
。说明最大值会在整个数组中产生。如图，若负数有偶数个，需要用 max 刷一次整个数组 。
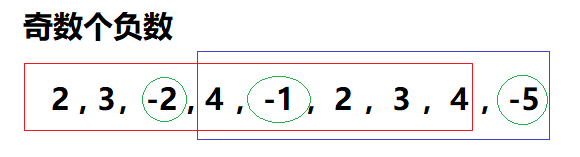
当奇数个负数时，会出现2段有效数组，如图，红色框子和蓝色框子里都是有效数组，超出一定不可能产生结果。因此需要左右遍历一次筛选最终的 max
综上所述，合并起来左右各刷一次就可以。
若有收获，就点个赞吧
0 人点赞
