[LeetCode]Dp338 比特位计数 [二进制操作]

传送门：https://leetcode-cn.com/problems/counting-bits/

题目

给定一个非负整数 num。
对于 0 ≤ i ≤ num范围中的每个数字 i ，计算其二进制数中的 1的数目并将它们作为数组返回。

示例 1:

输入: 2
输出: [0,1,1]

示例 2:

输入: 5
输出: [0,1,1,2,1,2]

一.解题思路：模拟计算->二进制优化

最直观的方法是对从0 到 num 的每个数直接计算「比特数」。

按位与运算**(&)**的一个性质是：
对于任意整数 x，令 x=x & (x−1)，该运算将 x 的二进制表示的最后一个 1 变成 0。因此，对 x 重复该操作，直到 x 变成 0，则操作次数即为 x 的「比特数」。

复杂度分析

时间复杂度：

其中 是 型的二进制位数，k=32 。需要对从 0到 num的每个数使用O(k) 的时间计算，因此时间复杂度是 O(k×num)

空间复杂度：
除了返回的数组意外，空间复杂度为常数

代码

官方代码

class Solution {
    public int[] countBits(int num) {
        int[] bits = new int[num + 1];
        for (int i = 0; i <= num; i++) {
            bits[i] = countOnes(i);
        }
        return bits;
    }
    public int countOnes(int x) {
        int ones = 0;
        while (x > 0) {
            x &= (x - 1);
            ones++;
        }
        return ones;
    }
}

二.解题思路：动态规划->最高有效位

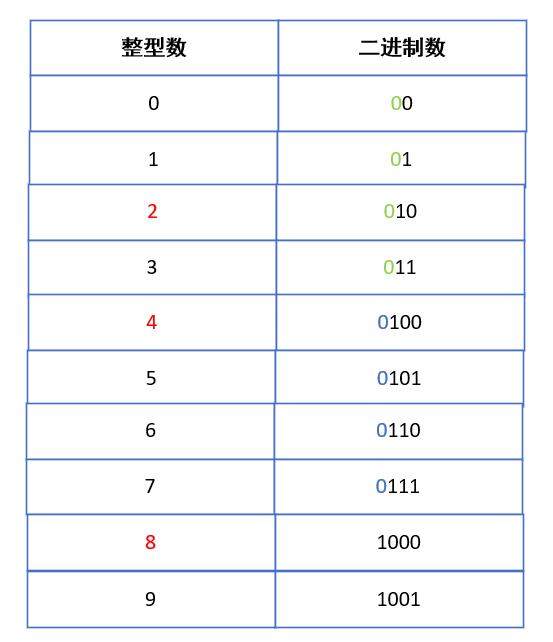
我们在观察中发现，除了 0 以外，所有数的最高位一定为 1 ，并且去除最高位后发现剩余部分其实已经统计过。
以十进制 7 为例，二进制为 111，去除最高位固定的 1 。剩余部分为 011 ，其实就是十进制的 3 ，
7-4=3 ，且 4 就是擦除的最高位 100 。整个的重点就是如何确定最高位的 100 的范围 。即最高有效位。
确定只要依靠二进制的按位与性质，若 y&(y-1)=0 则是最高有效位 。

解释最高有效位： 对于正整数 x，如果可以知道最大的正整数 y，使得 y<=x 且 y 是 2 的整数次幂，此时称 y 为 x 的「最高有效位」。则 y 的二进制表示中只有最高位是 1，其余都是 0

状态转移方程：

使用 表示当前的最高有效位，遍历从1 到 _num_ 的每个正整数 i，进行如下操作。

  - 如果 `i&(i-1)=0`，则令 `highBit=i`，更新当前的最高有效位 。
  - `i` 比 `**i-highBit**` 的二进制多一个 `1` ，因此使用状态转移方程 。 

复杂度分析

时间复杂度：

对于每个数只需要 O(1) 的时间计算 。

空间复杂度：
除了返回的数组意外，空间复杂度为常数

代码

官方代码

class Solution {
    public int[] countBits(int num) {
        int[] bits = new int[num + 1];
        int highBit = 0;
        for (int i = 1; i <= num; i++) {
            if ((i & (i - 1)) == 0) {
                highBit = i;
            }
            bits[i] = bits[i - highBit] + 1;
        }
        return bits;
    }
}

三.解题思路：动态规划->最低有效位

我们在观察中不难发现 [🦄尼玛难的丫匹]，任何一个数字都分奇偶性。
奇数的末尾一定是1，偶数的末尾一定是0
因此当去除末尾的二进制后，剩余部分的值显然先前已经计算过。因此可以实现状态转移。

对于正整数 x ,将其二进制表示右移一位，等价与将其二进制表示的最低位去掉，得到的数是 [ x/2 ]。

  - 若 `x` 是偶数，则 `bits[x]=bits[x/2]`
  - 若 `x` 是奇数，则 `bits[x]=bits[x/2]+1`

上述两种情况可以合并成：bits[x]=bits[x/2]+(x&1)

解释：当 x 为奇数 x&1 =1，奇数的末尾一定是1 当 x 为偶数 x&1 =0，偶数的末尾一定是0

以十进制偶数 6 举例子，去除末尾的 0，剩余部分是 11 也就是十进制的 3 。 6/2=3
以十进制奇数 5 举例子，去除末尾的 1，剩余部分是 10 也就是十进制的 2 。 5/2=2 [ 整型向下取整 ]

状态转移方程：

复杂度分析

时间复杂度：

对于每个数只需要 O(1) 的时间计算 。

空间复杂度：
除了返回的数组意外，空间复杂度为常数

代码

官方代码

class Solution {
    public int[] countBits(int num) {
        int[] bits = new int[num + 1];
        for (int i = 1; i <= num; i++) {
            bits[i] = bits[i >> 1] + (i & 1);
        }
        return bits;
    }
}

四.解题思路：动态规划->设置最低位

回到最初的思路上，我们解题主要依赖于二进制的按位 & 性质。

按位与运算**(&)**的一个性质是：
对于任意整数 x，令 x=x & (x−1)，该运算将 x 的二进制表示的最后一个 1 变成 0。因此，对 x 重复该操作，直到 x 变成 0，则操作次数即为 x 的「比特数」。

除了 0 以外，任意的数字最高位一定是 1 ，所以当我们执行一次按位& 操作后，其实规模已经缩小了。

状态转移方程：

复杂度分析

时间复杂度：

对于每个数只需要 O(1) 的时间计算 。

空间复杂度：
除了返回的数组意外，空间复杂度为常数

代码

官方代码

class Solution {
    public int[] countBits(int num) {
        int[] bits = new int[num + 1];
        for (int i = 1; i <= num; i++) {
            bits[i] = bits[i & (i - 1)] + 1;
        }
        return bits;
    }
}