[NC]16. 对称的二叉树

🚩传送门：牛客题目

题目

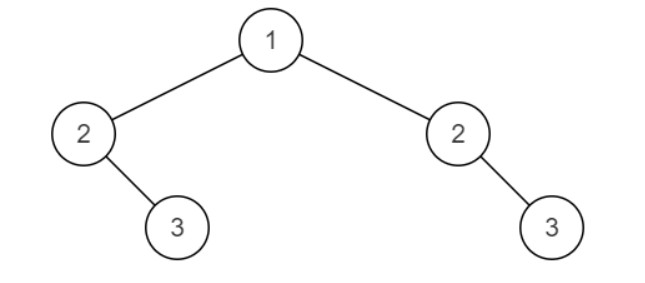
给定一棵二叉树，判断其是否是自身的镜像（即：是否对称）

例如：下面这棵二叉树是对称的

例如：下面这棵二叉树不对称。

解题思路：递归

据题意，对称二叉树定义为：「若一棵二叉树与其镜像二叉树是相同的，则其是对称的二叉树」。

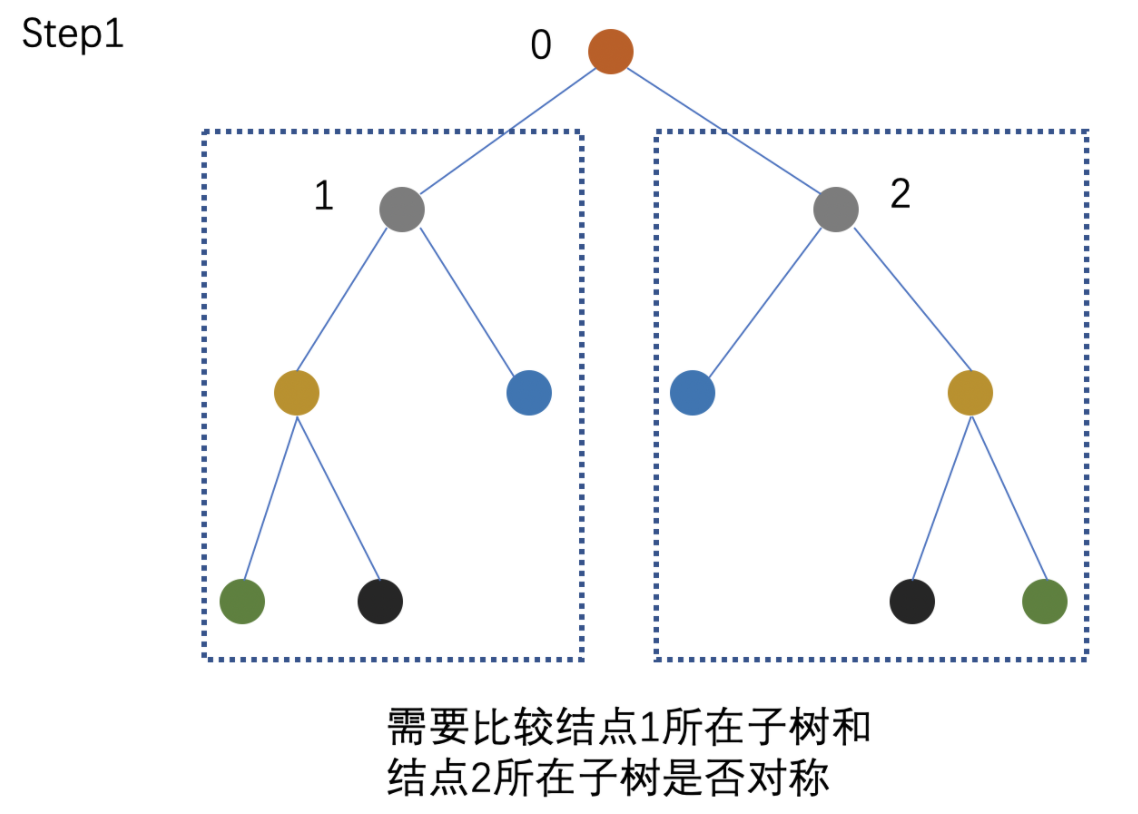
1. 从根结点开始，判断其左右子树是否对称，即判断「结点1所在子树」和「结点2所在子树」是否对称；
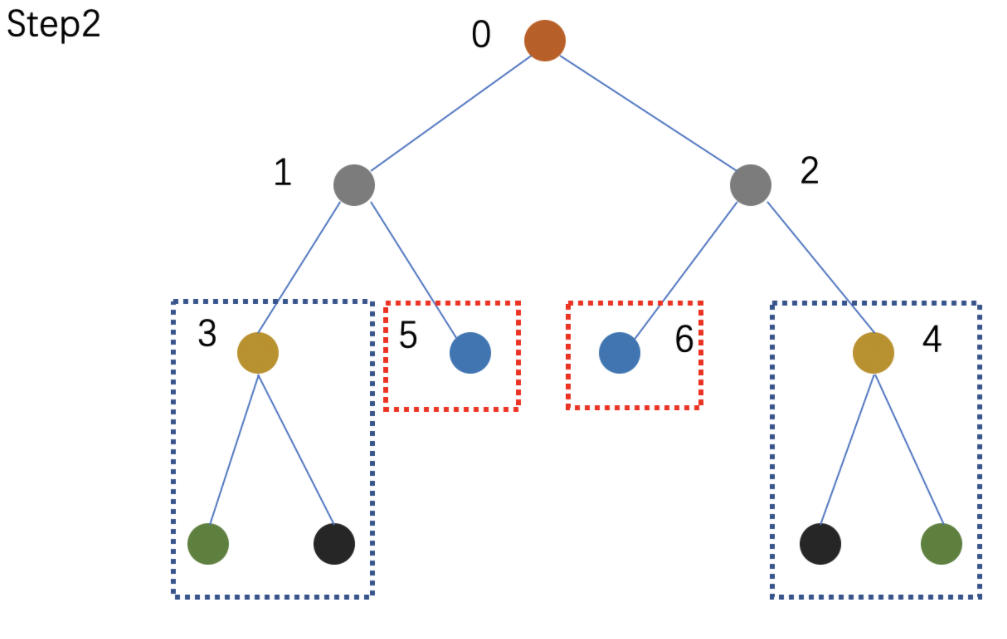
2. 为比较这两个子树的对称情况，需要分别比较各自的左右孩子的对称情况，即：比较「结点3所在子树」和「结点4所在子树」是否对称，同时也需要比较「结点5所在子树」和「结点6所在子树」是否对称；
3. 依次类推，直至遍历到叶子结点。

复杂度分析

时间复杂度： ，该方法需要遍历树的所有结点 。

空间复杂度： ，该方法在递归时需要使用栈空间 。

我的代码

class Solution {
    static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
    }
    public boolean isSymmetrical(TreeNode pRoot) {
        if (pRoot==null)
            return true;
        return helper(pRoot.left, pRoot.right);
    }
    public boolean helper(TreeNode left, TreeNode right) {
        if (left==null&&right==null) // 两个结点同时为空，必对称
            return true;
        if (left==null||right==null) // 两个结点有一个为空
            return false;
        if (left.val != right.val) // 两个结点取值不同，必不对称
            return false;
        // 递归地遍历左子树的左孩子与右子树的右孩子，以及右子树的左孩子与左子树的右孩子
        return helper(left.left, right.right) && helper(left.right, right.left);
    }
}

解题思路：非递归

利用队列进行层次遍历，将每一层用临时的列表保存下来，然后对当前一层进行判断是否对称。

由于结点数据最大 1000，所以空结点用 1001 来表示 。

复杂度分析

时间复杂度： ，该方法需要遍历树的所有结点 。

空间复杂度： ，该方法在递归时需要使用队列空间 。

我的代码

public class Solution {
    public class TreeNode {
        int val = 0;
        TreeNode left = null;
        TreeNode right = null;
        public TreeNode(int val) {
            this.val = val;
        }
    }
    //判断当前层是否对称
    boolean isCurLyerSymmetrical(ArrayList<Integer>list){
        int i=0;
        int j=list.size()-1;
        while(i<j){
            if(list.get(i).equals(list.get(j))){
                i++;j--;
            }
            else return false;
        }
        return true;
    }
    //层次遍历存储拿到每一层
    boolean isSymmetrical(TreeNode pRoot) {
        LinkedList<TreeNode>q=new LinkedList<>();
        ArrayList<Integer>list=new ArrayList<>();
        if(pRoot==null)return true;
        q.add(pRoot);
        while(!q.isEmpty()){
            int n=q.size();
            list.clear();
            TreeNode node=null;
            //拿到每一层的结点
            for(int i=0;i<n;i++){
                node=q.poll();
                if(node.left!=null){
                    q.add(node.left);
                    list.add(node.left.val);
                }else{
                    list.add(1001);            //表示当前结点的左孩子是null
                }
                if(node.right!=null){
                    q.add(node.right);
                    list.add(node.right.val);
                }else{
                    list.add(1001);            //表示当前结点的右孩子是null
                }
            }
            if(!isLyerSymmetrical(list))
                return false;
        }
        return true;
    }
}