最小路径覆盖总结

定义

在一个有向图中，找出最少的路径，使得这些路径经过了所有的点**

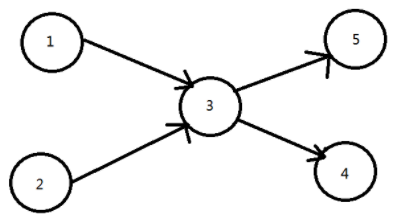
最小路径覆盖分为最小不相交路径覆盖和最小可相交路径覆盖

1. 最小不相交路径覆盖：每一条路径经过的顶点各不相同。如图，其最小路径覆盖数为3。
   • 即1->3>4，2，5
2. 最小可相交路径覆盖：每一条路径经过的顶点可以相同。如图，其最小路径覆盖数为2。
   • 即1->3->4，2->3>5

🍖匈利亚算法传送门
**
https://www.yuque.com/qingxuan-u4juc/tqfacc/qld036

有向无环图(DAG)的最小不相交路径覆盖

算法：
把原图的每个点 V 拆成 V**

证明：
一开始每个点都是独立的为一条路径，总共有 n 条不相交路径。我们每次在二分图里找一条匹配边就相当于把两条路径合成了一条路径，也就相当于路径数减少了 1 。所以找到了几条匹配边，路径数就减少了多少。所以有 最小路径覆盖 **= 原图的结点数 - **新图的最大匹配数

有向无环图(DAG)的最小可相交路径覆盖

算法：

1. 先用 floyd 求出原图的传递闭包，即如果 a 到 b 有路径，那么就加边a->b
2. 然后就转化成了最小不相交路径覆盖问题

证明：
为了连通两个点，某条路径可能经过其它路径的中间点。比如1->3->4，2->4->5 。但是如果两个点 a 和 b是连通的，只不过中间需要经过其它的点，那么可以在这两个点之间加边，那么 a 就可以直达 b ，不必经过中点的，那么就转化成了最小不相交路径覆盖。