[LeetCode]Ar645. 错误的集合

🚩传送门：https://leetcode-cn.com/problems/set-mismatch/

题目

集合 s 包含从 1 到 n 的整数。不幸的是，因为数据错误，导致集合里面某一个数字复制了成了集合里面的另外一个数字的值，导致集合 丢失了一个数字 并且 有一个数字重复 。

给定一个数组 nums 代表了集合 S 发生错误后的结果。找出重复出现以及丢失的整数，以数组的形式返回。

示例 1：

输入：nums = [1,2,2,4] 输出：[2,3]

示例 2：

输入：nums = [1,1] 输出：[1,2]

解题思路：排序

将数组排序之后，比较每对相邻的元素，如果相邻的两个元素相等，则该元素为重复的数字 。
寻找丢失的数字相对复杂，可能有以下两种情况：

1. 如果丢失的数字大于 1 且小于 n，则存在相邻的两个元素的差为 2，这两个元素之间的值为丢失的数字；
2. 如果丢失的数字是 1 或 n，则需要另外判断。

复杂度分析

时间复杂度：，其中 是 的长度。

排序需要 ，遍历数组找到错误元素需要 的时间，因此总时间复杂度是

空间复杂度：或 ，其中 是 的长度。

根据不同的排序需要或 的空间。

😱我的代码

class Solution {
    public int[] findErrorNums(int[] nums) {
        //1.定义错误数组
        int[] errorNums = new int[2];
        int n = nums.length;
        //2.将nums数组排序
        Arrays.sort(nums);
        //3.依次遍历排序后的nums数组
        for (int i = 1; i < n; i++) {
            //4.当前数等于上一个数,此乃重复数字
            if (nums[i]==nums[i-1]) {
                errorNums[0] = nums[i];
            } 
            //5.差值为2,中间乃缺失数字
            else if (nums[i] - nums[i-1] > 1) {
                errorNums[1] = nums[i] - 1;
            }
        }
        //6.预防第一个不是1
        if(nums[0]!=1){
            errorNums[1] = 1; 
        }
        //7.预防最后一个不是n
        if (nums[n - 1] != n) {
            errorNums[1] = n;
        }
        //8.返回答案数组
        return errorNums;
    }
}

解题思路：哈希表

重复的数字在数组中出现 2 次，丢失的数字在数组中出现 0 次，其余的每个数字在数组中出现 1 次。因此可以使用哈希表记录每个元素在数组中出现的次数，然后遍历从 1 到 n 的每个数字，分别找到出现 2 次和出现 0 次的数字，即为重复的数字和丢失的数字。

复杂度分析

时间复杂度：，其中 是 的长度。

需要遍历数组并填入哈希表，然后遍历从 1 到 n 的每个数寻找错误的集合。

空间复杂度： ，其中 是 的长度。

需要创建大小为 的哈希表。

官方代码

class Solution {
    public int[] findErrorNums(int[] nums) {
        //1.返回答案数组
        int[] errorNums = new int[2];
        int n = nums.length;
        //2.查找的map集合
        Map<Integer, Integer> map = new HashMap<Integer, Integer>();
        //3.依次遍历存入map
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        //4.依次遍历查找元素为0或2的元素
        for (int i = 1; i <= n; i++) {
            int count = map.getOrDefault(i, 0);
            //5.重复元素
            if (count == 2) {
                errorNums[0] = i;
            } 
            //6.缺失元素
            else if (count == 0) {
                errorNums[1] = i;
            }
        }
        //7.返回结果集合
        return errorNums;
    }
}

解题思路：位运算 [老熟人😗异或]

使用位运算，可以达到 的时间复杂度和 的空间复杂度。

异或运算：即两个输入相同时为0，不同则为1

1. 归零律：
2. 恒等律：
3. 交换律：
4. 结合律：
5. 自反：

重复的数字在数组中出现 2 次，丢失的数字在数组中出现 0 次，其余的每个数字在数组中出现 1 次。
如果在数组的 n 个数字后面再添加从 1 到 n 的每个数字，得到 2n 个数字，则在 2n 个数字中，重复的数字出现 3 次，丢失的数字出现 1 次，其余的每个数字出现 2 次。可以使用异或运算求解。

异或出来的结果必然是：重复数字( x ) ⊕ 缺失数字( y )

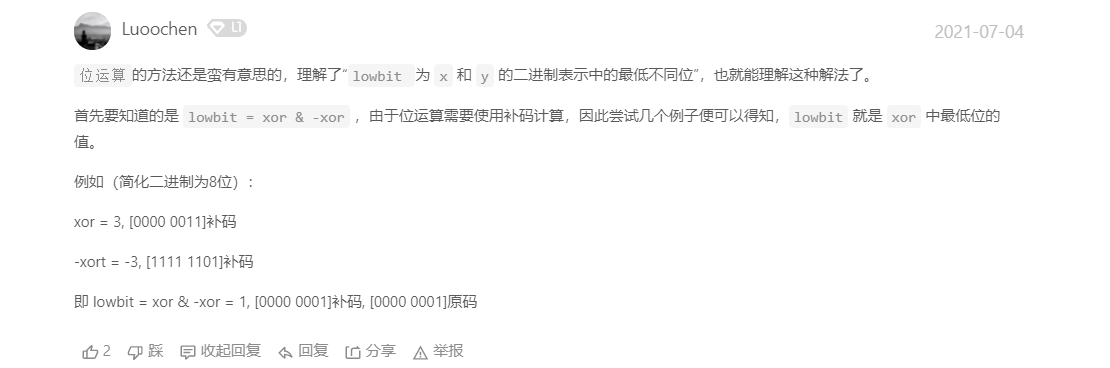
位运算的方法还是蛮有意思的，理解了“lowbit 为 x 和 y 的二进制表示中的最低不同位”，也就能理解这种解法了。
首先要知道的是 lowbit = xor & -xor ，由于位运算需要使用补码计算，因此尝试几个例子便可以得知，lowbit 就是 xor 中最低位的值。
例如（简化二进制为8位）：
xor = 3, [0000 0011]补码
-xort = -3, [1111 1101]补码
即 lowbit = xor & -xor = 1, [0000 0001]补码, [0000 0001]原码

• 解三真的牛批,说下自己看后的理解吧.
• 首先分析lowbit方法,这个是用来获取一个数最低位1的,而lowbit(x^y),因为是异或运算,所以当x^y的某一位为1时,x和y一定是一个0和一个1,因此lowbit(x^y)就是获取到x和y不同位中最低的一个(其实获取任意一个都行,但最低位好获取)
• 分组可以说是这道题的精髓了,按刚刚获取到的那一位分组,因为该位x和y一定是一个0一个1,所以可以确保他们被分到不同组.
• 之后就是都知道的了,因为x和y出现奇数次,而其余出现偶数次,在进行完全部异或运算后两组最后的数一定是一个x一个y,然后遍历扫一遍就行.

2踩回复

👀解题思路：数学

快不快不知道，但是优雅

1. 第一个元素：重复元素 = 当前数组和 - 去重后的数组和
2. 第二个元素：缺失元素 = 1至n求和 - 去重后的数组和

   大佬代码

   class Solution {
    public int[] findErrorNums(int[] nums) {
        return new int[] {
               Arrays.stream(nums).sum() - Arrays.stream(nums).distinct().sum(),
            (1 + nums.length) * nums.length / 2 - Arrays.stream(nums).distinct().sum()
        };
    }
   }