基本概念
科普下,最长公共子序列()和最长公共子串(
)不是一回事儿。
什么是子序列、子串呢?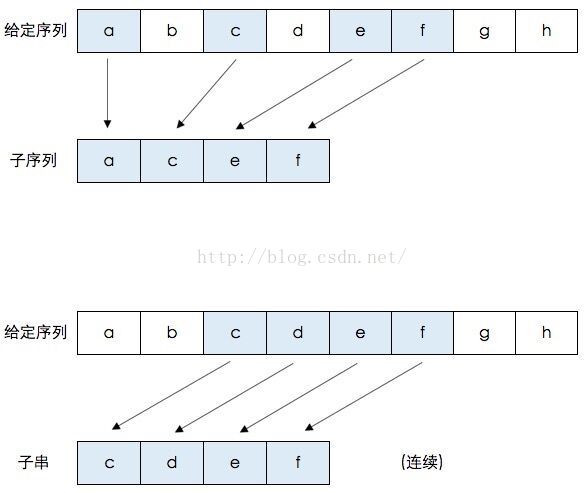
解回文子串:暴力搜索
根据回文子串的定义,枚举所有长度大于等于 的子串,依次判断它们是否是回文。
在具体实现时,可以只针对大于 “当前得到的最长回文子串长度” 的子串进行 “回文验证” 。
我的代码 [子串长度、具体子串]
public class Solution {public String longestPalindrome(String s) {int len = s.length();if (len < 2) return s;int maxLen = 1;String res = s.substring(0, 1);// 枚举所有长度大于等于 2 的子串for (int i = 0; i < len - 1; i++) {for (int j = i + maxLen; j < len; j++) {if (valid(s, i, j)) {maxLen = j - i + 1;//截取[i,j+1)res = s.substring(i, j + 1);}}}return res;}private boolean valid(String s, int left, int right) {// 验证子串 s[left, right] 是否为回文串while (left < right) {if (s.charAt(left) != s.charAt(right)) {return false;}left++;right--;}return true;}}
解回文子串:动态规划
- 一个字符一定是回文串
- 两个字符相等是回文串
- 长度大于
,那么将它首尾的两个字母去除之后,它仍然是个回文串。
例如对于字符串 “ababa’‘,若已知 “bab” 是回文串,那么 “ababa” 一定是回文串,因为它首尾两个字母相等
👉 定义: 表示
的第
个字符到第
个字符组成的串(下文表示成
)是否为回文串。
dp[i][j] 可以存放长度,若值 0 则非回文,非 0 值则回文 dp[i][j] 可以存放序列,若空串 “” 则非回文,非空串则回文
状态转移方程:
复杂度分析
时间复杂度: ,其中
分别是字符串的长度。
- 动态规划的状态总数为  ,对于每个状态,我们需要转移的时间为  。
空间复杂度:
- 即存储动态规划状态需要的空间。
我的代码 [子串长度、具体子串]
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) return s;
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i..j] 是否是回文串
boolean[][] dp = new boolean[len][len];
// 初始化:所有长度为 1 的子串都是回文串
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
char[] charArray = s.toCharArray();
// 先枚举子串长度
for (int L = 2; L <= len; L++) {
// 枚举左边界,左边界的上限设置可以宽松一些
for (int i = 0; i < len; i++) {
// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
int j = L + i - 1;
// 如果右边界越界,就可以退出当前循环
if (j >= len) break;
if (charArray[i] != charArray[j]) dp[i][j] = false;
else {
if (L==2) dp[i][j] = true;
else dp[i][j] = dp[i + 1][j - 1];
}
// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if (dp[i][j]) {
maxLen =L;
begin = i;
}
}
}
return s.substring(begin, begin + maxLen);
}
}
解回文子串:中心扩展
我们仔细观察一下方法一中的状态转移方程:
找出其中的状态转移链:
可以发现,我们可以从每一种边界情况开始「扩展」,也可以得出所有的状态对应的答案。
边界情况即为子串长度为 或
的情况。
我们枚举每一种边界情况,并从对应的子串开始不断地向两边扩展。
- _如果两边的字母相同,我们就可以继续扩展,例如从 _
- _如果两边的字母不同,我们就可以停止扩展,因为在这之后的子串都不能是回文串了。_
本质即为:我们枚举所有的「回文中心」并尝试「扩展」,直到无法扩展为止,此时的回文串长度即为此「回文中心」下的最长回文串长度。
我们对所有的长度求出最大值,即可得到最终的答案。
复杂度分析
时间复杂度: ,其中
分别是字符串的长度。
- 长度为  或  的回文中心分别有  和  个,每个回文中心最多会向外扩展  次。
空间复杂度:
我的代码 [具体序列]
class Solution {
public String longestPalindrome(String s) {
if (s == null || s.length() < 1) return "";
int start = 0, end = 0;
for (int i = 0; i < s.length(); i++) {
int len1 = expandAroundCenter(s, i, i);
int len2 = expandAroundCenter(s, i, i + 1);
int len = Math.max(len1, len2);
if (len > end - start) {
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substring(start, end + 1);
}
public int expandAroundCenter(String s, int left, int right) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
--left;
++right;
}
return right - left - 1;
}
}
解题回文子序列:动态规划
👉 定义: 表示
的第
个字符到第
个字符组成的子串中,最长的回文序列长度是多少。
状态转移方程:
注意遍历顺序, 从最后一个字符开始往前遍历,
从
开始往后遍历
初始化 单个字符的最长回文序列是
结果
我的代码 [序列长度]
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length();
int[][] dp = new int[n][n];
for (int i = n - 1; i >= 0; i--) {
//1. 单独必然构成回文
dp[i][i] = 1;
for (int j = i + 1; j < n; j++) {
if (s.charAt(i) == s.charAt(j))
dp[i][j] = dp[i + 1][j - 1] + 2;
else
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
return dp[0][n - 1];
}
}
我的代码 [具体序列]
class Solution {
public String longestPalindromeSubseq(String s) {
if(s==null||"".equals(s)||s.length()==0)return "";
int n = s.length();
String[][] dp = new String[n][n];
for (int i = n - 1; i >= 0; i--) {
dp[i][i] = s.charAt(i)+"";
for (int j = i + 1; j < n; j++) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = s.charAt(i)+dp[i + 1][j - 1] +s.charAt(i);
} else {
dp[i][j] =dp[i + 1][j].length()> dp[i][j - 1].length()?dp[i + 1][j]:dp[i][j - 1];
}
}
}
return dp[0][n - 1];
}
}

