🚩传送门：牛客题目

题目

请实现两个函数，分别用来序列化和反序列化二叉树。

你需要设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

示例：
[NC]123. 序列化二叉树 - 图1

输入：root = [1,2,3,null,null,4,5] 输出：[1,2,3,null,null,4,5]

解题思路1：广度优先搜索

通常使用的前序、中序、后序、层序遍历记录的二叉树的信息不完整，即唯一的输出序列可能对应着多种二叉树可能性。题目要求的 序列化 和 反序列化 是 可逆操作 。因此，序列化的字符串应携带 完整的二叉树信息 。

观察题目示例，序列化的字符串实际上是二叉树的 “层序遍历”（BFS）结果，本文也采用层序遍历。

为完整表示二叉树，考虑将叶节点下的 null 也记录。在此基础上，对于列表中任意某节点 node ，其左子节点 node.left 和右子节点 node.right 在序列中的位置都是 唯一确定 的。如下图所示：

详情参考堆的物理性在数组中的下标表示

[NC]123. 序列化二叉树 - 图2
序列化 使用层序遍历实现。反序列化 通过以上递推公式反推各节点在序列中的索引，进而实现。

🚩序列化 Serialize ：

借助队列，对二叉树做层序遍历，并将越过叶节点的 null 也打印出来。

🚩反序列化 Deserialize ：

基于本文开始推出的 node , node.left , node.right 在序列化列表中的位置关系，可实现反序列化。

利用队列按层构建二叉树，借助一个指针 i 指向节点 node 的左、右子节点，每构建一个 node 的左、右子节点，指针 i 就向右移动 1 位 。

复杂度分析

时间复杂度：[NC]123. 序列化二叉树 - 图3，其中 [NC]123. 序列化二叉树 - 图4 为二叉树结点个数。

  1.   - 序列化阶段：  ![](https://cdn.nlark.com/yuque/__latex/7b8b965ad4bca0e41ab51de7b31363a1.svg#card=math&code=n%20%20&id=kd6wZ) 个二叉树结点个数，层序遍历需要访问所有节点，个数总是为 ![](https://cdn.nlark.com/yuque/__latex/d2b2d9fec288403faf6e85ebf2c58972.svg#card=math&code=2n%2B1&id=BT5av)  ，总体复杂度为 ![](https://cdn.nlark.com/yuque/__latex/32e4086c0f5de136085846505396eae1.svg#card=math&code=O%282n%20%2B%201%29%20%3D%20O%28n%29&id=NcuhR)。
  3.   -  反序列化阶段：![](https://cdn.nlark.com/yuque/__latex/7b8b965ad4bca0e41ab51de7b31363a1.svg#card=math&code=n%20%20&id=khVbI) 个二叉树结点个数，按层构建二叉树需要遍历整个 **vals**，长度最大为 ![](https://cdn.nlark.com/yuque/__latex/d2b2d9fec288403faf6e85ebf2c58972.svg#card=math&code=2n%2B1&id=NBb1c)

空间复杂度：[NC]123. 序列化二叉树 - 图5，其中 [NC]123. 序列化二叉树 - 图6 为二叉树结点个数。

  1.   - 序列化阶段： ![](https://cdn.nlark.com/yuque/__latex/7b8b965ad4bca0e41ab51de7b31363a1.svg#card=math&code=n%20%20&id=sr0bQ) 个二叉树结点个数，最差情况下，队列 **queue** 同时存储 ![](https://cdn.nlark.com/yuque/__latex/5c22c7cdc7ee39233eaa507d5962a417.svg#card=math&code=%5Cfrac%7Bn%20%2B%201%7D%7B2%7D%20&id=RSxp8) 个节点 。
  2.   -  反序列化阶段： ![](https://cdn.nlark.com/yuque/__latex/7b8b965ad4bca0e41ab51de7b31363a1.svg#card=math&code=n%20%20&id=bQ9G6) 个二叉树结点个数，最差情况下，队列 **queue** 同时存储 ![](https://cdn.nlark.com/yuque/__latex/5c22c7cdc7ee39233eaa507d5962a417.svg#card=math&code=%5Cfrac%7Bn%20%2B%201%7D%7B2%7D%20&id=OPhlB) 个节点 。

官方代码

  1. public class Codec {
  2.     public String serialize(TreeNode root) {
  3.         if(root == null) return "[]";
  4.         StringBuilder res = new StringBuilder("[");
  5.         Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }};
  6.         while(!queue.isEmpty()) {
  7.             TreeNode node = queue.poll();
  8.             if(node != null) {
  9.                 res.append(node.val).append(",");
  10.                 queue.add(node.left);
  11.                 queue.add(node.right);
  12.             }
  13.             else res.append("null,");
  14.         }
  15.         res.deleteCharAt(res.length() - 1);
  16.         res.append("]");
  17.         return res.toString();
  18.     }
  20.     // "[1,2,3,null,null,4,5]"
  21.     public TreeNode deserialize(String data) {
  22.         if(data.equals("[]")) return null;
  23.         String[] vals = data.substring(1, data.length() - 1).split(",");
  24.         TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
  25.         Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }};
  26.         int i = 1;
  27.         while(!queue.isEmpty()) {
  28.             TreeNode node = queue.poll();
  29.             if(!vals[i].equals("null")) { // 左子树不空
  30.                 node.left = new TreeNode(Integer.parseInt(vals[i]));
  31.                 queue.add(node.left);
  32.             }
  33.             i++;
  34.             if(!vals[i].equals("null")) { // 右子树不空
  35.                 node.right = new TreeNode(Integer.parseInt(vals[i]));
  36.                 queue.add(node.right);
  37.             }
  38.             i++;
  39.         }
  40.         return root;
  41.     }
  42. }

解题思路2：深度优先搜索 [线序为例]

二叉树的序列化本质上是对其值进行编码，更重要的是对其结构进行编码。可以遍历树来完成上述任务。

深度优先搜索可以从一个根开始，一直延伸到某个叶，然后回到根，到达另一个分支。根据根节点、左节点和右节点之间的相对顺序，可以进一步将深度优先搜索策略区分为：先序遍历、中序遍历、后序遍历

这里，我们选择先序遍历的编码方式做序列化，我们可以通过这样一个例子简单理解：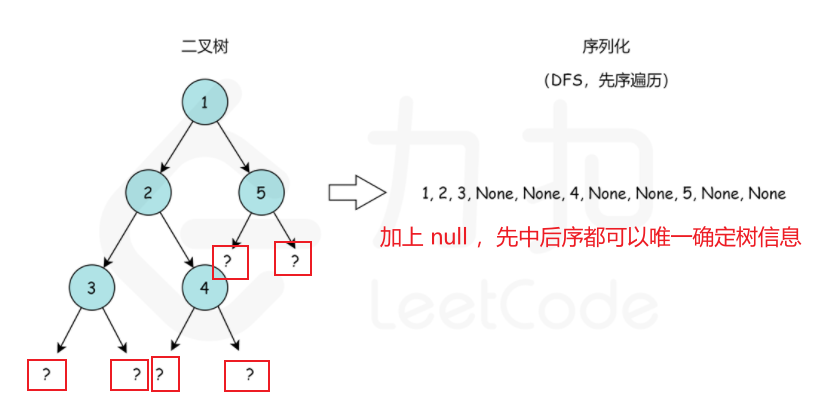
image.png
那么我们如何反序列化呢？

首先我们需要根据,把原先的序列分割开来得到先序遍历的元素列表，然后从左向右遍历这个序列：

  • 如果当前的元素为 None，则当前为空树
  • 否则先解析这棵树的左子树，再解析它的右子树

复杂度分析

时间复杂度：[NC]123. 序列化二叉树 - 图8，其中 [NC]123. 序列化二叉树 - 图9 为二叉树结点个数。

  1.   - 在序列化和反序列化函数中，我们只访问每个节点一次，因此时间复杂度为 ![](https://cdn.nlark.com/yuque/__latex/7ba55e7c64a9405a0b39a1107e90ca94.svg#card=math&code=O%28n%29%20&height=23&id=A4JUm)


空间复杂度：[NC]123. 序列化二叉树 - 图10，其中 [NC]123. 序列化二叉树 - 图11 为二叉树结点个数。

  1.   - 在序列化和反序列化函数中，我们递归会使用栈空间，故渐进空间复杂度为 ![](https://cdn.nlark.com/yuque/__latex/7ba55e7c64a9405a0b39a1107e90ca94.svg#card=math&code=O%28n%29%20&height=23&id=CXWFc)

官方代码

  1. public class Codec {
  2.     public String serialize(TreeNode root) {
  3.         StringBuilder res = new StringBuilder("");
  4.         return rserialize(root, res).toString();
  5.     }
  7.    public TreeNode deserialize(String data) {
  8.         String[] dataArray = data.split(",");
  9.         List<String> dataList = new LinkedList<String>(Arrays.asList(dataArray));
  10.         return rdeserialize(dataList);
  11.     }
  13.     public StringBuilder rserialize(TreeNode root, StringBuilder str) {
  14.         if (root == null) {
  15.             str.append("None,");
  16.         } else {
  17.             str.append(root.val).append(",");
  18.             str = rserialize(root.left, str);
  19.             str = rserialize(root.right, str);
  20.         }
  21.         return str;
  22.     }
  24.     public TreeNode rdeserialize(List<String> dataList) {
  25.         if (dataList.get(0).equals("None")) {
  26.             dataList.remove(0);
  27.             return null;
  28.         }
  30.         TreeNode root = new TreeNode(Integer.valueOf(dataList.get(0)));
  31.         dataList.remove(0);
  32.         root.left = rdeserialize(dataList);
  33.         root.right = rdeserialize(dataList);
  35.         return root;
  36.     }
  37. }