🚩[NC]94. 设计LFU缓存结构 【双向链表 双 HashMap】

🚩传送门：牛客题目

题目

请你为 最不经常使用（LFU）缓存算法设计并实现数据结构。实现 LFUCache 类：

**LFUCache(int capacity)** ：用数据结构的容量 capacity 初始化对象
**int get(int key)** ：如果键 key 存在于缓存中，则获取键的值，否则返回 -1 。
**void put(int key, int value)** ：如果键 key 已存在，则变更其值，如果键不存在，请插入键值对。当缓存达到其容量 capacity 时，则应该在插入新项之前，移除最不经常使用的项。当存在平局（即两个或更多个键具有相同使用频率）时，应该去除 最近最久未使用 的键。

为了确定最不常使用的键，可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。

当一个键首次插入到缓存中时，它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作，使用计数器的值将会递增。

🚩 注意：函数 get 和 put 必须以 的平均时间复杂度运行。

解题思路：双向链表 O( n)

最傻fufu の 解法

链表排序准则优先按照 freq 排序，当 freq 相等时，按照时间戳排序，时间久的排前面，创建时间端，因此满了之后删除 head.post，该 Node 即 freq 最小且最久访问的。

每次 node 的 freq++ 后，从当前位置向后遍历链表，直到 nextNode.freq > node.freq || nextNode == tail，在 nextNode 之前插入该 node。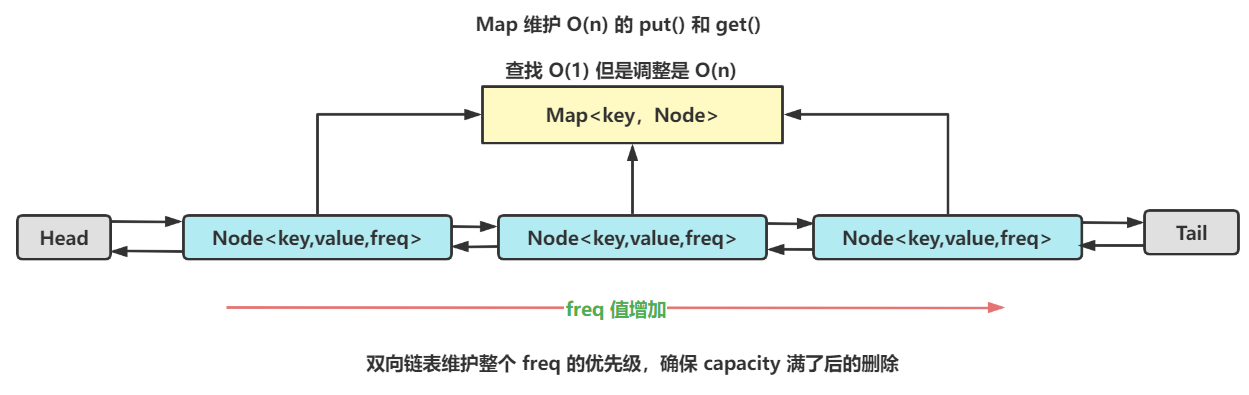

复杂度分析

时间复杂度：，其中 指的是 capacity 大小。

空间复杂度：，其中 指的是 capacity 大小。

官方代码

// 双向链表结点类
class Node {
    int key;
    int value;
    int freq = 1;
    Node pre;
    Node post;
    public Node() {}
    public Node(int key, int value) {
        this.key = key;
        this.value = value;
    }
}
// LFU 缓存类
class LFUCache {
    // Map 缓存 <key,Node>
    HashMap<Integer, Node> cache;
    Node head;
    Node tail;
    int capacity;
    int size;
    // 初始化
    public LFUCache(int capacity) {
        cache = new HashMap<Integer, Node>(capacity);
        this.capacity = capacity;
        head = new Node();
        tail = new Node();
        head.post = tail;
        tail.pre = head;
    }
    // 获取
    public int get(int key) {
        Node node = cache.get(key);
        if (node == null) {
            return -1;
        }
        node.freq++;
        moveToNewPosition(node);
        return node.value;
    }
    public void put(int key, int value) {
        if (capacity == 0) {
            return;
        }
        Node node = cache.get(key);
        // 插入 <key,value> 在缓存中,则热度增加,重新排序
        if (node != null) {
            node.value = value;
            node.freq++;
            moveToNewPosition(node);
        } else {
            // 插入 <key,value> 不在缓存中,查看容量是否满了
            if (size == capacity) {
                // 满了移除热度最小最久的 node
                cache.remove(head.post.key);
                removeNode(head.post);
                size--;
            }
            // 重新添加新的 node
            Node newNode = new Node(key, value);
            addNode(newNode);
            cache.put(key, newNode);
            size++;
        }
    }
    private void moveToNewPosition(Node node) {
        Node nextNode = node.post;
        removeNode(node);
        while (nextNode.freq <= node.freq && nextNode != tail) {
            nextNode = nextNode.post;
        }
        nextNode.pre.post = node;
        node.pre = nextNode.pre;
        node.post = nextNode;
        nextNode.pre = node;
    }
    private void addNode(Node node) {
        node.post = head.post;
        node.pre = head;
        head.post.pre = node;
        head.post = node;
        moveToNewPosition(node);
    }
    private void removeNode(Node node) {
        node.pre.post = node.post;
        node.post.pre = node.pre;
    }
}

解题思路：优先队列、最小堆 O( logN)

将访问频次 freq 最小的且最先访问的上浮到堆顶，下面用 idx = System.currentTimeMillis() 比较访问时间的先后。

若全局自增 idx 表示访问的先后，一旦溢出就 BUG 了

复杂度分析

时间复杂度：，其中 指的是 capacity 大小。

空间复杂度：，其中 指的是 capacity 大小。

官方代码

class Node {
    int key, val, freq;
    Node(int key, int val, int freq) {
        this.key = key;
        this.val = val;
        this.freq = freq;
    }
}
class LFUCache {
    Map<Integer, Node> cache;    // Map 做缓存用于 O(logN) Put 和 Get
    Queue<Node> queue;            // 优先队列做排序结构
    int capacity;
    int size;
    int idx = 0;
    public LFUCache(int capacity) {
        cache = new HashMap<>(capacity);
        if (capacity > 0) {
            queue = new PriorityQueue<>(capacity);    // 定义 capacity 容量的最小堆
        }
        this.capacity = capacity;
    }
    public int get(int key) {
        Node node = cache.get(key);
        if (node == null) {
            return -1;
        }
        node.freq++;
        node.idx = System.currentTimeMillis();
        queue.remove(node);
        queue.offer(node);
        return node.value;
    }
    public void put(int key, int value) {
        if (capacity == 0) {
            return;
        }
        Node node = cache.get(key);
        if (node != null) {
            // 当前 <key,value> 已经被缓存
            node.value = value;
            node.freq++;
            node.idx = System.currentTimeMillis();
            queue.remove(node);
            queue.offer(node);
        } else {
            // 当前 <key,value> 未被缓存,且满容量 
            if (size == capacity) {
                cache.remove(queue.peek().key);        // 缓存中移除最小最久热度
                queue.poll();                        // 结构中移除最小最久热度
                size--;
            } 
            Node newNode = new Node(key, value, System.currentTimeMillis());
            cache.put(key, newNode);                // 缓存中添加最新热度结点
            queue.offer(newNode);                    // 结构中添加最新热度结点
            size++;
        }
    }
}
class Node implements Comparable<Node> {
    int key;
    int value;
    int freq;
    int idx;
    public Node() {}
    public Node(int key, int value, int idx) {
        this.key = key;
        this.value = value;
        freq = 1;
        this.idx = idx;
    }
    // 比较准则:优先比较频率,频率相同比较时间戳
    public int compareTo(Node node) {
        int diff = freq - node.freq;
        return diff != 0? diff: idx - node.idx;
    }
}

解题思路：双HashMap、自写双向链表 Remove（地址删除） O(1)

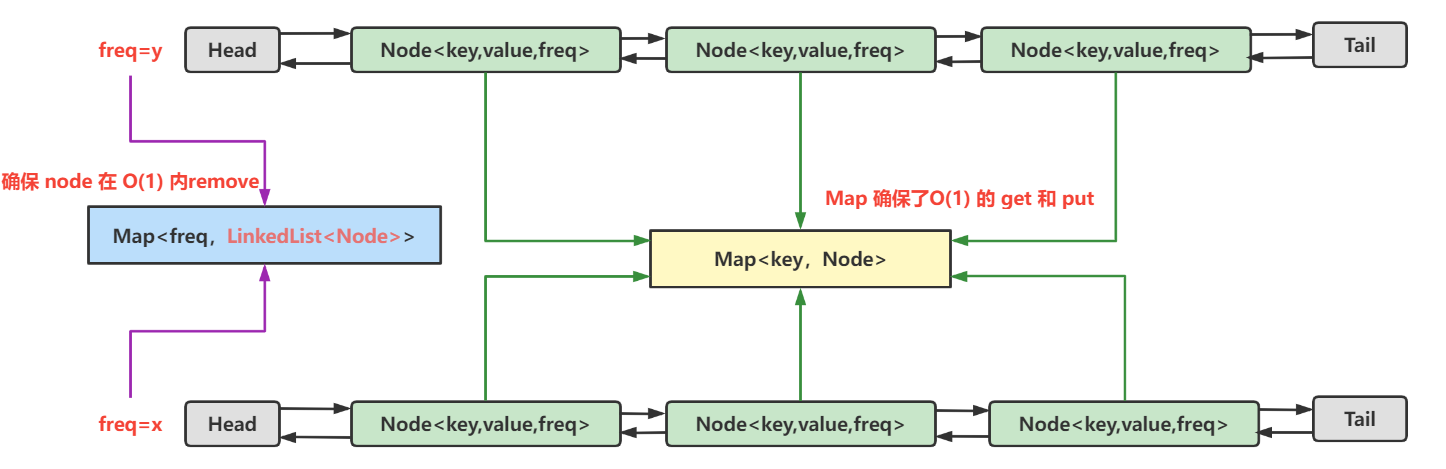
对于具有相同的 freq 的 Node ，新 Node 在双向链表中使用头插法，因此链表的尾部则是最久不使用的。
由于 LinkedList 的 remove 删除是 ，因此想让 get、put 在 内，需要自己写 remove（地址） 。

注意：用官方的 LinkedList 实现的双向链表不是 而是 ，其 remove 函数是顺序查找，非按地址删除

复杂度分析

时间复杂度：，所有的操作均在 内完成 。

空间复杂度：，其中 指的是 capacity 大小。

官方代码

class Node {
    int key;
    int value;
    int freq ;    // 保存频率
    Node pre;   // Node所在频次的双向链表的前继Node
    Node post;  // Node所在频次的双向链表的后继Node
    public Node() {
        freq = 1;    // 无参构造函数默认创建频率 1
    }
    public Node(int key, int value,int freq) {
        this.key = key;
        this.value = value;
        this.freq = freq;
    }
}
class DoublyLinkedList {
    Node head;               // 该双向链表的头节点，新节点从头部加入，表示最近访问
    Node tail;               // 该双向链表的尾节点，删除节点从尾部删除，表示最久访问
    int capacity;
    public DoublyLinkedList() {
        capacity=0;             // 初始化容量为 0
        head = new Node();
        tail = new Node();
        head.post = tail;
        tail.pre = head;
    }
    int size(){
        return capacity;
    }
    Node peekFirst() {  // 返回首结点不删除
        if (head.post != tail)
            return head.post;
        return null;
    }
    Node pollFirst() {  // 返回首结点删除
        Node node=null;
        if (head.post != tail){
            node = new Node(head.post.key,head.post.value,head.post.freq);
            remove(head.post);
        }
        return node;
    }
    Node peekLast() {
        if (tail.pre != head)
            return tail.pre;
        return null;
    }
    Node pollLast() {
        Node node=null;
        if (tail.pre != head){
            node = new Node(tail.pre.key,tail.pre.value,tail.pre.freq);
            remove(tail.pre);
        }
        return node;
    }
    void remove(Node node) {
        if(node==null||capacity==0) return;
        node.pre.post = node.post;
        node.post.pre = node.pre;
        capacity--;
    }
    // 头插法
    void addNode(Node node) {
        node.post = head.post;
        head.post.pre = node;
        head.post = node;
        node.pre = head;
        capacity++;
    }
}
class LFUCache {
    int minfreq, capacity;
    Map<Integer, Node> key_table;
    Map<Integer, DoublyLinkedList> freq_table;
    public LFUCache(int capacity) {
        this.minfreq = 0;
        this.capacity = capacity;
        key_table = new HashMap<Integer, Node>();                // 维护O(1)查找、插入
        freq_table = new HashMap<Integer, DoublyLinkedList>();    // 维护删除过时结构
    }
    public int get(int key) {
        if (capacity == 0) {
            return -1;
        }
        if (!key_table.containsKey(key)) {
            return -1;
        }
        Node node = key_table.get(key);
        int val = node.value, freq = node.freq;
        freq_table.get(freq).remove(node);                        // 在O(1)内删除结点
        // 如果当前链表为空，我们需要在哈希表中删除，且更新minFreq
        if (freq_table.get(freq).size() == 0) {
            freq_table.remove(freq);
            if (minfreq == freq) {
                minfreq++;
            }
        }
        // 插入到 freq + 1 中
        DoublyLinkedList list = freq_table.getOrDefault(freq + 1, new DoublyLinkedList());
        list.addNode(new Node(key, val, freq + 1));
        freq_table.put(freq + 1, list);
        key_table.put(key, freq_table.get(freq + 1).peekFirst());
        return val;
    }
    public void put(int key, int value) {
        if (capacity == 0) {
            return;
        }
        if (!key_table.containsKey(key)) {
            // 缓存已满，需要进行删除操作
            if (key_table.size() == capacity) {
                // 通过 minFreq 拿到 freq_table[minFreq] 链表的末尾节点
                Node node = freq_table.get(minfreq).peekLast();
                key_table.remove(node.key);
                freq_table.get(minfreq).pollLast();
                if (freq_table.get(minfreq).size() == 0) {
                    freq_table.remove(minfreq);
                }
            }
            DoublyLinkedList list = freq_table.getOrDefault(1, new DoublyLinkedList());
            list.addNode(new Node(key, value, 1));
            freq_table.put(1, list);
            key_table.put(key, freq_table.get(1).peekFirst());
            minfreq = 1;
        } else {
            // 与 get 操作基本一致，除了需要更新缓存的值
            Node node = key_table.get(key);
            int freq = node.freq;
            freq_table.get(freq).remove(node);
            if (freq_table.get(freq).size() == 0) {
                freq_table.remove(freq);
                if (minfreq == freq) {
                    minfreq++;  
                }
            }
            DoublyLinkedList list = freq_table.getOrDefault(freq + 1, new DoublyLinkedList());
            list.addNode(new Node(key, value, freq + 1));
            freq_table.put(freq + 1, list);
            key_table.put(key, freq_table.get(freq + 1).peekFirst());
        }
    }
}