红黑树总结

红黑树定义

它要么是一颗空树，要么是具有以下性质的二叉查找树

1. 根节点一定是黑的。
2. 插入的新节点一定是红色的 （若作为根服从根是黑色的）
3. 每个节点或是红的，或是黑的。
4. 每个叶节点（NIL）是黑的。（所有NULL结点称为叶子节点，且认为颜色为黑）
5. 如果一个节点是红的，则他的两个子节点是黑的。
6. 对每个节点，从该节点到其子孙节点的所有路径上包含相同数目的黑节点。

   红黑树插入

总结：

1. 🐛旋转操作与AVL树一样，只不过旋下来涂红，旋上去涂黑
2. 插入后，以刚插入的节点作为当前平衡节点N，进行平衡操作

3. 红结点要么没孩子，若有孩子一定是两个黑结点孩子

   解释：对每个结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点

4. 失衡一定是自己红，父亲红。

   • 这句话太绝对了所以这里备注一句吧：红黑树只是符合一些性质的树，故而没有绝对的谁对谁错。
   • 在老外部分书籍中自己红，父亲黑，兄弟红，定义为失衡，有的不定义为失衡，若定义失衡也很好处理，自己涂黑，兄弟涂黑，父亲涂红，父亲做N向上检查

   下面的话纯属个人心得所言，不一定正确，写着玩的，欢迎探讨斧正，但是客官可以尝试接受理解以下，看是否有道理。我认为两种方式从两种不同的角度考虑，没有谁对谁错之分，毕竟谁也不是正统。 定义失衡：有点学术角度的意思，因为它的的的确确应该被处理，越拖到后期，旋转次数越多，既然趁早发现了为什么不趁早处理点，要拖到后面呢是吧 。 不定义失衡：理由很简单，我东西是要给顾客使用的，在使用的过程中，当然是速度越快越好，体验感才好，若定义失衡，一旦处理，是需要向上检查是否失衡的，若一路失衡下去，处理速度会慢很多。虽然及时处理会提高后面的速度，但牺牲前面人的速度来提升后面人的速度，不知道……后面老哥愿不愿意…

   多讲一句，你一般接触的红黑树大部分此类情况都是定为不失衡的。

🚩现在回过头看插入平衡的这4种情形，其实并不复杂（其实就是双红冲突）：

情形一：N为根：涂黑完事
情形二：父黑：啥事不用管

情形三：父红叔红：父和叔涂黑，祖父涂红，然后把祖父当成新的平衡节点递归处理（我们下面平衡了，让他老人家和上面沟通吧）

备注：这种情况会出现就是因为自己红，父亲黑，兄弟红，定义为不失衡

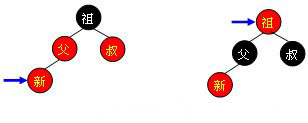
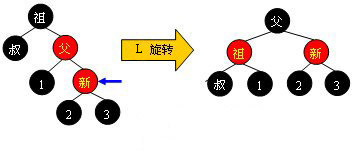
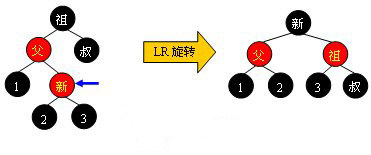
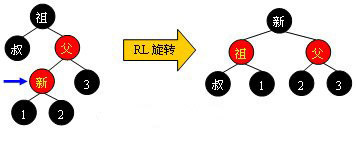
情形四：父红叔黑：父节点和新插入节点同一边的话，扭一下（单旋或者双旋），旋转上去结点涂黑，旋下来结点涂红，一共4类情形等下讨论

红黑树删除

为了方便说明，我们先约定一下节点名称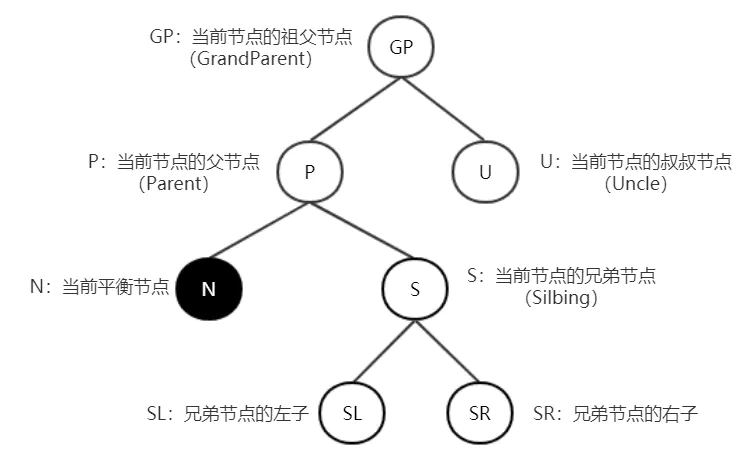

红黑树的节点删除基本也可以简单分为三种情况：

1. 删除点p的左右子树都为空 🚩情况最复杂、需要重点分析的
2. 删除点p的左右子树只有一棵子树非空
3. 删除点p的左右子树都非空

对于情况1，需要考虑删除结点的颜色，若红色直接删除，若黑色直接删除会失衡，因此需要fixAfterDeletion()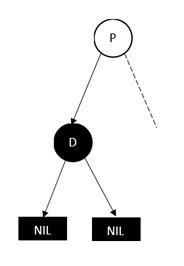

对于情况2，删除结点只有一棵子树非空，那么删除结点一定是BLACK，拥有唯一一个孩子是RED，
也需要fixAfterDeletion(D)

其实只是将孩子RED，涂黑、修改引用

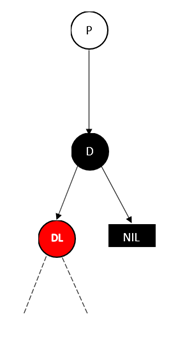
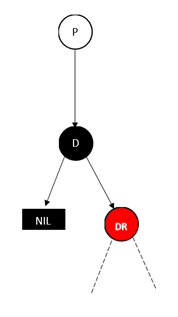
对于情况3，利用后继结点可以转化成情况1、情况2
首先请思考一下，删除了哪些点才会导致调整？
只有删除点是BLACK 结点的时候，才会触发调整函数，因为删除RED 结点不会破坏红黑树的任何约束，而删除BLACK节点会破坏规则4。

红黑树到所有叶子结点的黑色结点个数相同

跟上文中讲过的fixAfterInsertion()函数一样，这里也要分成若干种情况。记住，无论有多少情况，具体的调整操作只有两种:

1. 改变某些节点的颜色
2. 对某些节点进行旋转

🚩从上文我们知道，整个fixAfterInsertion()调整的就是删除的结点是黑色的情形，因此整个重点就是讲解黑色结点的删除，由于轴对称因此我们只讲解N是P的左子树，镜像操作类似。

情形一：兄弟节点是红色的

N 是BLACK，S是RED，那么父亲一定是BLACK，且S拥有SL，SR均是BLACK，SL or SR若有孩子只能是RED

step1：调整做法是将父亲节点和兄弟节点的颜色互换，也就是P变成红色，S变成黑色
step2：然后对P进行AVL树种的R操作，结果如下图
目的：成功将被删除结点的兄弟结点转换成黑色的，操作步骤如**情形2**所示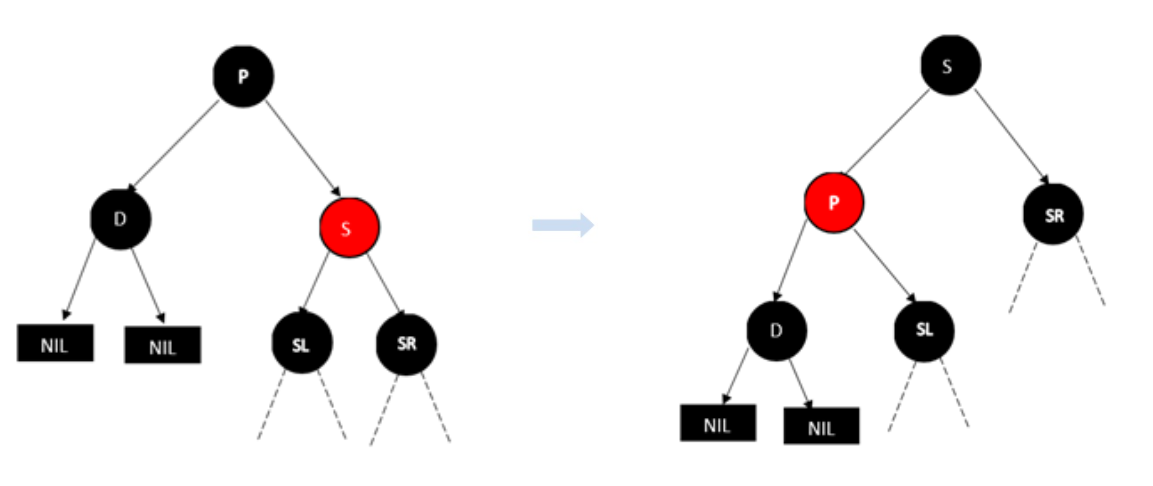

情形二：兄弟节点是黑色的

Tips：实际上父亲结点的颜色不重要，操作相同。讨论后会发现

2.1 兄弟节点是黑色的，且没有子节点
step1：将兄弟节点设置为红色，将父节点设置为当前节点递归，直到根节点，或遇到红色节点。


2.2 兄弟节点是黑色的，且有一个红色 L 子节点
step1：将左孩子设置为黑色。
step2：将兄弟节点设置为红色。
step3：对兄弟节点进行右旋。
step4：经过上述操作后，将情形2.2转化成了情形2.3的情况处理了。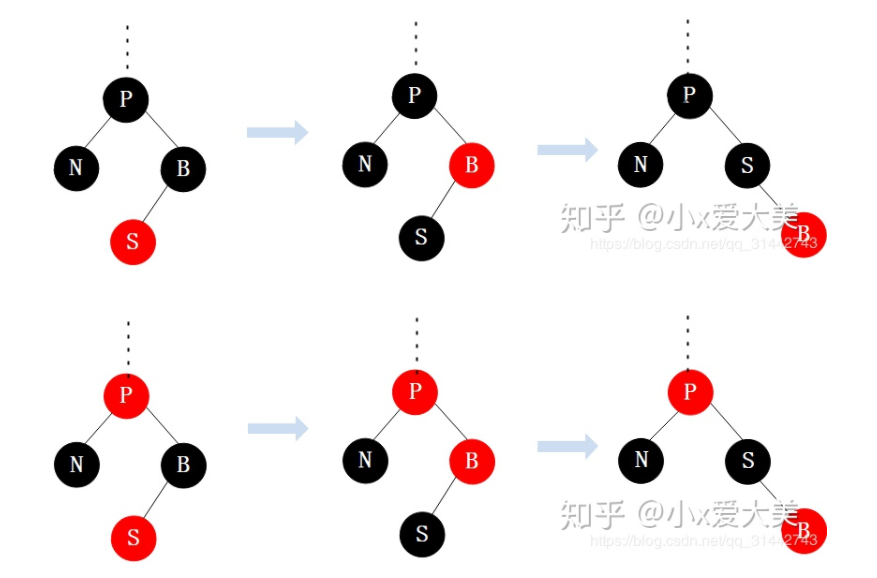

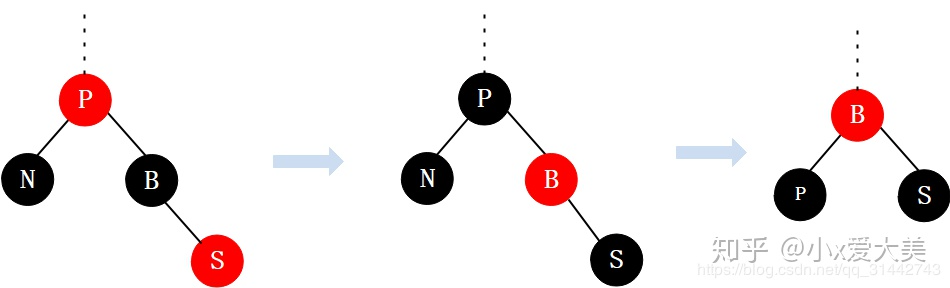
2.3 兄弟节点是黑色的，且有一个红色 R 子节点
step1：将父节点的颜色赋给兄弟节点。
step2：将兄弟节点的右孩子置为黑色。
step3：对父结点设置为黑色。
step4：对父节点进行左旋。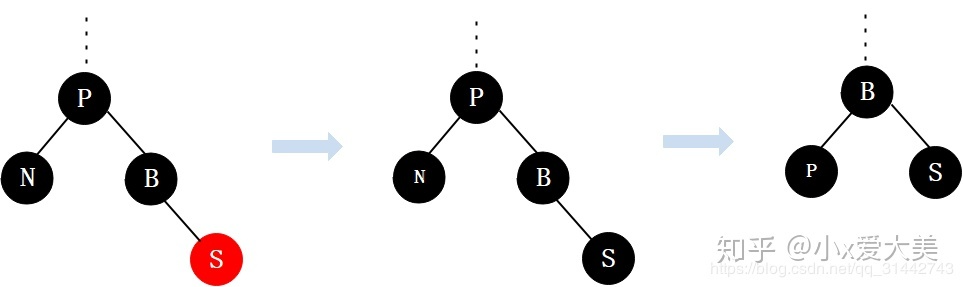


2.4 兄弟节点是黑色的，且有两个红色 L、R 子节点
step1：将父节点颜色赋给兄弟节点
step2：将兄弟节点的右孩子设置为黑色。
step3：对父节点设置为黑色
step4：对父节点进行左旋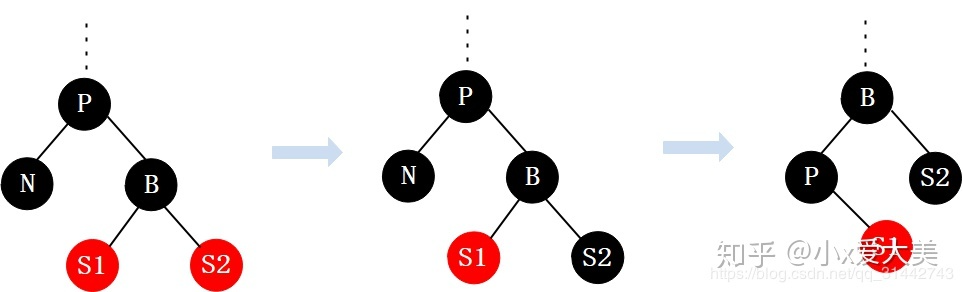


我们发现**情形2.3**``**情形2.4**操作完全一致，因此将这两种合并为同一种情形

private void fixAfterDeletion(Entry<K,V> x) {
    while (x != root && colorOf(x) == BLACK) {                        // 当前删除的结点是黑色
        if (x == leftOf(parentOf(x))) {                                // x 是p的左子树
            Entry<K,V> sib = rightOf(parentOf(x));                    // sib 是 x 的兄弟
            if (colorOf(sib) == RED) {                                // sib 是红色,则p一定是黑色,且sib有孩子,sibL、sibR为黑色
                setColor(sib, BLACK);                   // 情况1    
                setColor(parentOf(x), RED);             // 情况1        => 兄弟是红色的操作成兄弟是黑色的
                rotateLeft(parentOf(x));                // 情况1 
                sib = rightOf(parentOf(x));             // 情况1
            }
            if (colorOf(leftOf(sib))  == BLACK && colorOf(rightOf(sib)) == BLACK) {        // 兄弟没有孩子结点,性质NLP结点为黑色
                setColor(sib, RED);                     // 情况2.1    => 兄弟没有孩子结点
                x = parentOf(x);                        // 情况2.1
            } else {
                if (colorOf(rightOf(sib)) == BLACK) {                                    // 兄弟有红色左孩子(如果右孩子为NLP)
                    setColor(leftOf(sib), BLACK);       // 情况2.2
                    setColor(sib, RED);                 // 情况2.2
                    rotateRight(sib);                   // 情况2.2    => 兄弟有红色左孩子操作成红色右孩子
                    sib = rightOf(parentOf(x));         // 情况2.2
                }
                setColor(sib, colorOf(parentOf(x)));    // 情况2.3 、2.4
                setColor(parentOf(x), BLACK);           // 情况2.3 、2.4    => 兄弟有红色右孩子、兄弟有红色左右孩子操作相同
                setColor(rightOf(sib), BLACK);          // 情况2.3 、2.4
                rotateLeft(parentOf(x));                // 情况2.3 、2.4
                x = root;                               // 情况2.3 、2.4
            }
        } else { // 跟前四种情况对称
            Entry<K,V> sib = leftOf(parentOf(x));
            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);                   // 情况1镜像
                setColor(parentOf(x), RED);             // 情况1镜像
                rotateRight(parentOf(x));               // 情况1镜像
                sib = leftOf(parentOf(x));              // 情况1镜像
            }
            if (colorOf(rightOf(sib)) == BLACK && colorOf(leftOf(sib)) == BLACK) {
                setColor(sib, RED);                     // 情况2.1镜像
                x = parentOf(x);                        // 情况2.1镜像
            } else {
                if (colorOf(leftOf(sib)) == BLACK) {
                    setColor(rightOf(sib), BLACK);      // 情况2.2镜像
                    setColor(sib, RED);                 // 情况2.2镜像
                    rotateLeft(sib);                    // 情况2.2镜像
                    sib = leftOf(parentOf(x));          // 情况2.2镜像
                }
                setColor(sib, colorOf(parentOf(x)));    // 情况2.3 、2.4镜像
                setColor(parentOf(x), BLACK);           // 情况2.3 、2.4镜像
                setColor(leftOf(sib), BLACK);           // 情况2.3 、2.4镜像
                rotateRight(parentOf(x));               // 情况2.3 、2.4镜像
                x = root;                               // 情况2.3 、2.4镜像
            }
        }
    }
    setColor(x, BLACK);
}