🚩传送门：牛客题目

题目

给你一个 [NC]38. 螺旋矩阵/顺时针打印数组 - 图1 行[NC]38. 螺旋矩阵/顺时针打印数组 - 图2列的矩阵 [NC]38. 螺旋矩阵/顺时针打印数组 - 图3，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：
[NC]38. 螺旋矩阵/顺时针打印数组 - 图4

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[1,2,3,6,9,8,7,4,5]

解题思路：模拟

可以模拟螺旋矩阵的路径。

初始位置是矩阵的左上角，初始方向是向右，当路径超出界限或者进入之前访问过的位置时，顺时针旋转，进入下一个方向。

如何判断路径是否进入之前访问过的位置？
需要使用一个与输入矩阵大小相同的辅助矩阵 [NC]38. 螺旋矩阵/顺时针打印数组 - 图5，其中的每个元素表示该位置是否被访问过。当一个元素被访问时，将 [NC]38. 螺旋矩阵/顺时针打印数组 - 图6 中的对应位置的元素设为已访问。
如何判断路径是否结束？
由于矩阵中的每个元素都被访问一次，因此路径的长度即为矩阵中的元素数量，当路径的长度达到矩阵中的元素数量时即为完整路径，将该路径返回。

复杂度分析

时间复杂度： [NC]38. 螺旋矩阵/顺时针打印数组 - 图7 ，其中[NC]38. 螺旋矩阵/顺时针打印数组 - 图8 和[NC]38. 螺旋矩阵/顺时针打印数组 - 图9 分别是输入矩阵的行数和列数。

  1.   - 矩阵中的每个元素都要被访问一次。

空间复杂度：[NC]38. 螺旋矩阵/顺时针打印数组 - 图10 

  1.   - 需要创建一个大小为![](https://cdn.nlark.com/yuque/__latex/77cf678875ddf95e222fbb5de5c483a9.svg#card=math&code=m%C3%97n&id=WiVVH)的矩阵  ![](https://cdn.nlark.com/yuque/__latex/f3888f4df205089c381b4e6d0887210e.svg#card=math&code=%5Csmall%20%5Ctext%7Bvisited%7D&id=dS49N) 记录每个位置是否被访问过。

我的代码

  1. package array.array66;
  3. import java.util.ArrayList;
  4. import java.util.List;
  6. class Solution {
  7.     public List<Integer> spiralOrder(int[][] matrix) {
  8.         List<Integer> res = new ArrayList<Integer>();
  9.         //1. 检查非法越界
  10.         if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
  11.             return res;
  12.         }
  13.         //2. 记录行、列数
  14.         int rows = matrix.length, columns = matrix[0].length;
  15.         //3. 创建标记数组
  16.         boolean[][] visited = new boolean[rows][columns];
  17.         //4. 总数量
  18.         int total = rows * columns;
  19.         //5. 左上角起始点(0,0)
  20.         int row = 0, column = 0;
  21.         //6. 方向数组
  22.         int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
  23.         int directionIndex = 0;
  24.         for (int i = 0; i < total; i++) {
  25.             res.add(matrix[row][column]);   //集合添加当前元素
  26.             visited[row][column] = true;    //当前元素标记访问
  27.             int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
  28.             //7. 新坐标越界或者当前坐标已被标记访问，转入下一个方向
  29.             if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {
  30.                 directionIndex = (directionIndex + 1) % 4;
  31.             }
  32.             row += directions[directionIndex][0];
  33.             column += directions[directionIndex][1];
  34.         }
  35.         return res;
  36.     }
  37. }

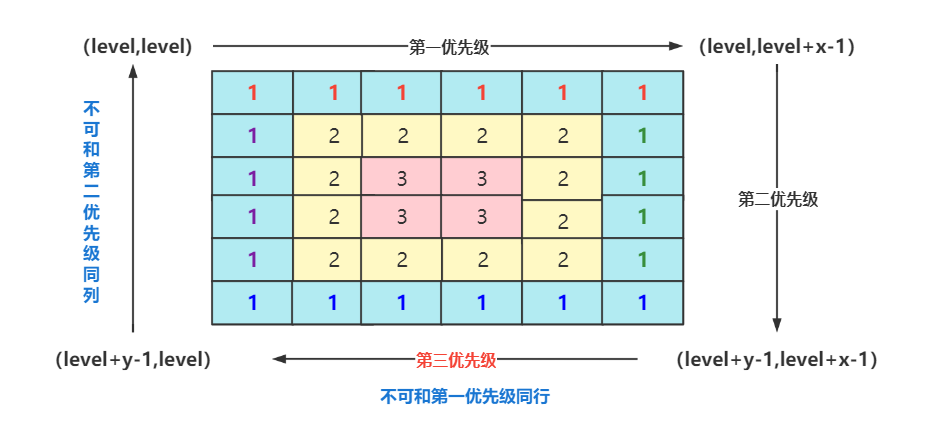
解题思路：按层模拟

脱衣服一样，一层层脱
可以将矩阵看成若干层，首先输出最外层的元素，其次输出次外层的元素，直到输出最内层的元素。

对于每层，从左上方开始以顺时针的顺序遍历所有元素。假设当前层的左上角位于 [NC]38. 螺旋矩阵/顺时针打印数组 - 图11，右下角位于 [NC]38. 螺旋矩阵/顺时针打印数组 - 图12 ，按照如下顺序遍历当前层的元素。

  1.   - _从左到右遍历上侧元素，依次为 _![](https://cdn.nlark.com/yuque/__latex/3d5368bdd8ce4de96c5e50617c5a5b9c.svg#card=math&code=%5Ctext%7B%28level%2Clevel%29%7D&id=zKPas)_ 到_![](https://cdn.nlark.com/yuque/__latex/45e3304b47f5962d7d84d70401fbe473.svg#card=math&code=%5Ctext%7B%28level%2Clevel%2Bx-1%29%7D&id=wjPoL)_ 。_
  2.   - _从上到下遍历右侧元素，依次为_![](https://cdn.nlark.com/yuque/__latex/ce3a571c02a2cbff0eec4cbf0e0108bc.svg#card=math&code=%5Ctext%7B%28level%2B1%2Clevel%2Bx-1%29%7D&id=UPUsl)_到 _![](https://cdn.nlark.com/yuque/__latex/cd9150e6f33528236ae8b7d1e7bf8d90.svg#card=math&code=%5Ctext%7B%28level%2By-1%2Clevel%2Bx-1%29%7D&id=qFVXY)_。_
  3.   - _从右到左遍历下侧元素，依次为_![](https://cdn.nlark.com/yuque/__latex/cd9150e6f33528236ae8b7d1e7bf8d90.svg#card=math&code=%5Ctext%7B%28level%2By-1%2Clevel%2Bx-1%29%7D&id=mgQgk)_到 _![](https://cdn.nlark.com/yuque/__latex/b9ca38f046dcee3351e6259d3e461d12.svg#card=math&code=%5Ctext%7B%28level%2By-1%2Clevel%29%7D&id=nmixH)_ _

不能与 step1 同行。

  1.   - _从下到上遍历左侧元素，依次为_![](https://cdn.nlark.com/yuque/__latex/23d4086c27ff18c7dadf58826b177ea2.svg#card=math&code=%5Ctext%7B%28level%2By-2%2Clevel%29%7D&id=nD0si)_到 _![](https://cdn.nlark.com/yuque/__latex/b1a3e228e42c123c7c8ff0b71b0d680a.svg#card=math&code=%5Ctext%7B%28level%2B1%2Clevel%29%7D&id=Zdw2s)

不能与 step2 同列。

遍历完当前层的元素后，将 [NC]38. 螺旋矩阵/顺时针打印数组 - 图13 增加 [NC]38. 螺旋矩阵/顺时针打印数组 - 图14，将 [NC]38. 螺旋矩阵/顺时针打印数组 - 图15 和 [NC]38. 螺旋矩阵/顺时针打印数组 - 图16 分别减少 [NC]38. 螺旋矩阵/顺时针打印数组 - 图17，进入下一层继续遍历，直到遍历完所有元素。
image.png

复杂度分析

时间复杂度： [NC]38. 螺旋矩阵/顺时针打印数组 - 图19 ，其中 m 和 n 分别是输入矩阵的行数和列数。

  1.   - 矩阵中的每个元素都要被访问一次。

空间复杂度：[NC]38. 螺旋矩阵/顺时针打印数组 - 图20 ，除了输出数组以外，空间复杂度是常数。

我的代码

  1. public class Solution {
  2.     public  ArrayList<Integer> travlaMatrix(int[][] matrix, int level, int x, int y){    //x坐标长度,纵坐标长度
  3.         ArrayList<Integer> res=new ArrayList<>();
  4.         while(x>0&&y>0){
  5.             for(int i=0;i<x;i++)
  6.                 res.add(matrix[level][level+i]);
  7.             for(int i=1;i<y-1;i++)
  8.                 res.add(matrix[level+i][level+x-1]);
  9.             for(int i=x-1;i>=0&&y-1>0;i--)  //不能和第1个for同行
  10.                 res.add(matrix[level+y-1][level+i]);
  11.             for(int i=y-2;i>0&&x-1>0;i--)   //不能和第2个for同列
  12.                 res.add(matrix[level+i][level]);
  13.             level++;x-=2;y-=2;
  14.         }
  15.         return res;
  16.     }
  18.     public  ArrayList<Integer> spiralOrder(int[][] matrix) {
  19.         ArrayList<Integer> res=new ArrayList<>();
  20.         if(matrix.length==0)return res;
  21.         res=travlaMatrix(matrix,0,matrix[0].length,matrix.length);
  22.         return res;
  23.     }
  24. }