[LeetCode]Ar605. 种花问题

🚩传送门：https://leetcode-cn.com/problems/can-place-flowers/

题目

假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false。

示例 1：

输入：flowerbed = [1,0,0,0,1], n = 1 输出：true

示例 2：

输入：flowerbed = [1,0,0,0,1], n = 2 输出：false

解题思路：贪心

判断能否在不打破种植规则的情况下在花坛内种入 n 朵花，从贪心的角度考虑，应该在不打破种植规则的情况下种入尽可能多的花，然后判断可以种入的花的最多数量是否大于或等于 n。
不难发现种花规则：

1. 当 _p_ 是奇数时最多可以在该范围内种植 朵花
2. 当 _p_ 是偶数时最多可以在该范围内种植 朵花。

由于 p 是偶数时，在整数除法的规则下 和 相等，因此无论奇数还是偶数，都是最多可种朵花
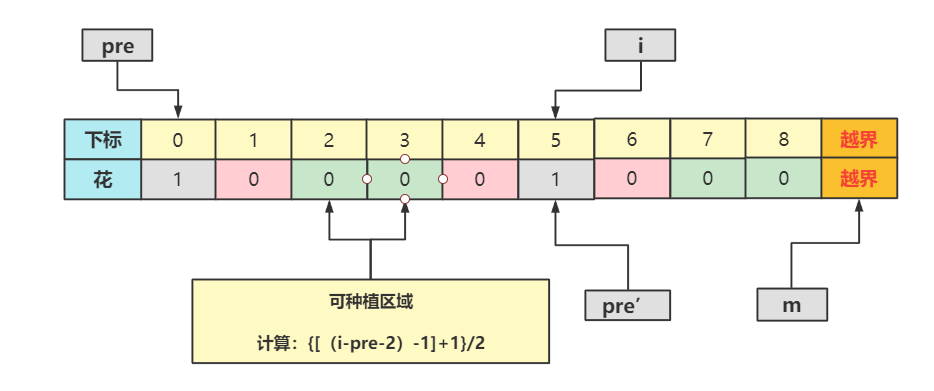
计算具体做法如下：

1. 维护 表示上一朵已经种植的花的下标位置，初始时 ，表示尚未遇到任何已经种植的花。
2. 从左往右遍历数组 ，当遇到 时根据 和 的值计算上一个区间内可以种植花的最多数量，然后令 ，继续遍历数组 剩下的元素。
3. 遍历数组 结束，根据数组 和长度 的值计算最后一个区间内可以种植花的最多数量。
4. 判断整个花坛内可以种入的花的最多数量是否大于或等于。

复杂度分析

时间复杂度：，其中 是数组 的长度 ，需要遍历数组一次。

空间复杂度： ，额外使用的空间为常数。

官方代码

class Solution {
    public boolean canPlaceFlowers(int[] flowerbed, int n) {
        int count = 0;
        int m = flowerbed.length;
        int prev = -1;
        for (int i = 0; i < m; i++) {
            if (flowerbed[i] == 1) {
                //1.遇到的第一个花
                if (prev < 0) 
                    count += i / 2;
                //2.和pre花朵的坐标进行计算
                else 
                    count += (i - prev - 2) / 2;
                //3.当前花朵标记为pre花朵
                prev = i;
            }
        }
        //处理最后一个花朵与花坛边界的空间
        if (prev < 0) {
            count += (m + 1) / 2;
        } else {
            count += (m - prev - 1) / 2;
        }
        return count >= n;
    }
}

由于只需要判断能否在不打破种植规则的情况下在花坛内种入 n 朵花，不需要具体知道最多可以在花坛内种入多少朵花，因此可以在循环内进行优化，当可以种入的花的数量已经达到 n，则可以直接返回 true，不需要继续计算数组剩下的部分。

优化代码

class Solution {
    public boolean canPlaceFlowers(int[] flowerbed, int n) {
        int count = 0;
        int m = flowerbed.length;
        int prev = -1;
        for (int i = 0; i < m; i++) {
            if (flowerbed[i] == 1) {
                //1.遇到的第一个花
                if (prev < 0) {
                    count += i / 2;
                }
                //2.和pre花朵的坐标进行计算
                else {
                    count += (i - prev - 2) / 2;
                }
                //3.判断是否终止计算
                if (count >= n) {
                    return true;
                }
                prev = i;
            }
        }
        if (prev < 0) {
            count += (m + 1) / 2;
        } else {
            count += (m - prev - 1) / 2;
        }
        return count >= n;
    }
}