题1：二叉树中和为某一值的路径 II

判断二叉树中是否包含和为某一值的路径

题目来源：[NC]9. 二叉树中和为某一值的路径(一)
[LC]112. 二叉树中和为某一值的路径(一)

题目

给定一个二叉树 root和一个值 sum ，判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。

示例 1：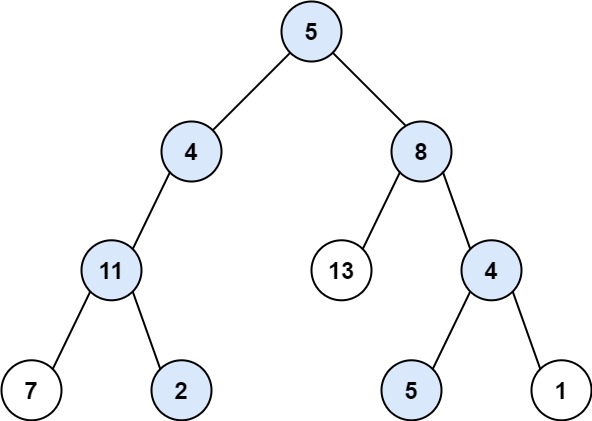
🍗二叉树中和为某一值的路径合集 - 图1

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出：true

思路：递归

如果当前结点非空，则递归左右子树，递归时将 **sum-=root.val** ，当遇到叶子节点时候，如果 sum==0 说明存在 此路径 。

时间复杂度：🍗二叉树中和为某一值的路径合集 - 图2，其中 🍗二叉树中和为某一值的路径合集 - 图3 为二叉树的节点个数。即遍历一棵二叉树的时间复杂度，每个结点只被访问一次。

空间复杂度：🍗二叉树中和为某一值的路径合集 - 图4，其中 🍗二叉树中和为某一值的路径合集 - 图5 是二叉树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为🍗二叉树中和为某一值的路径合集 - 图6。平均情况下树的高度与节点数的对数正相关，空间复杂度为 🍗二叉树中和为某一值的路径合集 - 图7。

🚩我的代码

  1. public class Solution {
  3.     public boolean hasPathSum (TreeNode root, int sum) {
  4.         if (root == null) {
  5.             return false;
  6.         }
  7.         sum -= root.val;
  8.         if (root.left == null && root.right == null && sum == 0) {
  9.             return true;
  10.         }
  11.         boolean left=hasPathSum(root.left, sum);
  12.         boolean right=hasPathSum(root.right, sum);
  13.         return left||right;
  14.     }
  15. }

题2：二叉树中和为某一值的路径 II

打印出二叉树中和为某一值的所有路径

题目来源：[NC]8. 二叉树中和为某一值的路径(二)
[LC]剑指34. 二叉树中和为某一值的路径(二)
[LC]剑指113. 二叉树中和为某一值的路径(二)

题目

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点 路径总和 等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：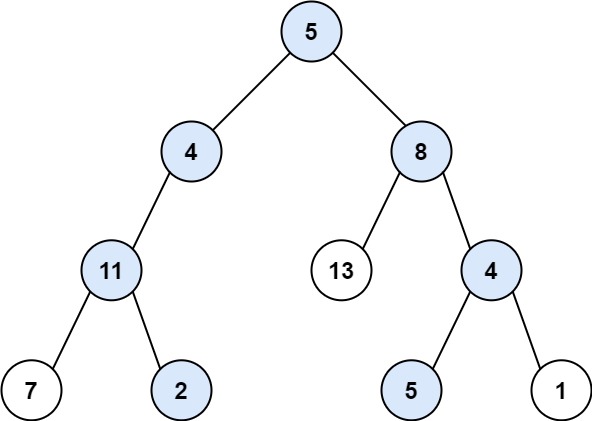
🍗二叉树中和为某一值的路径合集 - 图8

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出：[[5,4,11,2],[5,8,4,5]]

示例 2：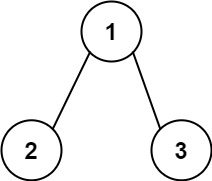
🍗二叉树中和为某一值的路径合集 - 图9

输入：root = [1,2,3], targetSum = 5 输出：[]

思路：递归

首先用临时 list 记录走下的路径结点，遇到叶子结点时，若临时 list 中的和等于 sum ，则将 list 数据加入 ans
算法流程：

  1. 当前结点非空则用 list 保存 结点值
  2. 然后递归左子树
  3. 接着递归右子树
  4. 若遇到叶子结点时，若临时 list 中的和等于 sum ，则将 list 数据加入 ans

递归完成，则所有符合条件的答案存入 ans

时间复杂度：🍗二叉树中和为某一值的路径合集 - 图10，其中 🍗二叉树中和为某一值的路径合集 - 图11 是树的节点数，在最坏情况下，树的上半部分为链状，下半部分为完全二叉树，并且从根节点到每一个叶子节点的路径都符合题目要求。此时，路径的数目为 🍗二叉树中和为某一值的路径合集 - 图12，并且每一条路径的节点个数也为 🍗二叉树中和为某一值的路径合集 - 图13，因此要将这些路径全部添加进答案中，时间复杂度为🍗二叉树中和为某一值的路径合集 - 图14。

空间复杂度： 🍗二叉树中和为某一值的路径合集 - 图15，其中 🍗二叉树中和为某一值的路径合集 - 图16 是树的节点数 ，空间复杂度主要取决于栈空间的开销，栈中的元素个数不会超过树的节点数。

🚩官方代码

  1. class Solution {
  2.     LinkedList<List<Integer>> res = new LinkedList<>();
  3.     LinkedList<Integer> path = new LinkedList<>(); 
  4.     public List<List<Integer>> pathSum(TreeNode root, int sum) {
  5.         dfs(root, sum);
  6.         return res;
  7.     }
  8.     void dfs(TreeNode root, int tar) {
  9.         if(root == null) return;
  10.         path.add(root.val);
  11.         tar -= root.val;
  12.         if(tar == 0 && root.left == null && root.right == null)
  13.             res.add(new LinkedList(path));
  14.         dfs(root.left, tar);
  15.         dfs(root.right, tar);
  16.         path.removeLast();
  17.     }
  18. }

题3：二叉树中和为某一值的路径 III

题目来源：[NC]162. 二叉树中和为某一值的路径(三)
[LC] 437. 二叉树中和为某一值的路径(三)

题目

给定一个二叉树的根节点 root，和一个整数 targetSum，求该二叉树里节点值之和等于 targetSum的 路径 的数目。每个二叉树的节点值可正可负 。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的 。

只能从父节点到子节点

示例 1：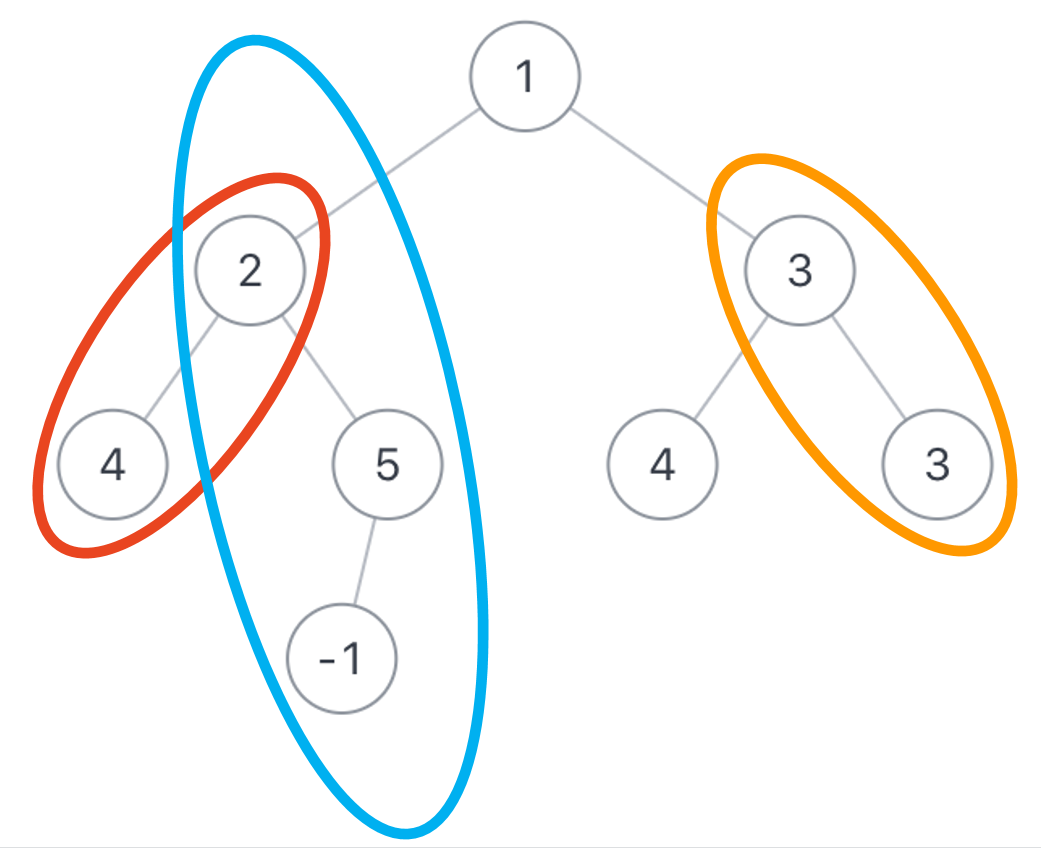
🍗二叉树中和为某一值的路径合集 - 图17

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出：3 解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出：3

思路：递归

穷举所有的可能，我们访问每一个节点 🍗二叉树中和为某一值的路径合集 - 图18，检测以 🍗二叉树中和为某一值的路径合集 - 图19 为起始节点且向下延深的路径有多少种。然后我们再递归遍历树中的每一个节点为起始结点的所有可能的路径，然后将这些路径数目加起来即为返回结果。

时间复杂度：🍗二叉树中和为某一值的路径合集 - 图20，其中 🍗二叉树中和为某一值的路径合集 - 图21 是树的节点数，对于每一个节点，求以该节点为起点的路径数目时，则需要遍历以该节点为根节点的子树的所有节点，因此求该路径所花费的最大时间为 🍗二叉树中和为某一值的路径合集 - 图22，我们会对每个节点都求一次以该节点为起点的路径数目，因此时间复杂度为🍗二叉树中和为某一值的路径合集 - 图23。

空间复杂度： 🍗二叉树中和为某一值的路径合集 - 图24，考虑到递归需要在栈上开辟空间。

🚩官方代码

  1. class Solution {
  2.     public int pathSum(TreeNode root, int targetSum) {
  3.         if (root == null) return 0;                // 1. 当前结点空,返回 0
  4.         int ret = rootSum(root, targetSum);        // 2. 统计当前结点作为起始点的路径个数
  5.         ret += pathSum(root.left, targetSum);    // 3. 递归统计左子树作为起始点的路径个数
  6.         ret += pathSum(root.right, targetSum);    // 4. 递归统计右子树作为起始点的路径个数
  7.         return ret;                                // 5. 返回总的答案
  8.     }
  10.     // 计算当前root作为起始点的路径个数
  11.     public int rootSum(TreeNode root, int targetSum) {
  12.         int ret = 0;
  13.         if (root == null) {
  14.             return 0;
  15.         }
  16.         if (root.val == targetSum) {
  17.             ret++;
  18.         } 
  19.         ret += rootSum(root.left,  targetSum - root.val);
  20.         ret += rootSum(root.right, targetSum - root.val);
  21.         return ret;
  22.     }
  23. }

🐛思路：前缀和

前缀和定义：一个节点的前缀和就是该节点到根之间的路径和。
举例子说明：二叉树及对应结点的前缀和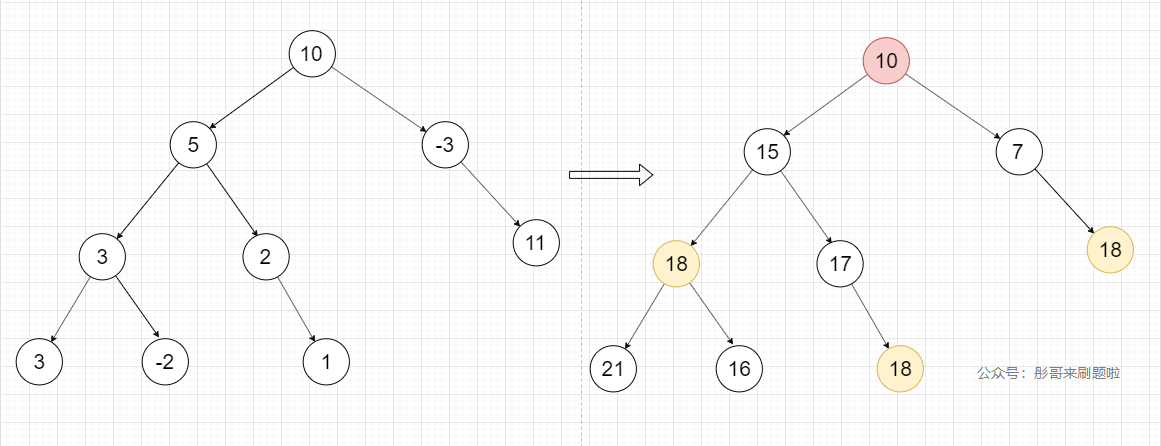
🍗二叉树中和为某一值的路径合集 - 图25

节点5 的前缀和：10 + 5 = 15
节点3 的前缀和：10 + 5 + 3 = 18
节点-2的前缀和：10 + 5 + 3 + （-2） = 16

前缀和对于本题的作用：两节点间的路径和 = 两节点的前缀和之差
还是拿下图解释：

  1.                        1
  2.                     / 
  3.                    2    
  4.                   / 
  5.                  3   
  6.                 / 
  7.                4

假如题目给定数值为5

  1. 节点1的前缀和为: 1
  2. 节点3的前缀和为: 1 + 2 + 3 = 6
  4. prefix(3) - prefix(1) == 5
  5. # 所以【节点1】到【节点3】之间有一条符合要求的路径( 2 --> 3 )

理解了这个之后，问题就得以简化，我们只用遍历整颗树一次，记录每个节点的前缀和，并查询该节点的祖先节点中符合条件的个数，将这个数量加到最终结果上。

🚩HashMap 的 key 是前缀和， value 是该前缀和的节点数量，记录数量是因为有出现复数路径的可能。
拿图说明：

  1.       1    (#0:prefix:1)
  2.      / 
  3.     0 (#1:prefix:1)
  4.    /
  5.   2 (#2:prefix:3)    
  7. # prefix:3 - # prefix:1 = 2

上图前缀和为1的节点有(1)、(0)，故路径和为2的路径数也有两条，(0->2)、(2)

恢复状态的意义： 在遍历完当前节点的所有子节点后，将当前结点从 map 信息中除去 。
由于题目要求：路径方向必须是向下的（只能从父节点到子节点）
当我们讨论两个节点的前缀和差值时，有一个前提：一个节点必须是另一个节点的祖先节点

换句话说，当我们把一个节点的前缀和信息更新到map里时，它应当只对其子节点们有效。

举个例子，下图中有两个值为2的节点（A, B)。

  1.       0
  2.      /  \
  3.     A:2  B:2
  4.    / \    \
  5.   4   5    6
  6.  / \   \
  7. 7   8   9

当我们遍历到最右方的节点6时，对于它来说，此时的前缀和为2的节点只该有B, A并不是节点6的祖先节点。

如果我们不做状态恢复，当遍历右子树时，左子树中A的信息仍会保留在 map 中，那此时节点6就会认为A, B都是可追溯到的节点，从而产生错误。

状态恢复代码的作用就是： 在遍历完当前节点的所有子节点后，将当前结点从 map 信息中除去 。

时间复杂度：🍗二叉树中和为某一值的路径合集 - 图26，其中 🍗二叉树中和为某一值的路径合集 - 图27 为二叉树中节点的个数。利用前缀和只需遍历一次二叉树即可。

空间复杂度： 🍗二叉树中和为某一值的路径合集 - 图28，考虑到递归需要在栈上开辟空间。

🐛 官方代码

  1. class Solution {
  2.     public int pathSum(TreeNode root, int sum) {
  3.         // key 是前缀和, value 是大小为 key 的前缀和出现的次数
  4.         Map<Integer, Integer> prefixSumCount = new HashMap<>();
  5.         // 前缀和为 0 的一条路径
  6.         prefixSumCount.put(0, 1);
  7.         return recursionPathSum(root, prefixSumCount, sum, 0);
  8.     }
  10.     private int recursionPathSum(TreeNode node, Map<Integer, Integer> prefixSumCount, int target, int currSum) {
  11.         // 1. 递归终止条件
  12.         if (node == null) return 0;  
  13.         // 2. 统计当前结点做路径和末尾结点,可以得到的路径个数
  14.         int res = 0;
  15.         // 3. 计算当前结点的前缀和
  16.         currSum += node.val;
  17.         // 4. 计算路径和个数
  18.         res += prefixSumCount.getOrDefault(currSum - target, 0);
  19.         // 5. 更新路径上前缀和为 currSum 的个数
  20.         prefixSumCount.put(currSum, prefixSumCount.getOrDefault(currSum, 0) + 1);
  21.         // 6. 递归左右子结点
  22.         res += recursionPathSum(node.left, prefixSumCount, target, currSum);
  23.         res += recursionPathSum(node.right, prefixSumCount, target, currSum);
  24.         // 7. 当前节点的所有子节点遍历完后,当前结点信息失去效应应当移除
  25.         prefixSumCount.put(currSum, prefixSumCount.get(currSum) - 1);
  26.         return res;
  27.     }
  28. }

注意：为什么计算计算路径和个数使用 currSum - target ？

答：currSum-target相当于找路径的起点，起点的sum+target=curSum，当前点到起点的距离就是target