[NC]279. 二叉树的下一个结点/二叉搜索树中的中序后继

🚩传送门：牛客题目
力扣题目

题目

给定一棵二叉搜索树和其中的一个节点 ，找到该节点在树中的中序后继。如果节点没有中序后继，请返回 。

节点 的后继是中序遍历的顺序节点 的下一个节点。

示例 1：

输入：root = [2,1,3], p = 1 输出：2 解释：这里 1 的中序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。

示例 2：

输入：root = [5,3,6,2,4,null,null,1], p = 6 输出：null 解释：因为给出的节点没有中序后继，所以答案就返回 null 了。

解题思路：牛客

在牛客题目中，树中的结点不仅包含左右子结点，同时包含指向父结点的next指针，函数的形参只给出节点 ，而没有根结点 。

因此对于 我们只需要考虑以下两种情况：

1. 节点 有右孩子即
2. 节点 无右孩子即

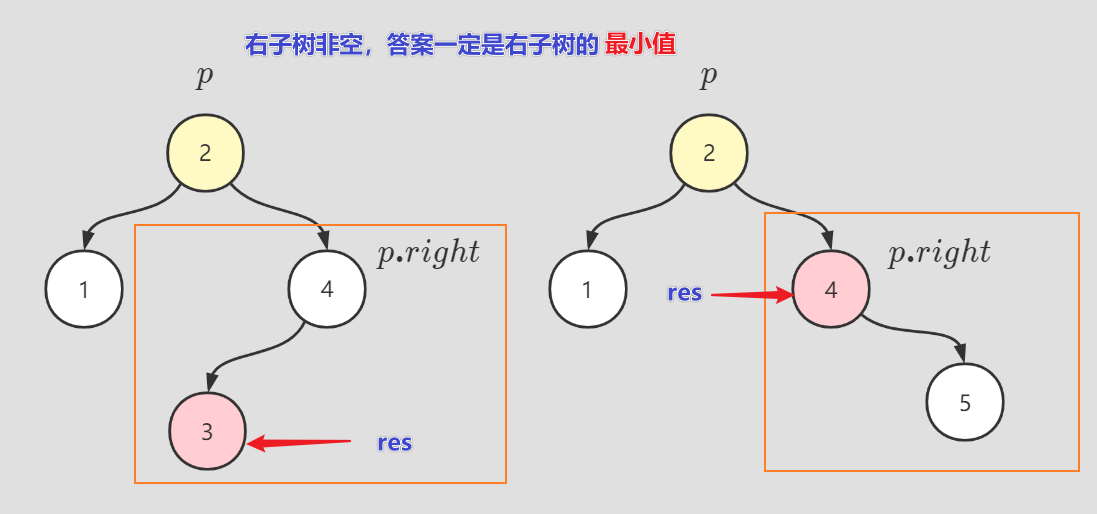
节点 有右孩子情形：

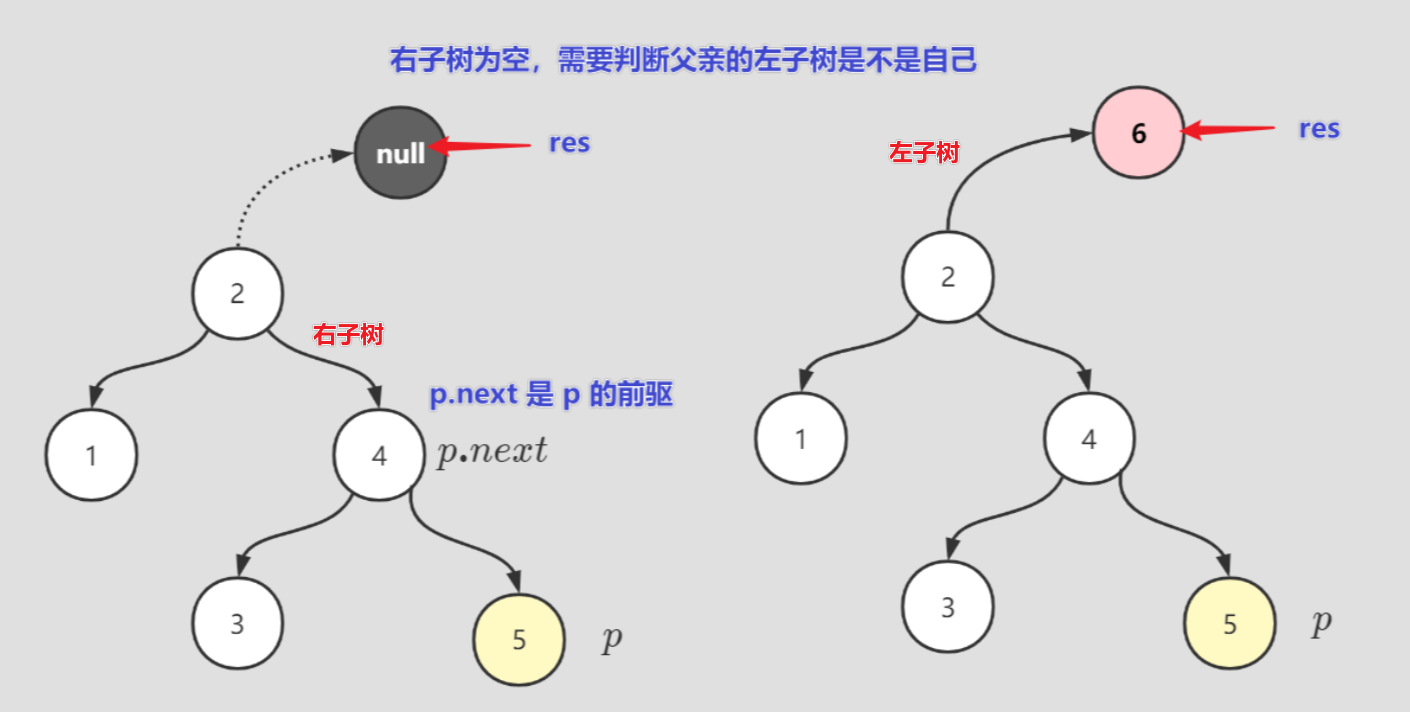
节点 无右孩子情形：

需要考虑 是父亲 的左子树还是右子树

• 是父亲 的左子树，父亲 就是自己的下一个序列
• 是父亲 的右子树，父亲 就是自己的上一个序列，此时继续上述检查，直至

我的代码

public class Solution {
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
        // 如果有右子树,下一个序列一定在右子树
        // 在右子树中查找最小值
        if (pNode.right != null) {
            pNode = pNode.right;
            // 最小值一定是最左结点
            while (pNode.left != null) {
                pNode = pNode.left;
            }
            return pNode;
        }
        // 右子树是空的,判断自己是父亲的左子树还是右子树
        // 自己是父亲的左子树,父亲就是自己的下一个序列
        // 自己是父亲的右子树,父亲就是自己的上一个序列,此时需要继续向上寻找,直至pNode.next == null
        while (pNode.next != null) {
            // pNode是父亲的左子树,父亲就是自己的下一个序列
            if (pNode.next.left == pNode)
                return pNode.next;
            pNode = pNode.next;
        }
        return null;
    }
}

解题思路：力扣

在力扣题目中，树中的结点仅包含左右子结点，函数的形参不光给出节点 ，还给出根结点 。

我们知道中序遍历的规则：是由小到大有序的，比大的值一定后遍历

我们只要从根节点二叉树搜索一定能找到第一个大于 的结点 ，结点一定是的后面遍历结点，但具体是不是后继不知道

那么 ，即当前被标记为是后遍历的结点，只需 去 的左子树看看，因为比 先遍历的定在 的左子树。

• 如果左子树中出现了 则说明此时是后遍历的结点，且比标记的早，因此刷新 。

• 如果左子树中 则去 的右子树看看

  class Solution {
    public TreeNode inorderSuccessor(TreeNode pRoot, TreeNode pNode) {
        TreeNode cur = pRoot;
        TreeNode result = null;
        while (cur!=null) {
            if (cur.val > pNode.val) {
                result = cur;
                cur = cur.left;
            } else {
                cur = cur.right;
            }
        }
        return result;
    }
  }