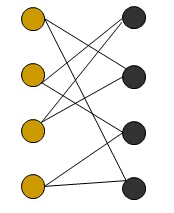
预备知识基本概念
二分图
定义
1. 二分图又称作**二部图**,是图论中的一种特殊模型 。1. 若能将无向图 **G=(V,E)** 的顶点 **V** 划分为两个交集为空的顶点集,并且**任意边**的两个**端点都分属于两个集合**,则称图G为一个为二分图 。- **解释:****V**所有**顶点集合,E**所有**边集合**
匹配
一个匹配即一个包含若干条边的集合,且其中任意两条边没有公共端点
- **解释:****匹配集合**就是**所有红边集合,**所有红边的端点不可能是冲突
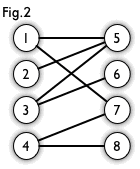 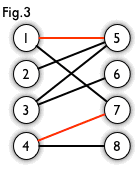
1.最大匹配
边数最大的子集称为图的最大匹配问题,最大匹配的边数称为最大匹配数
例如
假如你是月老,可以撮合任何一对有暧昧关系的男女,那么你最多能成全多少对情侣? 最大匹配问题
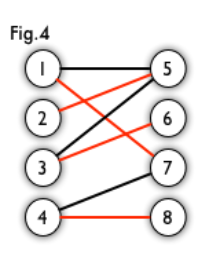<br /> 如图,图4即为**最大匹配图**和**完美匹配图**
2.完美匹配 / 完全匹配 / 最优匹配
完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突
备注:并非每个图都存在完美匹配
其实三个形容词都是指两个集内的所有顶点能够一一匹配,并且所获得的权值最大或最小
**最优匹配又称为带权最大匹配**,是指在带有权值边的二分图中,求一个匹配使得匹配边上的权 值和最大。一般X和Y集合顶点个数相同,最优匹配也是一个完备匹配,即每个顶点都被匹配。 如果个数不相等,可以通过补点加0边实现转化。一般使用KM算法解决该问题。
3.最小覆盖
二分图的最小覆盖分为最小顶点覆盖和最小路径覆盖
1. 最小顶点覆盖:
我们想找到最少的一些点,使二分图所有的边都至少有一个端点在这些点中
- **备注:**倒过来说就是,**删除包含这些点的边,可以删掉所有边**
- 二分图的最小顶点覆盖数 **= **二分图的最大匹配数**(****König定理****)**
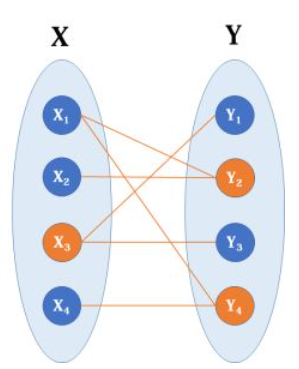
1. 最小路径覆盖也称为最小边覆盖:
用尽量少的不相交简单路径覆盖二分图中的所有顶点。
- 二分图的最小路径覆盖数 **= **|V|-二分图的最大匹配数
4.最大独立集
匈牙利算法基本概念
交替路
从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边……形成的路径叫交替路。
增广路
从一个未匹配的点出发,走交替路,到达了一个未匹配过的点,这条路叫做增广路
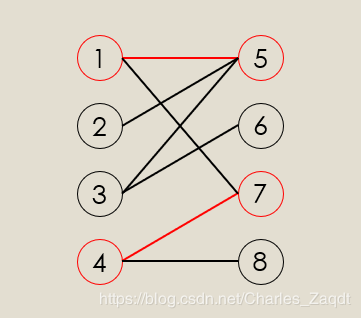<br />**例子**<br />看图,其中**1、4、5、7****是已经匹配的点**,**1->5 , 4->7是已经匹配的边**<br />那么我们从8开始出发,**8->4->7->1->5->2 **这条交替路就是一条**增广路**
匈牙利算法的流程
一.简单理解
现在我们来看看匈牙利算法是怎么运作的
原则 :**先到先得,能让则让 [ 还能找到女朋有的前提下 ]**
我们从B1看起( 男女平等,从女生这边看起也是可以的 ),他与G2有暧昧,那我们就先暂时把他与G2连接
备注:这时只是暂时构想,没有真正安排
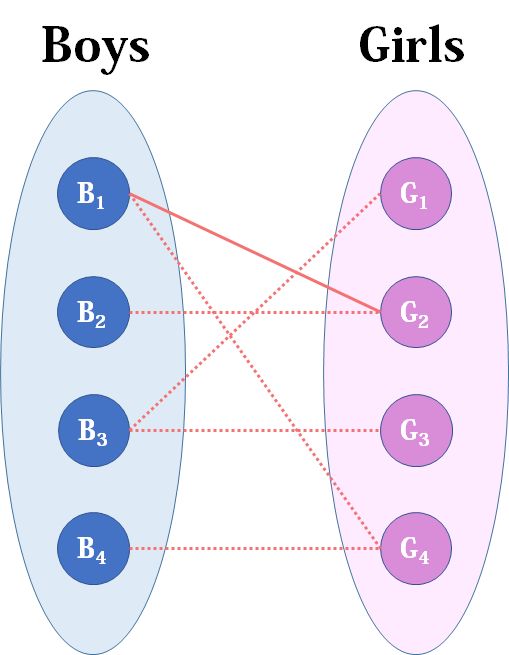
来看B2,B2也喜欢G2,这时G2已经” 名花有主 “了,我们回溯回去看G2目前被安排的男友B1
B1能不能换个对象呢?可以换 G4,且 G4 还没有被安排,那我们就让 B1 换成上 G4
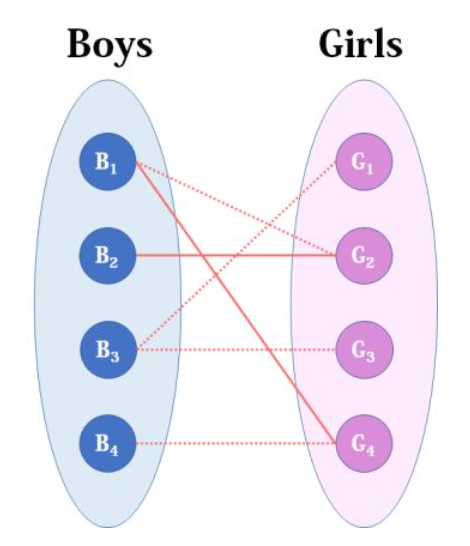
然后B3,B3直接配上G1就好了,这没什么问题。
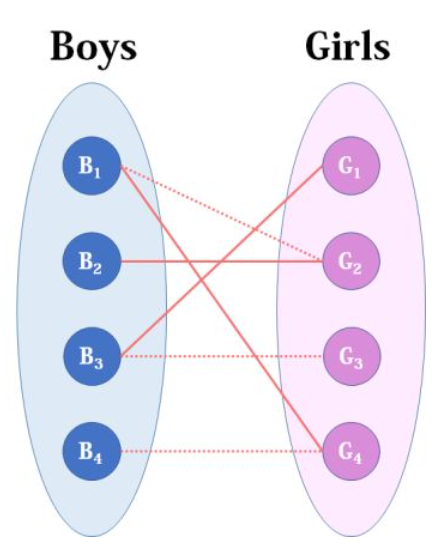[ 将描述**整个递归过程** ]
至于**B4**,他喜欢 G4,这时G4已经" **名花有主** "了,**B4** 跑过去问** B1** 你能不能换对象?把G4 让给我 B4
[ B4询问B1]
- B1 不知道能不能让对象,跑回去看了看自己的女生备胎,有个G2,但是G2有了男朋友 B2
B1 跑过去问 B2,你能不能换对象?把G2 让给我 [ 本着好心人,有备胎的话能让就让 **]**
[ B1询问B2]B2 也不知道能不能让对象,也跑回去看了看自己的女生备胎,没备胎
对B1 说不行,不能让,让了没对象了 [ 事关自己性福,**不能让 ]**
- B1 遍历女生备胎,只发现了 G2 ,别人不让给他,所以他也不**能让**,让了他也没女朋友了
最终B4没有女朋友
<br />** 最终最大匹配结果图 **<br />**上述示例的验证代码**# include<iostream> using namespace std; #define maxM 5 #define maxN 5 int M, N; //M, N分别表示左、右侧集合的元素数量 int Map[maxM][maxN] = { {0,0,0,0,0}, {0,0,1,0,1}, {0,0,1,0,0}, {0,1,0,1,0}, {0,0,0,0,1}, }; //邻接矩阵存图 int p[maxN]; //记录当前右侧元素所对应的左侧元素 bool vis[maxN]; //记录右侧元素是否已被访问过 bool match(int i) { for (int j = 1; j <= N; ++j) if (Map[i][j] && !vis[j]) {//有边且未访问 vis[j] = true; //记录状态为访问过 if (p[j] == 0 || match(p[j])) { //如果右侧暂无匹配,或者原来匹配的左侧元素可以找到新的匹配 p[j] = i; //当前左侧元素成为当前右侧元素的新匹配 return true; //返回匹配成功 } } return false; //循环结束,仍未找到匹配,返回匹配失败 } int Hungarian() { int cnt = 0; for (int i = 1; i <= M; ++i) { memset(vis, 0, sizeof(vis)); //重置vis数组 if (match(i)) cnt++; } return cnt; } int main(void) { M = N = 4; cout << Hungarian() << endl; return 0; }二.深入理解
由增广路的性质,增广路中的匹配边总是比未匹配边多一条,所以如果我们放弃一条增广路中的匹配边,选取未匹配边作为匹配边,则匹配的数量就会增加。
匈牙利算法就是在不断寻找增广路,如果找不到增广路,就说明达到了最大匹配。
例子
1、起始没有匹配 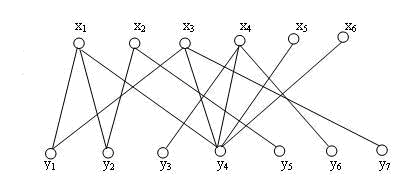
2、选中第一个 x1 点找第一个 y1 点连线 **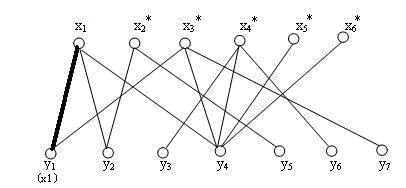
3、选中第二个 x2 点找第二个 y2 点连线 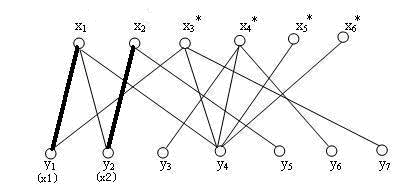
4、选中第三个 x3 点,发现 x3 的第一条边 x3 - y1 已经被人占了
- 解决措施:
- 找出 x3 出发的的交错路径 **x3-y1-x1-y4**,把交错路中已在匹配上的边 **x1-y1从匹配中去掉**
- 将剩余的边x3-y1-x1-y4 **加到匹配中去 **
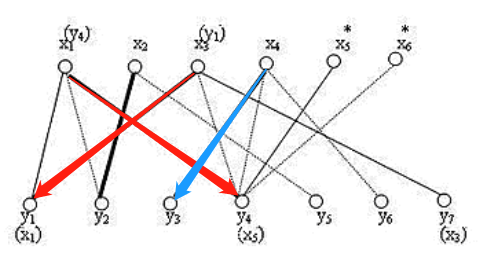
5、选中第四个 x4 点找第四个 y3 点连线
6、同理加入 x5 **,**x6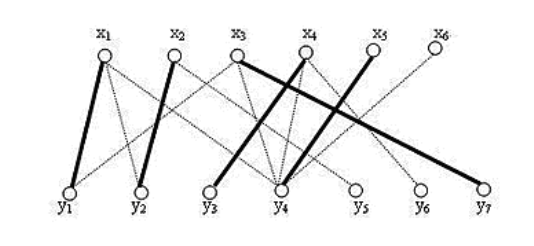
总结:
- 上述是针对的深度优先
- 匈牙利算法可以针对深度优先也可以针对广度优先
- 参数说明 :
- M变量 : 左集合的元素数量 ——-男朋友
- N变量 : 右集合的元素数量 ——-女朋友
- Map数组 : 邻接矩阵存图,存储路径关系
- p数组 : 记录当前右侧元素所对应的左侧元素—-存储女的男朋友
- vis数组 : 记录右侧元素是否已被访问过 —-存储女的有没有男朋友
*/
int M, N; //M, N分别表示左、右侧集合的元素数量
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN]; //记录当前右侧元素所对应的左侧元素
bool vis[MAXN]; //记录右侧元素是否已被访问过
bool match(int i){
for (int j = 1; j <= N; ++j)
if (Map[i][j] && !vis[j]) {//有边且未访问
} return false; //循环结束,仍未找到匹配,返回匹配失败 } int Hungarian(){ int cnt = 0; for (int i = 1; i <= M; ++i){ memset(vis, 0, sizeof(vis)); //重置vis数组 if (match(i))vis[j] = true; //记录状态为访问过 if (p[j] == 0 || match(p[j])){ //如果右侧暂无匹配,或者原来匹配的左侧元素可以找到新的匹配 p[j] = i; //当前左侧元素成为当前右侧元素的新匹配 return true; //返回匹配成功 }
} return cnt; } ```cnt++;