[LeetCode]77. 组合

🚩传送门：题目

题目

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 ：

输入：n = 4, k = 2 输出： [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

解题思路：递归实现组合型枚举

假设我们需要找到一个长度为 n 的序列 a 的所有子序列，代码框架是这样的：

void dfs(int cur, int n, int k) {
    if (cur > n + 1) return;  // Cur 增长的上界
    if (temp.size() == k) {
        //  ... 记录答案 ...
        return;
    }
    // 考虑选择当前位置
    temp.addLast(cur);        // List<Integer> temp = new LinekedList<>();
    dfs(cur + 1, n, k);
    temp.pollLast();
    // 考虑不选择当前位置
    dfs(cur + 1, n, k);
}

原序列每个位置在临时序列的状态有被选中和不被选中两种，我们用 temp 数组存放已经被选出的数字。

可以做一个剪枝，如果当前 temp 的大小为 s，未确定状态的区间 [cur,n] 的长度为 t，若 s + t < k，那么即使 t 个都被选中，也不可能构造出一个长度为 k 的序列，故这种情况就没有必要继续向下递归，即我们可以在每次递归开始的时候做一次这样的判断：

if (temp.size() + (n - cur + 1) < k) {
    return;
}

复杂度分析

时间复杂度：，其中 为长度 。

空间复杂度： ，即递归使用栈空间的空间代价和临时数组 temp 的空间代价。

栈空间需要递归 **n** 层，开销很大

我的代码

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> combine(int n, int k) {
        dfs(1, n, k);
        return res;
    }

    private void dfs(int start, int end, int k) {
        if (k == 0) {
            res.add(new ArrayList<>(path));
            return;
        }
        // 剪枝:区间 (n - k + 1,n] 不可能构造出一个长度为 k 的序列
        for (int i = start; i <= end - k + 1; i++) {
            path.add(i);
            dfs(i + 1, end, k - 1);
            path.remove(path.size() - 1);
        }
    }
}

解题思路：非递归（字典序法）实现组合型枚举

把原序列中被选中的位置记为 1，不被选中的位置记为 0，对于每个方案都可以构造出一个二进制数。
我们先看一看 n = 5，k = 3 的例子：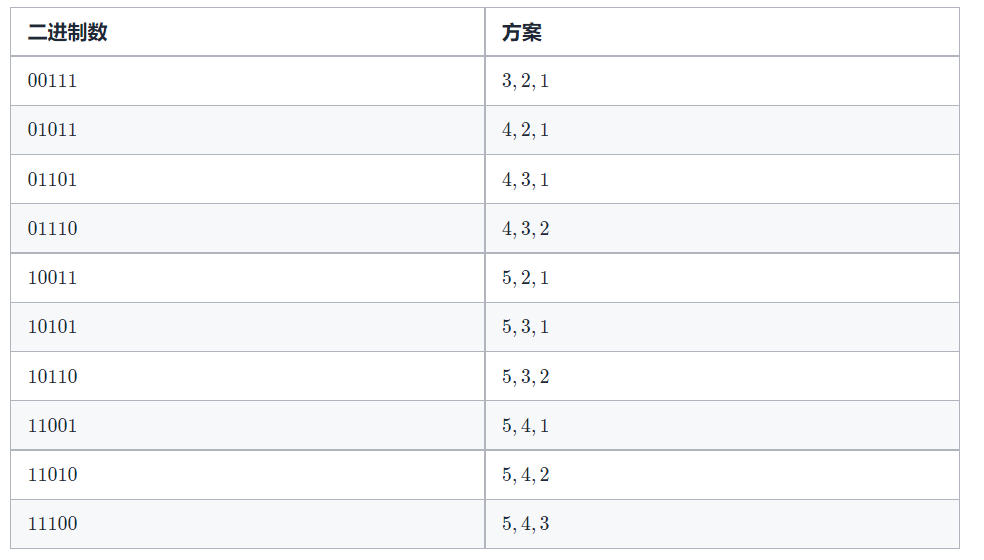

我们可以看出「对应的二进制数」一列包含了由 k 个 1 和 n - k 个 0 组成的所有二进制数，并且按照字典序排列。

这给了我们一些启发，我们可以通过某种方法枚举，使得生成的序列是根据字典序递增的。

nextpermutation（） 🤣 没错正是在下 ！

🚩 我们可以不断通过上述方案求 nextpermutation，就可以构造出所有的方案。完美！但是依旧可以优化

🍗 我们考虑不通过二进制数的字典序，而是如何直接在方案上变换来得到下一个方案呢 ？
算法流程：[ 参照上图和代码理解 ]
假设从低到高的 个数分别是 ，我们一定可以从低位向高位找到第一个位置 使得 ，我们知道出现在 序列中的数字在二进制数中对应的位置一定是 1，即表示被选中，那么 意味着 和 对应的二进制位中间有 0，即这两个 1 不连续。我们把 对应的 1 向高位推送，也就对应着 ，而对于 内所有的 把值恢复成 ，即对应这 个 1 被移动到了二进制数的最低 位。这似乎只考虑了上面的「规则二」。

但是实际上「规则一」是「规则二」在 **t=0** 时的特殊情况，因此这么做和按照两条规则模拟是等价的。

复杂度分析

时间复杂度：

  - 外层循环的执行次数是 ![](https://cdn.nlark.com/yuque/__latex/79333e3baaf02600326bd4bc6605d43c.svg#card=math&code=n%20%5Cchoose%20k&id=Cl8Xs)次，每次需要做一个 ![](https://cdn.nlark.com/yuque/__latex/18bfba88133de0dabea899170b5e687b.svg#card=math&code=O%28k%29%20&height=20&id=ZWuhK) 的添加答案和 ![](https://cdn.nlark.com/yuque/__latex/18bfba88133de0dabea899170b5e687b.svg#card=math&code=O%28k%29%20&height=20&id=OaNGH) 的内层循环 。

空间复杂度： ，即临时数组 temp 的空间代价。

我的代码

class Solution {
    List<Integer> temp = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

    public static List<List<Integer>> combine(int n, int k) {
        List<Integer> temp = new ArrayList<Integer>();
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        // 将 temp 中 [0, k - 1] 每个位置 i 设置为 i + 1，即 [0, k - 1] 存 [1, k]
        for (int i = 1; i <= k; ++i) {
            temp.add(i);
        }
        temp.add(n + 1);    // 末尾加一位 n + 1 作为哨兵

        int j = 0;
        while (j < k) {
            ans.add(new ArrayList<Integer>(temp.subList(0, k)));
            j = 0;
            // 1. 需要寻找第一个 temp[j] + 1 != temp[j + 1] 的位置 t
            // 2. 需要把 [0, t - 1] 区间内的每个位置重置成 [1, t]
            while (j < k && temp.get(j) + 1 == temp.get(j + 1)) {
                temp.set(j, j + 1);
                ++j;
            }
            // j 是第一个 temp[j] + 1 != temp[j + 1] 的位置
            temp.set(j, temp.get(j) + 1);
        }
        return ans;
    }
}