[LC]581. 最短无序连续子数组

🚩传送门：力扣题目

题目

给你一个整数数组 ，你需要找出一个 连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。
请你找出符合题意的 最短 子数组，并输出它的长度。

示例 1：

输入：nums = [2,6,4,8,10,9,15] 输出：5 解释：你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

解题思路：排序

我们可以假设把这个数组分成三段，左段和右段是标准的升序数组，中段数组虽是无序的，但满足最小值大于左段的最大值，最大值小于右段的最小值。

复杂度分析

时间复杂度：，其中 是给定数组的长度，我们需要排序该数组一次。

空间复杂度：,其中 是给定数组的长度，我们拷贝该数组一次。

官方代码

class Solution {
    public static int findUnsortedSubarray(int[] nums) {
        int[] sorted = Arrays.copyOfRange(nums, 0, nums.length);    // 拷贝新数组
        Arrays.sort(sorted);                                        // 新数组排序
        int i = 0, end = nums.length - 1;
        // 左段有序的,所以从左向右第一个不一致的下标就是中段的左边界begin
        while (begin < nums.length && sorted[begin] == nums[begin]) begin++; 
        while (end >= 0 && sorted[end] == nums[end]) end--;    // 右段有序的,所以从右向左第一个不一致的下标就是中段的右边界end
        return end <= begin ? 0 : end - begin + 1;            // 中段如果存在,begin必然小于end
    }
}

解题思路：一次遍历

我们可以假设把这个数组分成三段，左段和右段是标准的升序数组，中段数组虽是无序的，但满足最小值大于左段的最大值，最大值小于右段的最小值。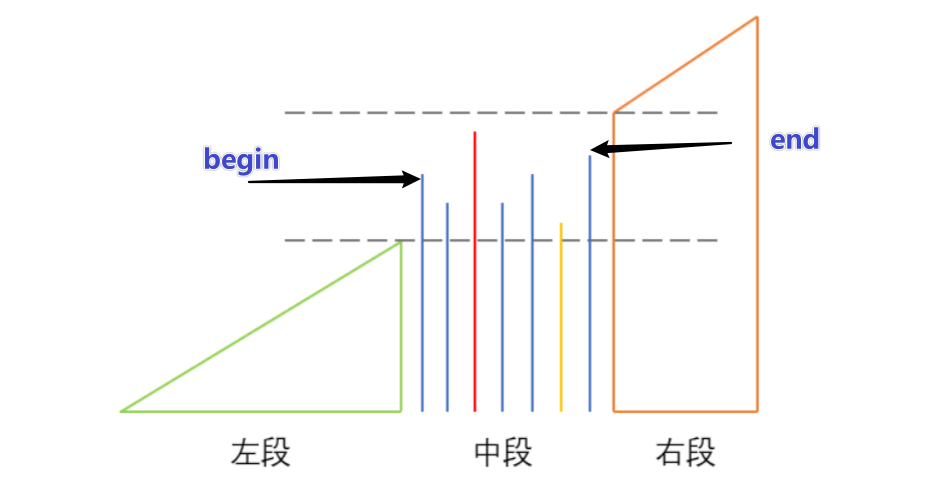

那么我们目标就很明确了，找中段的左右边界，我们分别定义为和 ;
分两头开始遍历：

• 从左到右维护一个最大值，在进入右段之前，遍历到的都是小于的，我们要求的是遍历中最后一个小于元素的位置；
• 从右到左维护一个最小值 ，在进入左段之前，遍历到的都是大于 的，我们要求的是遍历中最后一个大于 元素的位置。

复杂度分析

时间复杂度：，其中 是给定数组的长度，我们仅需要遍历该数组一次。

空间复杂度：,我们只需要常数的空间保存若干变量。

官方代码

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        // 初始化
        int len = nums.length;
        int min = nums[len-1];
        int max = nums[0];
        int begin = 0, end = -1;
        // 遍历
        for(int i = 0; i < len; i++){
            if(nums[i] < max){          
                end = i;                // 从左到右维持最大值，寻找右边界 end
            }else{
                max = nums[i];
            }
            if(nums[len-i-1] > min){    
                begin = len-i-1;        // 从右到左维持最小值，寻找左边界 begin
            }else{
                min = nums[len-i-1];
            }            
        }
        return end-begin+1;
    }
}