首先,关于单链表中的环,一般涉及到一下问题:
1. 解题思路:判断链表是否有环(哈希表)
最容易想到的方法是遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
具体地,我们可以使用哈希表来存储所有已经访问过的节点。
- 每次我们到达一个节点
- 如果该节点已经存在于哈希表中,则说明该链表是环形链表
- 否则就将该节点加入哈希表中。
- 重复这一过程,直到我们遍历完整个链表即可。
复杂度分析
时间复杂度: ,其中
是链表中的节点数。最坏情况下我们需要遍历每个节点一次。
空间复杂度: ,其中
是链表中的节点数。主要为哈希表的开销,最坏情况下我们需要将每个节点插入到哈希表中一次。
整理的代码
public class Solution {public boolean hasCycle(ListNode head) {//1.使用hash表进行存储Set<ListNode> seen = new HashSet<ListNode>();while (head != null) {if (!seen.add(head)) {return true;}head = head.next;}return false;}}
1. 解题思路:判断链表是否有环(快慢指针)
本方法需要读者对「Floyd 判圈算法」(又称龟兔赛跑算法)有所了解。
假想「乌龟」和「兔子」在链表上移动,「兔子」跑得快,「乌龟」跑得慢。
- 当「乌龟」和「兔子」从链表上的同一个节点开始移动时
- 如果该链表中没有环,那么「兔子」将一直处于「乌龟」的前方;
- 如果该链表中有环,那么「兔子」会先于「乌龟」进入环,并且一直在环内移动 。
- 等到「乌龟」进入环时,由于「兔子」的速度快,它一定会在某个时刻与乌龟相遇 。
我们可以根据上述思路来解决本题。具体地,我们定义两个指针,一快一满。慢指针每次只移动一步,而快指针每次移动两步。🍗【重要】初始时,慢指针在位置 head,而快指针在位置 head.next。这样一来,如果在移动的过程中,快指针反过来追上慢指针,就说明该链表为环形链表。否则快指针将到达链表尾部,该链表不为环形链表。
为什么我们要规定初始时慢指针在位置 head,快指针在位置 head.next,而不是两个指针都在位置 head ?
观察下面的代码,我们使用的是 while 循环,循环条件先于循环体。由于循环条件一定是判断快慢指针是否重合,如果我们将两个指针初始都置于 head,那么 while 循环就不会执行。因此,我们可以假想一个在 head 之前的虚拟节点,慢指针从虚拟节点移动一步到达 head,快指针从虚拟节点移动两步到达 head.next,这样我们就可以使用 while 循环了。
当然,我们也可以使用 do-while 循环。此时,我们就可以把快慢指针的初始值都置为 head。
复杂度分析
时间复杂度: ,其中
是链表中的节点数。
- 当链表中不存在环时,快指针将先于慢指针到达链表尾部,链表中每个节点至多被访问两次。- 当链表中存在环时,每一轮移动后,快慢指针的距离将减小一。而初始距离为环的长度,因此至多移动  轮。
空间复杂度: ,我们只使用了两个指针的额外空间。
整理的代码
public class Solution {
public boolean hasCycle(ListNode head) {
//1.没有结点或者只有1个结点且没闭环
if (head == null || head.next == null) return false;
//2.初始化slow,fast
ListNode slow = head;
ListNode fast = head.next;
//3.只要二者没相遇就跑
while (slow != fast) {
//除非遇到链表的结尾
if (fast == null || fast.next == null) {
return false;
}
slow = slow.next;
fast = fast.next.next;
}
return true;
}
}
2. 解题思路:找链表环的入口
给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
示例 1: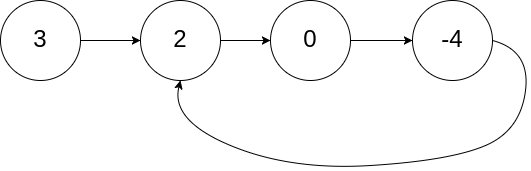
输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2: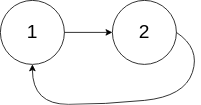
输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。
算法流程:
双指针第一次相遇: 设两指针 fast,slow 指向链表头部 head,fast 每轮走 2 步,slow 每轮走 1 步;
第一种结果: fast 指针走过链表末端,说明链表无环,直接返回
null;若有环,两指针一定会相遇。因为每走 1 轮,fast 与 slow 的间距 +1,fast 终会追上 slow;
第二种结果: 当 fast == slow 时, 两指针在环中 第一次相遇 。
下面分析此时 fast 与 slow走过的 步数关系 :
设链表共有 a+b 个节点,其中 链表头部到链表入口 有 a 个节点(不计链表入口节点), 链表环 有 b 个节点(这里需要注意,a 和 b 是未知数,例如图解上链表 a=4 , b=5);设两指针分别走了 f ,s 步,则有:
**fast**走的步数是**slow**步数的 2 倍,即f = 2s;(解析: fast 每轮走 2 步)
**fast**比**slow**多走了 n 个环的长度,即**f = s + nb**;( 解析: 双指针都走过
**a**步,然后在环内绕圈直到重合,重合时fast比slow多走 环的长度整数倍 );以上两式相减得:
**f=2nb,s = nb**,即 fast 和 slow 指针分别走了 2n,n 个 环的周长 (注意: n 是未知数,不同链表的情况不同)。
目前情况分析:
如果让指针从链表头部一直向前走并统计步数 k ,那么所有 走到链表入口节点时的步数 是:k = a + nb
(先走 a 步到入口节点,之后每绕 1 圈环( b 步)都会再次到入口节点)。
而目前,slow 指针走过的步数为
_nb_步。因此,我们只要想办法让 slow 再走 a 步停下来,就可以到环的入口。- 但是我们不知道 a 的值,该怎么办?
依然是使用双指针法。我们构建一个指针:此指针和 slow 一起向前走 a 步后,两者在入口节点重合。 那么从哪里走到入口节点需要
**a**步? 答案:链表头部 head 。
双指针第二次相遇:
slow指针 位置不变 ,将 fast 指针重新 指向链表头部节点 ;slow 和 fast 同时每轮向前走 1 步;
TIPS:此时
f = 0,s = nb;当 fast 指针走到 f = a 步时,slow 指针走到步 s=a+nb ,此时 两指针重合,并同时指向链表环入口
第二次相遇后,返回 slow 指针指向的节点即可。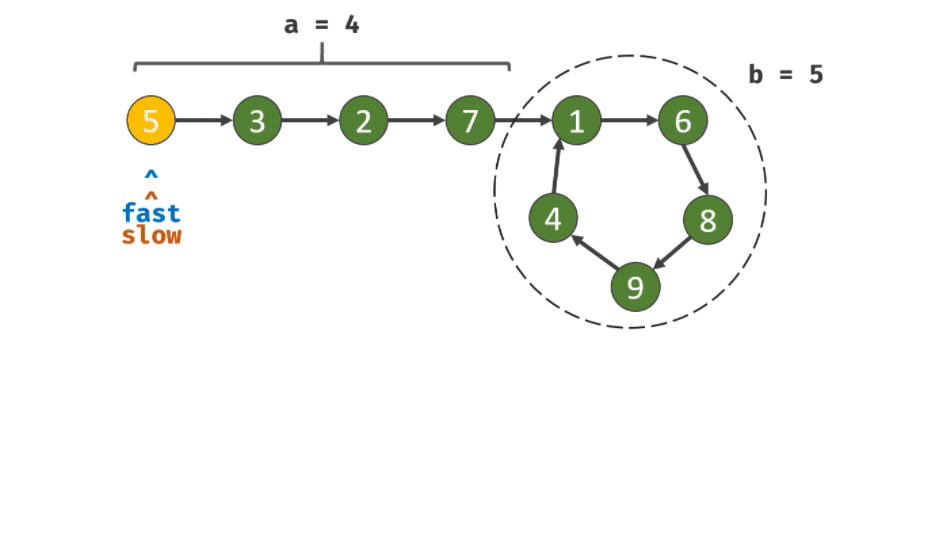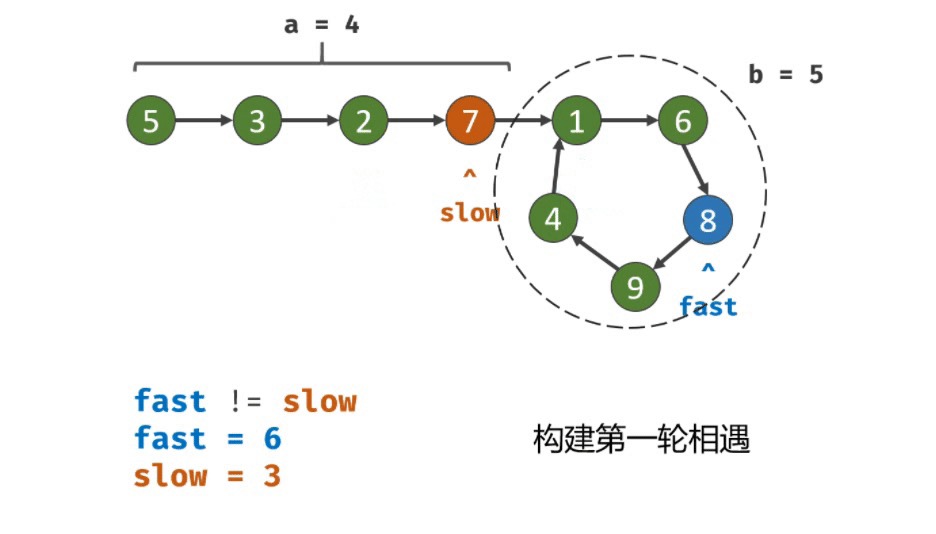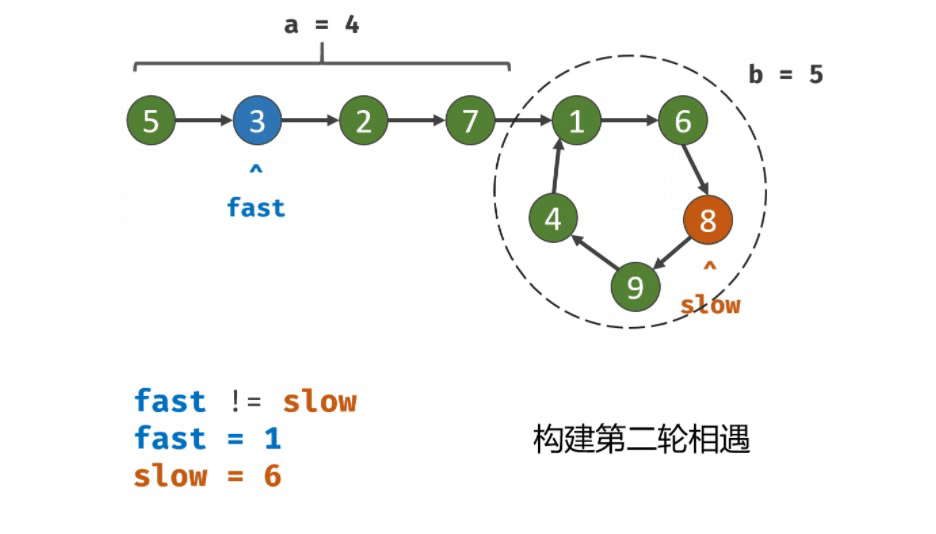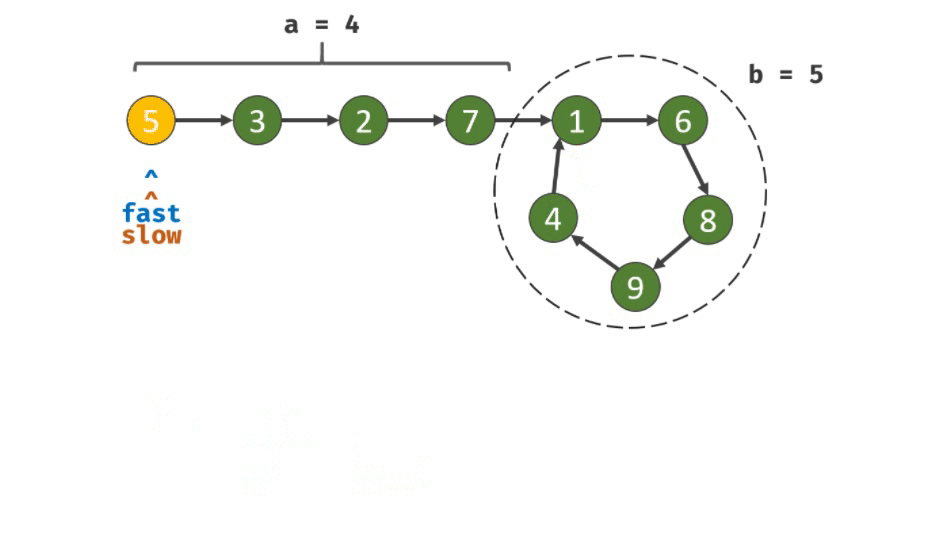
复杂度分析
时间复杂度: ,其中
是链表的长度。
第二次相遇中,慢指针须走步数 a < a + b;第一次相遇中,慢指针须走步数 a+b−x<a+b,其中 x 为双指针重合点与环入口距离;因此总体为线性复杂度。
空间复杂度: ,双指针使用常数大小的额外空间。
整理的代码
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast = head, slow = head;
while (true) {
if (fast == null || fast.next == null) return null;
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;
}
fast = head;
while (fast != slow) {
slow = slow.next;
fast = fast.next;
}
return fast;
}
}
3. 解题思路:求环上节点的个数;
算法流程:
- 判断是否有环
- 有环 fast==slow
- 无环 fast==null || fast.next==null
- fast 在环内重新跑一圈跑到 slow 处,跑过的节点数就是环的结点数
整理的代码
public class Solution {
public int detectCycleNumber(ListNode head) {
ListNode fast = head, slow = head;
while (true) {
if (fast == null || fast.next == null) return 0;
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;
}
fast = slow.next;
int num=1;
while (fast != slow) {
num++;
fast = fast.next;
}
return num;
}
}
4. 解题思路:求链表的长度;
算法流程:
a+b 就是链表的长度,环外长度+环内长度
- 判断是否有环
- 有环 fast==slow
- 无环 fast==null || fast.next==null
- 通过计算可知,当 fast=head ,fast 和 slow 重新开始跑动,步长为 1 ,相遇时结点数为环外结点数
**a** - fast 在环内重新跑一圈跑到 slow 处,跑过的节点数就是环内的结点数
**b**
整理的代码
public class Solution {
public ListNode isCycle(ListNode head){
ListNode fast = head, slow = head;
while (true) {
if (fast == null || fast.next == null) return null;
fast = fast.next.next;
slow = slow.next;
if (fast == slow) return slow;
}
}
public int detectCycle(ListNode head) {
ListNode fast = head, slow = isCycle(head);
int res=0;
if(slow==null){//说明无环
while(fast!=null){
res++;
fast=fast.next;
}
return res;
}
//有环 a 步
while (fast != slow) {
res++;
slow = slow.next;
fast = fast.next;
}
//环内 b 步
fast=fast.next;
while(fast!=slow){
res++;
fast=fast.next;
}
return res+1;
}
}
5. 解题思路:求出环上距离任意一个节点最远的点(对面节点)
如下图所示,点1和4、点2和5、点3和6分别互为 "对面节点" ,也就是换上最远的点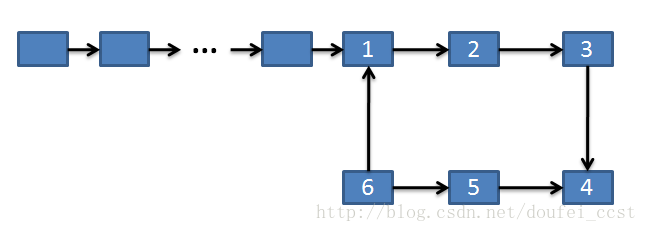
如下图,我们想像一下,把环从ptro处展开,展开后可以是无限长的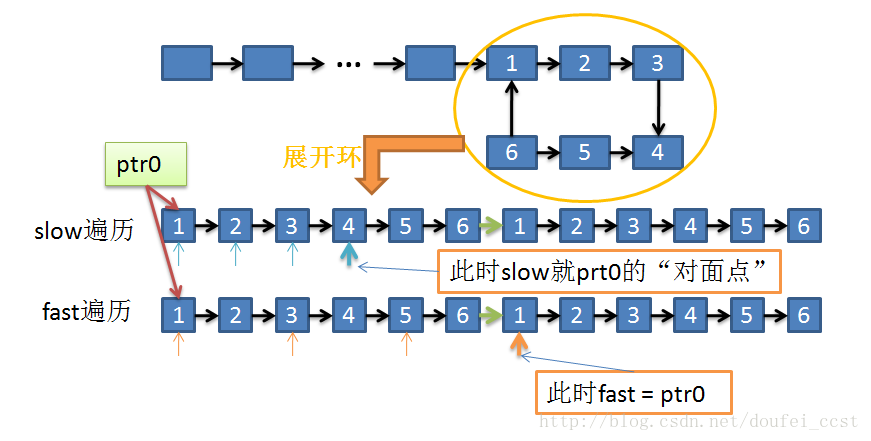
可以这样思考:同样使用上面的快慢指针的方法,让 slow 和 fast 都指向 ptr0,每一步都执行与上面相同的操作
slow 每次跳一步,fast 每次跳两步
当 fast = ptr0 (偶数)或者 fast = prt0->next (奇数)的时候 slow 所指向的节点就是 ptr0 的 "对面节点" 。
偶数、奇数指的是 环内节点数
由于 slow 移动的速度是 fast 的一半,相同的时间内,当 fast 遍历完整个环长度 个节点的时候 slow 正好遍历了
个节点 。
因此求解某节点的最远距离,就是 slow 和 fast 以某节点作为起点,跑一圈,slow 指向就是其最远距离。
6. 解题思路:(扩展)如何判断两个无环链表是否相交
7. 解题思路:(扩展)如果相交,求出第一个相交的节点
问题转化:求解环的入口结点
问题6 和 问题7,其实就是做一个问题的转化:
假设有链表 listA 和 listB,如果两个链表都无环,并且有交点,那么我们可以让其中一个链表(不妨设是listA)的为节点连接到其头部,这样上述情况对于 listB 来说就一定会出现一个环。
另类解题思路
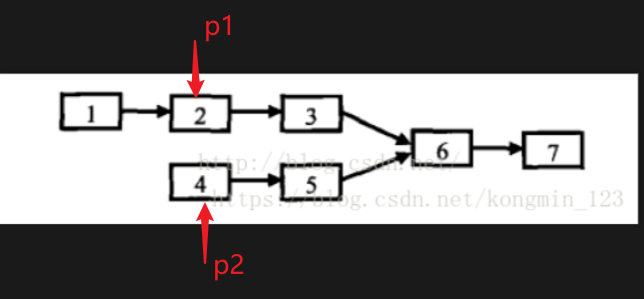
能知道链表长度那么遍历一下便可以求出来,就像上图,我们知道 1结点 无效,从 2结点 和 4结点 开始遍历。但是题目是无法知道那个链表长、那个链表短、以及具体长度的。那么怎么才能将指针定位成上图这个样子呢?
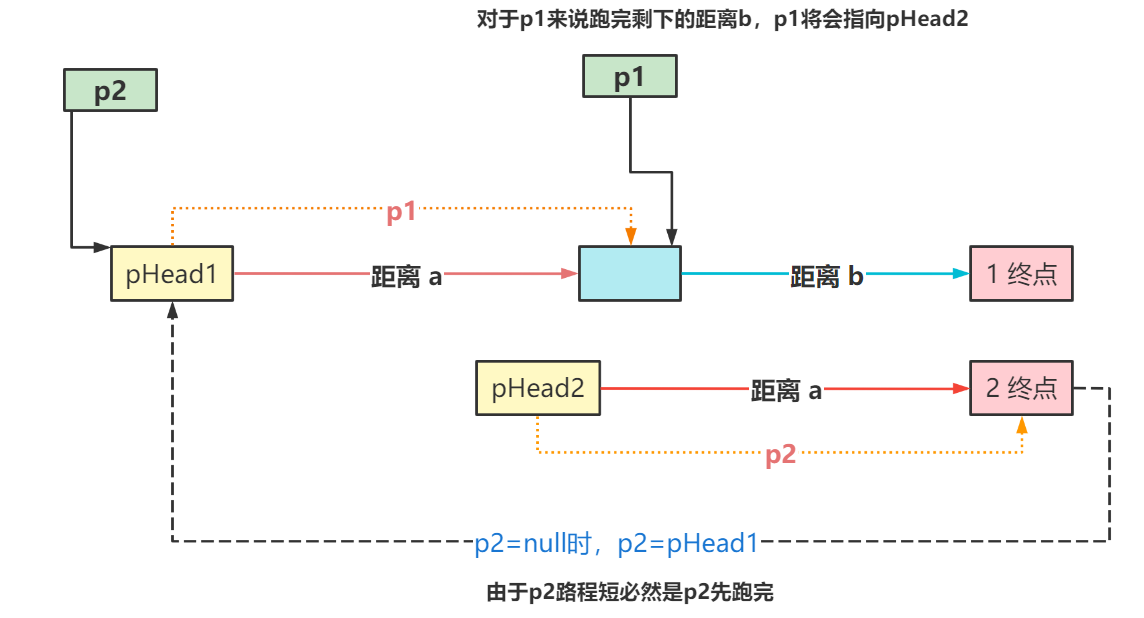
首先 长链表 假设长度 a+b ,短链表 假设长度 a,那么差值是 b。
- 当长短链表一起顺序遍历,短链表遍历到结尾的时候,双方走过的距离是 a ,长链表剩余 b 距离未走
- 将走完的 p2 指向 pHead1 时,跟随着 p1 顺序遍历,当 p1=null 时,说明走过了多余的 b 距离
- 此时将 p1 指向 pHead2 ,双方都剩余 a 距离未走,得到想要的情况
双方都剩余 a 距离未走,得到想要的情况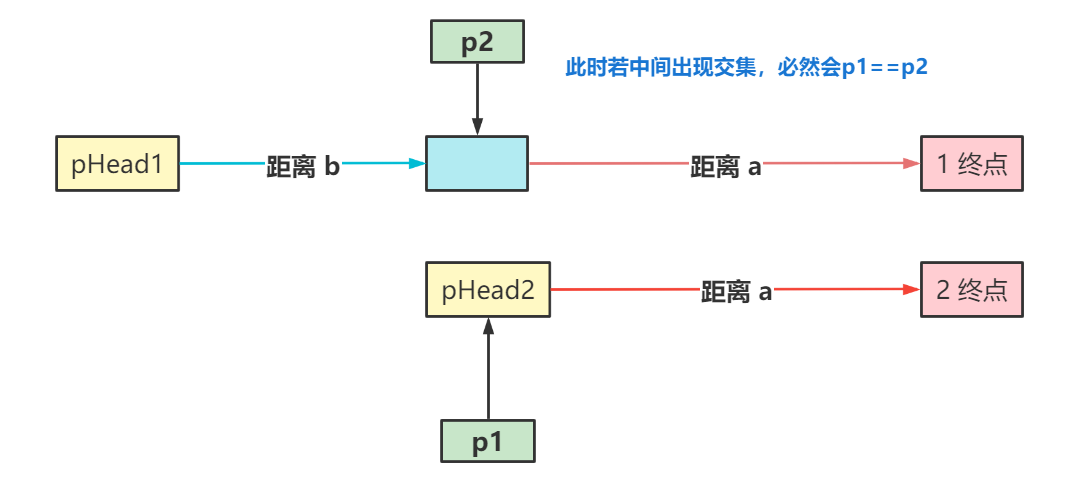
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA==null||headB==null)return null;
ListNode pA=headB;
ListNode pB=headA;
while(pA!=pB){
pA = (pA == null) ? headA : pA.next;
pB = (pB == null) ? headB : pB.next;
}
return pA;
}
}

