🚩[LeetCode]Ar204. 计数质数

🚩传送门：https://leetcode-cn.com/problems/count-primes/

题目

统计所有小于非负整数 n 的质数的数量。

示例 1：

输入：n = 10 输出：4 解释：小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

示例 2：

输入：n = 0 输出：0

示例 3：

输入：n = 1 输出：0

📖 前言

统计 [2,n] 中质数的数量是一个很常见的题目

解题思路：暴力枚举

很直观的思路是我们枚举每个数判断其是不是质数。

质数的定义：在大于 的自然数中，除了 和它本身以外不再有其他因数的自然数。因此对于每个数 ，我们可以从小到大枚举 中的每个数 ，判断 是否为 的因数。但这样判断一个数是否为质数的时间复杂度最差情况下会到 ，无法通过所有测试数据。

🟢 由 ，考虑到如果 y 是 x 的因数，那么 也必然是 x 的因数，因此我们只要校验 y 或者 即可。而如果我们每次选择校验两者中的较小数，则不难发现较小数一定落在 [2,x] 的区间中，因此我们只需要枚举[2,x] 中的所有数即可，这样单次检查的时间复杂度从 降低至了 。
解释：

复杂度分析

时间复杂度：

单个数检查的时间复杂度为 ，一共要检查 个数，因此总时间复杂度为 。

空间复杂度：

官方代码

class Solution {
    public int countPrimes(int n) {
        int ans = 0;
        for (int i = 2; i < n; ++i) {
            ans += isPrime(i) ? 1 : 0;
        }
        return ans;
    }
    public boolean isPrime(int x) {
        //i*i相当于 y
        for (int i = 2; i * i <= x; ++i) {
            if (x % i == 0) {
                return false;
            }
        }
        return true;
    }
}

解题思路：埃氏筛

枚举没有考虑到数与数的关联性，因此难以再继续优化时间复杂度。接下来我们介绍一个常见的算法，该算法由希腊数学家厄拉多塞（）提出，称为厄拉多塞筛法，简称埃氏筛。

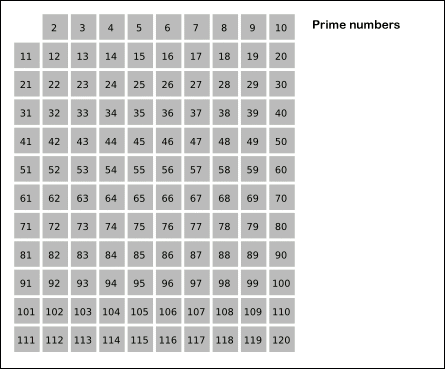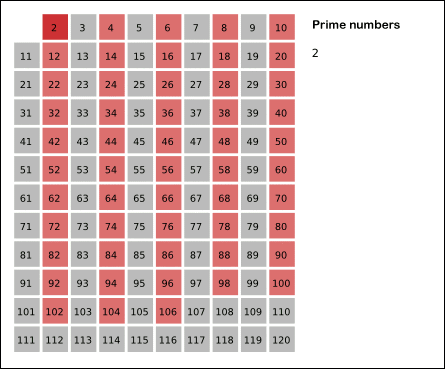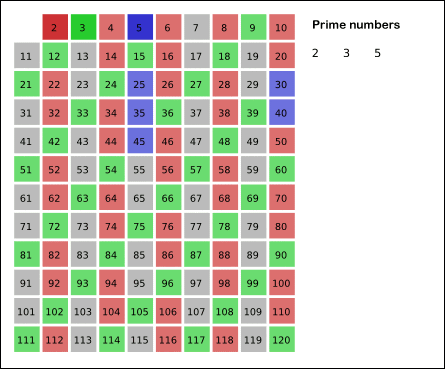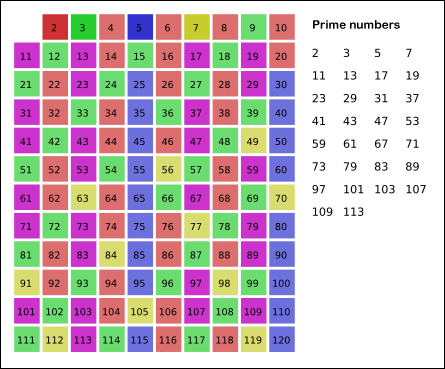
我们考虑这样一个事实：如果 是质数，那么大于 的 的倍数 一定不是质数，因此我们可以从这里入手。

我们设 表示数 是不是质数，如果是质数则为 ，否则为 。从小到大遍历每个数，如果这个数为质数，则将其所有的倍数都标记为合数（除了该质数本身），即 ，这样在运行结束的时候我们即能知道质数的个数。

这种方法的 正确性 是比较显然的：这种方法显然不会将质数标记成合数；另一方面，当从小到大遍历到数 x 时，倘若它是合数，则它一定是某个小于 x 的质数 y 的整数倍，故根据此方法的步骤，我们在遍历到 y 时，就一定会在此时将 x 标记为 isPrime[x]=0。因此，这种方法也不会将合数标记为质数。

🚩当然这里还可以继续 优化，对于一个质数 x，如果按上文说的我们从 2x 开始标记其实是 冗余 的，应该直接从 开始标记，因为 这些数一定在 x 之前就被其他数的倍数标记过了。

因为假设当前数字为 7 ，它需要标记的数字是从7×7开始，这是因为**6**×7，**5**×7，**4**×7，**3**×7，**2**×7 在先前的过程中一定已被标记。红色6虽然是合数，但是它可以拆分因此也被标记，蓝色一定过来时被标记。

复杂度分析

时间复杂度：

具体证明这里不再展开，读者可以自行思考或者上网搜索，本质上是要求解 的和，其中 为质数。当然我们可以了解这个算法一个比较松的上界 怎么计算，这个等价于考虑 的和，而 ，而 到 中所有数的倒数和趋近于 ，因此

空间复杂度： 。我们需要 的空间记录每个数是否为质数。

官方代码

class Solution {
    public int countPrimes(int n) {
        int[] isPrime = new int[n];
        Arrays.fill(isPrime, 1);
        int ans = 0;
        for (int i = 2; i < n; ++i) {
            if (isPrime[i] == 1) {
                ans += 1;
                //着手标记自身的倍数
                if ((long) i * i < n) {
                    for (int j = i * i; j < n; j += i) {
                        isPrime[j] = 0;
                    }
                }
            }
        }
        return ans;
    }
}

✍杂谈：

上面运用厄拉多塞筛法求一定范围内的质数已经十分 高效 了。然而，我们使用布尔数组标记一个数是否为质数时，每个值都占用了一个字节（Byte）。但是，我们仅需要两个不同的值来表示是否为质数即可。即一个比特（bit）来表示即可（0、1）。如果这样的话，我们便最优可节省八分之七的空间（还得结合实际情况）。

解题思路：线性筛

埃氏筛其实还是存在冗余的标记操作，比如对于 45 这个数，它会同时被 3,5 两个数标记为合数，因此我们优化的目标是让每个合数只被标记一次，这样时间复杂度即能保证为 O(n)，这就是我们接下来要介绍的线性筛。

相较于埃氏筛，我们多维护一个 primes 数组表示当前得到的质数集合。我们从小到大遍历，如果当前的数 x 是质数，就将其加入 primes 数组。

与埃氏筛不同的是，「标记过程」不再仅当 为质数时才进行，而是对每个整数 都进行。
对与整数 ，我们不再标记其所有的倍数 ，而是只标记质数集合中的数与 相乘的数，即 且在发现 的时候结束当前标记。

🚩核心点在于：如果 可以被 整除（），那么对于合数 而言，它一定在后面遍历到 这个数的时候被标记，其他同理，这保证了每个合数只会被其「最小的质因数」筛去，即每个合数被标记一次。

👉解释： 这是由于 ，所以后面遍历的过程中一定会轮到 去和 做乘法。

线性筛还有其他拓展用途，有能力的读者可以搜索关键字「积性函数」继续探究如何利用线性筛来求解积性函数相关的题目。

✍线性筛原理：

根据《算术基本定理》：每一个合数都可以以唯一形式被写成质数的乘积。

换言之两个或两个以上质数的乘积，只会组成一个合数

n 以内，从 2 起，将遇到的每一个数与质数数组中每一个数相乘

数为质数：质数 × 质数 = 合数 数为合数：合数可拆为质数 × 质数 ... = 质数 × 质数 ... × 质数 = 合数

复杂度分析

时间复杂度：

空间复杂度：

官方代码

class Solution {
    public int countPrimes(int n) {
        //1. 定义质数数组
        List<Integer> primes = new ArrayList<Integer>();
        //2. 质数标记数组
        int[] isPrime = new int[n];
        Arrays.fill(isPrime, 1);
        for (int i = 2; i < n; ++i) {
            if (isPrime[i] == 1) {
                primes.add(i);
            }
            //3. 将当前数 i 与每一个质数数组中的数相乘
            for (int j = 0; j < primes.size() && i * primes.get(j) < n; ++j) {
                isPrime[i * primes.get(j)] = 0;
                //4. 灵性的剪枝
                if (i % primes.get(j) == 0) {
                    break;
                }
            }
        }
        return primes.size();
    }
}