[LeetCode]Dp467 环绕字符串中唯一子字符串

🚩传送门：https://leetcode-cn.com/problems/unique-substrings-in-wraparound-string/

题目

把字符串 s 看作是 "abcdefghijklmnopqrstuvwxyz" 的无限环绕字符串，所以 s 看起来是这样的的一串 "...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd...."现在我们有了另一个字符串 p 。你需要的是找出 s 中有多少个唯一的 p 的非空子串，尤其是当你的输入是字符串 p ，你需要输出字符串 s 中 p 的不同的非空子串的数目 。

注意： p 仅由小写的英文字母组成，p 的大小可能超过 10000。

示例 1:

输入: “a” 输出: 1 解释: 字符串 S 中只有一个”a”子字符。

示例 2:

输入: “cac” 输出: 2 解释: 字符串 S 中的字符串”cac”只有两个子串”a”、”c”。

示例 3:

输入: “zab” 输出: 6 解释: 在字符串 S 中有六个子串”z”、”a”、”b”、”za”、”ab”、”zab”。

解题思路：动态规划

由于字符串S是无限环绕字符串，不难想象字符串应该如同字母组成的环一样。如图

要得到不同的非空子串，每个非空子串自身就必须是 连续 的。可以找出最长连续串，然后加上不在最长连续串中的 零散 的字符串 。

如例：zcdeabcdef，最长连续串为abcdef，零散串为z和cde,但cde被最长连续串abcdef覆盖。

连续性如何判断 ？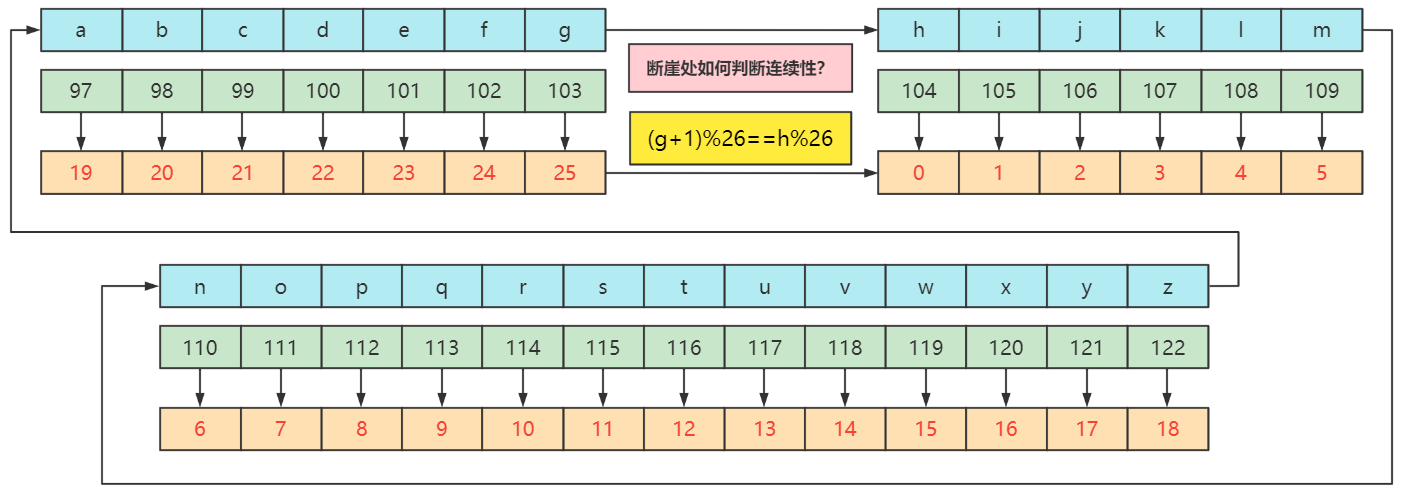

如何求解 ？

最初想法
为每一特定串标记连续性（即空间复杂度），在 时间复杂度内完成，标记成功后会变成组合总数求解问题，但有个问题需解决，即 覆盖 问题，若要解决覆盖问题则需要多余的遍历次数，要不停检查 小串 是否被 大串 覆盖，需要耗费 的时间复杂度，显然效果过差 。

大佬想法 （🤣牛逼特斯拉）
标记连续性，但是是 空间复杂度，串的差异性与 表无关，且在 时间复杂度内完成。创建 26 长度的 dp 表，对应字母放入对应位置的 dp 表中，若是连续的则递增，小串无法刷新掉大串长度 🦄真尼玛鬼才。


…..

👉 定义 为以字符串 做结尾的连续字符串的长度

👉 初始化

状态转移方程：

     **与上一个字符成连续**<br />         **与上一个字符不连续**

复杂度分析

时间复杂度：，其中 为数组 的长度

空间复杂度：，只需要26个英文字母的表即可。

代码

官方代码

class Solution {
    public:
        int findSubstringInWraproundString(string p) {
            vector<int> dp(26,0);
            int num=0;
            int result=0;
            for (int i =0; i<p.size(); i++) {
        // 由于串是环状的,a-z的ascii码范围97-122,两边都需要%26
                if(i>0 &&((p[i-1]+1)%26==p[i]%26)){
                    ++num;
                }else{
          //第一个元素不需要考虑连续性
                    num=1;
                }
        // p[i]-'a'是得到对应dp数组下标
                dp[p[i]-'a'] = max(dp[p[i]-'a'],num);
            }
      // 将所有增量累加，就是答案
            return accumulate(dp.begin(),dp.end(),0);
        }
}