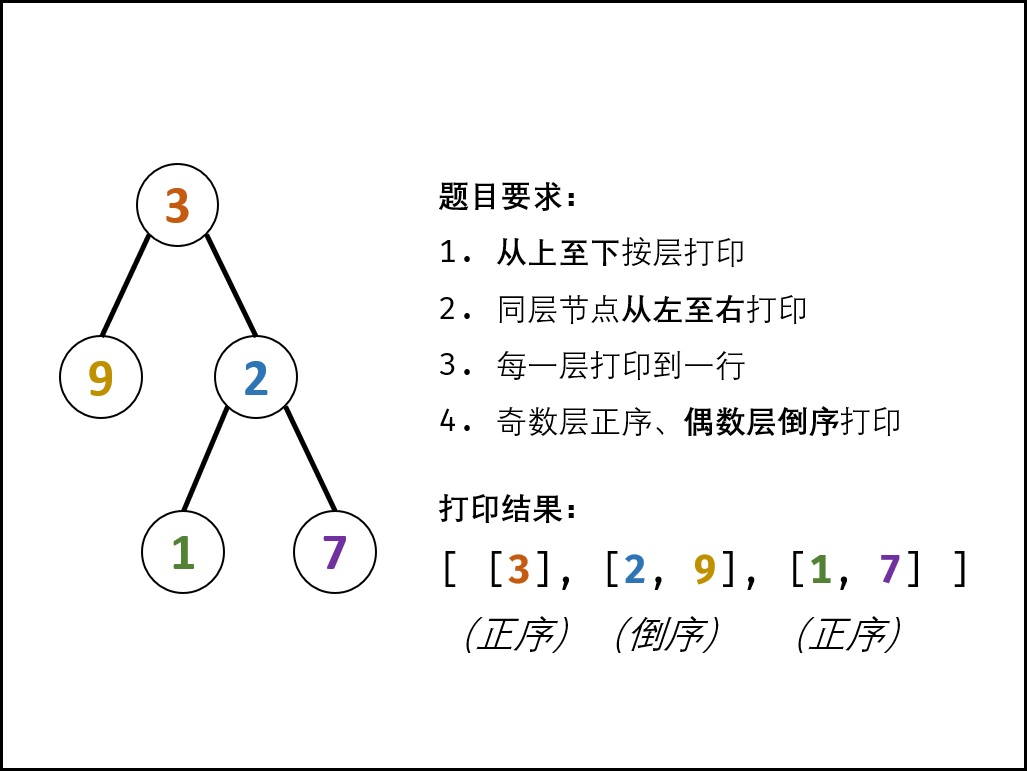题目

分别按照二叉树先序，中序和后序打印所有的节点。

示例 1:

输入: {1，2，3} 输出: [[1,2,3],[2,1,3],[2,3,1]]

解题思路：递归 [先序、中序、后序]

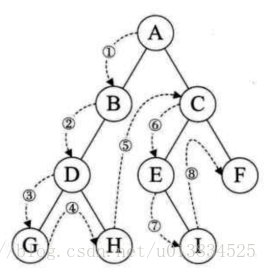
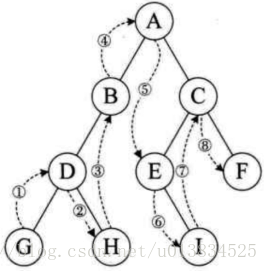
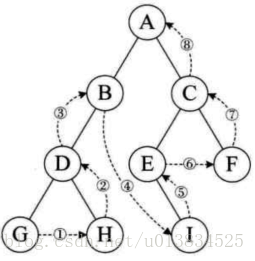
🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图1🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图2🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图3
先序 中序 后序

  1. import java.util.*;
  3. public class Solution {
  5.     public class TreeNode {
  6.         int val = 0;
  7.         TreeNode left = null;
  8.         TreeNode right = null;
  9.     }
  11.     public int[][] threeOrders (TreeNode root) {
  12.         //三个集合，分别存储三种遍历结果
  13.         List<Integer> preList = new ArrayList<>();
  14.         List<Integer> inList = new ArrayList<>();
  15.         List<Integer> postList = new ArrayList<>();
  17.         //调用函数计算遍历结果
  18.         preOrder(root, preList);
  19.         inOrder(root, inList);
  20.         postOrder(root, postList);
  22.         //存放结果集
  23.         int[][] res = new int[3][preList.size()];
  24.         for(int i = 0; i < preList.size(); i++){
  25.             res[0][i] = preList.get(i);
  26.             res[1][i] = inList.get(i);
  27.             res[2][i] = postList.get(i);
  29.         }
  30.         //答案返回
  31.         return res;
  32.     }
  33.     // 先序遍历函数
  34.     public void preOrder(TreeNode root, List<Integer> list){
  35.         //特判
  36.         if(root == null) return;
  37.         //对左右子树进行递归的遍历
  38.         list.add(root.val);
  39.         preOrder(root.left, list);
  40.         preOrder(root.right, list);
  41.     }
  43.     // 中序遍历函数
  44.     public void inOrder(TreeNode root, List<Integer> list){
  45.         //特判
  46.         if(root == null) return;
  47.         //递归调用：对左右子树进行递归的遍历
  48.         inOrder(root.left, list);
  49.         list.add(root.val);
  50.         inOrder(root.right, list);
  51.     }
  53.     // 后序遍历函数
  54.     public void postOrder(TreeNode root, List<Integer> list){
  55.         if(root == null) return;
  56.         //递归调用：对左右子树进行递归的遍历
  57.         postOrder(root.left, list);
  58.         postOrder(root.right, list);
  59.         list.add(root.val);
  60.     }
  61. }

解题思路：队列 [层次]

🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图4
层次遍历的步骤是：

  1. 对于不为空的结点，先把该结点加入到队列中
  2. 从队中拿出结点，如果该结点的左右结点不为空，就分别把左右结点加入到队列中
  3. 重复以上操作直到队列为空
  1. public class Solution{
  2.     class TreeNode {
  3.         int val;
  4.         TreeNode left;
  5.         TreeNode right;
  6.         TreeNode(int x) { val = x; }
  7.     }
  9.      public void levelIterator(TreeNode root)
  10.      {
  11.          if(root == null)  return ;
  12.          //1.创建队列
  13.          LinkedList<TreeNode> queue = new LinkedList<>();
  14.          TreeNode current = null;
  15.          queue.offer(root);//将根节点入队
  16.          while(!queue.isEmpty())
  17.          {
  18.              current = queue.poll();                //出队并获取队头元素
  19.              System.out.print(current.val +"-->");    //访问刚出队的对头元素
  20.              if(current.left != null)                //如果当前节点的左节点不为空，将其入队
  21.                  queue.offer(current.left);
  22.              if(current.right != null)                //如果当前节点的右节点不为空，将其入队
  23.                 queue.offer(current.right);
  24.          }
  25.      }
  26. }

解题思路：双栈 [之字型]

给定的二叉树是 {1,2,3,#,#,4,5}

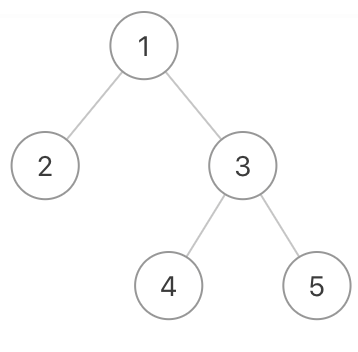
🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图5

该二叉树之字形层序遍历的结果是

[ [1], [3,2], [4,5] ]

使用两个栈去实现。奇数行使用 stack1，偶数行使用 stack2。

注：使用 stack1 时，按照左右的顺序存储；使用 stack2 时，按照右左的顺序存储

  1. ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
  2.     ArrayList<ArrayList<Integer>> list = new ArrayList<ArrayList<Integer>>();
  3.     if(pRoot==null)
  4.         return list;
  5.     Stack<TreeNode> stack1 = new Stack<TreeNode>();
  6.     Stack<TreeNode> stack2 = new Stack<TreeNode>();
  7.     stack1.add(pRoot);
  8.     while(!stack1.empty() || !stack2.empty()){
  9.         ArrayList<Integer> li = new ArrayList<Integer>();
  10.         if(!stack1.empty()){
  11.             while(!stack1.empty()){
  12.                 TreeNode node = stack1.pop();
  13.                 li.add(node.val);
  14.                 if(node.left!=null)
  15.                     stack2.add(node.left);
  16.                 if(node.right!=null)
  17.                     stack2.add(node.right);
  18.             }
  19.             list.add(li);
  20.         }
  21.         else if(!stack2.empty()){
  22.             while(!stack2.empty()){
  23.                 TreeNode node = stack2.pop();
  24.                 li.add(node.val);
  25.                 if(node.right!=null)
  26.                     stack1.add(node.right);
  27.                 if(node.left!=null)
  28.                     stack2.add(node.left);
  29.             }
  30.             list.add(li);
  31.         }
  32.     }
  33.     return list;
  34. }

解题思路：队列层次遍历+双端队列 [之字型]

🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图6

复杂度分析

时间复杂度：🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图7，其中 🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图8 为二叉树的节点数量，即 BFS 需循环 🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图9 次，占用 🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图10 ；

  1.   - 双端队列的队首和队尾的添加和删除操作的时间复杂度均为  ![](https://cdn.nlark.com/yuque/__latex/5e079a28737d5dd019a3b8f6133ee55e.svg#card=math&code=O%281%29&height=20&id=FWqwL) 。

空间复杂度：🍗实现二叉树先序、中序、后序、层次、之字型遍历合集 - 图11

  1.   - 最差情况下，即当树为满二叉树时，最多有  ![](https://cdn.nlark.com/yuque/__latex/c53191173d224aa0c56749fb3bce82f7.svg#card=math&code=%5Cfrac%7Bn%7D%7B2%7D&height=12&id=loMeW)  个树节点 同时 在 **队列 **中

整理代码

  1. class Solution {
  2.     public List<List<Integer>> levelOrder(TreeNode root) {
  3.         //1. 队列用于层次遍历
  4.         Queue<TreeNode> queue = new LinkedList<>();
  5.         //2. res 结果集用于存储结果
  6.         List<List<Integer>> res = new ArrayList<>();
  7.         //3. 先添加根节点
  8.         if(root != null) queue.add(root);
  9.         //# 当队列不为空
  10.         while(!queue.isEmpty()) {
  11.             //4. 双端队列，用于正序、倒序存储某一层
  12.             LinkedList<Integer> list = new LinkedList<>();
  13.             for(int i = queue.size(); i > 0; i--) {
  14.                 TreeNode node = queue.poll();
  15.                 //由在结果集中的层次来断定正序、倒序
  16.                 if(res.size() % 2 == 0) 
  17.                     list.addLast(node.val);         // 偶数层 -> 队列尾部
  18.                 else 
  19.                     list.addFirst(node.val);         // 奇数层 -> 队列头部
  20.                 //5. 将左右子树入队
  21.                 if(node.left != null) queue.add(node.left);
  22.                 if(node.right != null) queue.add(node.right);
  23.             }
  24.             res.add(list);
  25.         }
  26.         return res;
  27.     }
  28. }

我的代码

  1. public class Solution {
  2.     public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
  3.         //1. 队列用于层次遍历
  4.         Queue<TreeNode>queue=new LinkedList<>();
  5.         //2. res 结果集用于存储结果
  6.         ArrayList<ArrayList<Integer> > res = new ArrayList<>();
  7.         //3. 先添加根节点
  8.         if(pRoot != null) queue.add(pRoot);
  9.         while(!queue.isEmpty()){
  10.             int size=res.size()+1;
  11.             //4. 双端队列，用于正序、倒序存储某一层
  12.             LinkedList<Integer> list=new LinkedList<>();
  13.             for(int i=queue.size();i>0;i--){
  14.                 TreeNode node=queue.poll();
  15.                 //5. 与运算符判断奇偶
  16.                 if((size&1)==1){
  17.                     list.addLast(node.val);        
  18.                 }else{
  19.                     list.addFirst(node.val);
  20.                 }
  21.                 if(node.left!=null)queue.add(node.left);
  22.                 if(node.right!=null)queue.add(node.right);
  23.             }
  24.             //6. LinkedList 转换 ArrayList
  25.             res.add(new ArrayList<Integer>(list));
  26.         }
  27.         return res;
  28.     }
  29. }