[NC]138. 矩阵最长递增路径

🚩传送门：牛客题目
力扣题目

题目

给定一个 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外

示例 1：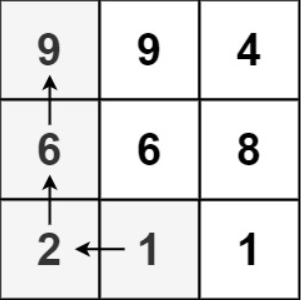

输入：matrix = [[9,9,4],[6,6,8],[2,1,1]] 输出：4
解释：最长递增路径为 [1, 2, 6, 9]。

解题思路：DFS

从一个单元格开始进行深度优先搜索，即可找到从该单元格开始的最长递增路径。对每个单元格分别进行深度优先搜索之后，即可得到矩阵中的最长递增路径的长度。

但是如果使用朴素深度优先搜索，时间复杂度是指数级，会超出时间限制，因此必须加以优化。

朴素深度优先搜索的时间复杂度过高的原因是进行了大量的重复计算，同一个单元格会被访问多次，每次访问都要重新计算。由于同一个单元格对应的最长递增路径的长度是固定不变的，因此可以使用记忆化的方法进行优化。用矩阵 dp 作为缓存矩阵，已经计算过的单元格的结果存储到缓存矩阵中。

使用记忆化深度优先搜索，当访问到一个单元格 (i,j) 时，如果 dp[i][j]≠0 ，说明该单元格的结果已经计算过，则直接从缓存中读取结果，如果 dp[i][j]=0，说明该单元格的结果尚未被计算过，则进行搜索，并将计算得到的结果存入缓存中。

遍历完矩阵中的所有单元格之后，即可得到矩阵中的最长递增路径的长度。

复杂度分析

时间复杂度： ，其中 和 分别是矩阵的行数和列数。

  - 深度优先搜索的时间复杂度是 ![](https://cdn.nlark.com/yuque/__latex/885872c14b6aac0cc7b5955da32370de.svg#card=math&code=O%28V%2BE%29&id=ncTHt)，其中 ![](https://cdn.nlark.com/yuque/__latex/9f493997c33913987175caf4a4849955.svg#card=math&code=V&id=zpkma) 是节点数， ![](https://cdn.nlark.com/yuque/__latex/321138a59e6eab0c97c21f05282a80a6.svg#card=math&code=E&id=crEU1) 是边数。
  - 在矩阵中， ![](https://cdn.nlark.com/yuque/__latex/e5681240ea63a71d57def5207ff67acd.svg#card=math&code=O%28V%29%3DO%28m%5Ccdot%20n%29&id=OugOl)，![](https://cdn.nlark.com/yuque/__latex/9016e2ced9d17b865452923468bd3953.svg#card=math&code=O%28E%29%3DO%284%C3%97m%5Ccdot%20n%29&id=DBQNT)

空间复杂度： ，其中 和 分别是矩阵的行数和列数。

我的代码

public class Solution {
    boolean CheckBorder(int[][] matrix, int i, int j) {
        if ((0 <= i && i < matrix.length) && (0 <= j && j < matrix[0].length))
            return true;
        return false;
    }
    public int DFS(int[][] matrix, int i, int j, int preNum, int[][] dp) {
        // 检查边界是否合法
        if (!CheckBorder(matrix, i, j)) return 0;
        // 检查是否递增,不递增说明当前结点不行
        if (matrix[i][j] <= preNum) return 0;
        // 检查当前结点是否被打过表，如果打过表直接返回
        if (dp[i][j] != 0) return dp[i][j];
        // 记录当前结点之后的递增序列
        int returnNum = 0;
        // 东南西北搜索
        int dir[][] = new int[][]{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        // 遍历四种搜索方向
        for (int k = 0; k < dir.length; k++) {
            returnNum = Math.max(returnNum, DFS(matrix, i + dir[k][0], j + dir[k][1], matrix[i][j], dp));
        }
        // 对当前结点进行打表
        dp[i][j] = returnNum + 1;
        return dp[i][j];
    }
    public int solve(int[][] matrix) {
        // write code here
        int dp[][] = new int[matrix.length][matrix[0].length];
        int res = 0;
        // 起点
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                // 对当前结点进行打表
                DFS(matrix, i, j, Integer.MIN_VALUE, dp);
                res = Math.max(res, dp[i][j]);
            }
        }
        return res;
    }
}