✍[LeetCode]dp97 交错字符

传送门：https://leetcode-cn.com/problems/interleaving-string/

题目

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错组成的。
两个字符串 s 和 t 交错的定义与过程如下，其中每个字符串都会被分割成若干非空子字符串：
s = s1 + s2 + ... + sn
t = t1 + t2 + ... + tm ，其中 **|n - m| <= 1** [ **没有这句很麻烦 **]
交错是：s1 + t1 + s2 + t2 + s3 + t3 + ...或 t1 + s1 + t2 + s2 + t3 + s3 + ...
提示：a + b 意味着字符串 a 和 b 连接。

示例 1：**

输入：s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac” 输出：true

示例 2：

输入：s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc” 输出：false

示例 3：**

输入：s1 = “”, s2 = “”, s3 = “” 输出：true

解题思路：动态规划

官方解释：**双指针错误**…..没看懂讲咩啊…废话一堆

记
代表 前 个元素与 前 个能否交错成 的前 个元素 。true 能 ，false 否 。

• 若 ，则 必然不可能由 与 交错而成
• 取 true 取决于以下两种情形：

  - ![](https://cdn.nlark.com/yuque/__latex/3d9e6310c08d511eaec447e3862c6a59.svg#card=math&code=dp%5Bi%20-%201%5D%5B%5C%20j%5C%20%5D%3Dtrue&height=20&width=140) 且  ![](https://cdn.nlark.com/yuque/__latex/67c98e9a8e579b377e5bfaa9c80c00fe.svg#card=math&code=s1%5Bi-1%5D%3Ds3%5Bi%2Bj-1%5D&height=20&width=170)s1和s3比的是第 i 个元素
  - ![](https://cdn.nlark.com/yuque/__latex/054e94923c04d38ba1cae44aba29f980.svg#card=math&code=dp%5B%5C%20i%5C%20%5D%5Bj-1%5D%3Dtrue&height=20&width=140) 且 ![](https://cdn.nlark.com/yuque/__latex/c9a94219bfb57e17d9acbb6401f19307.svg#card=math&code=s2%5Bj-1%5D%3Ds3%5Bi%2Bj-1%5D&height=20&width=172) s2和s3比的是第 J 个元素

复杂度分析

时间复杂度：， 为 的长度 ， 为 的长度。

空间复杂度：

代码

我的代码

public class Demo {
    public static boolean isInterleave(String s1, String s2, String s3) {
        if(s1==null||s2==null||s3==null||s1.length()==0||s2.length()==0||s3.length()==0){
            if((s1==null||s1.length()==0)&&(s2!=null&&s3!=null))return s2.equals(s3);//s1空,s2=s3
            if((s2==null||s2.length()==0)&&(s1!=null&&s3!=null))return s1.equals(s3);//s2空,s1=s3
            if((s3==null||s3.length()==0)&&((s2==null||s2.length()==0)&&(s1==null||s1.length()==0))) return true;//3个空
            return false;//3个中有空，其他的情形全部不符合
        }
        //出来要保证s1,s2,s3非null
        if(s1.length()+s2.length()!=s3.length())return false;
        boolean[][]dp=new boolean[s1.length()+1][s2.length()+1];
        for (int i = 0; i <= s1.length(); i++) {
            for (int j = 0; j <= s2.length(); j++) {
                if(i==0){
                    if(j==0)
                        dp[i][j]=true;
                    else
                        dp[i][j]=dp[i][j-1]&&s2.charAt(j-1)==s3.charAt(j-1);
                }else if(j==0){
                    if(i!=0)
                        dp[i][j]=dp[i-1][j]&&s1.charAt(i-1)==s3.charAt(i-1);
                }else
                    dp[i][j]=(dp[i-1][j]&&s1.charAt(i-1)==s3.charAt(i+j-1)) ||
                             (dp[i][j-1]&&s2.charAt(j-1)==s3.charAt(i+j-1));
            }
        }
        return dp[s1.length()][s2.length()];
    }

    public static void main(String[] args) {
        System.out.println(isInterleave("aa","ab","abaa"));
    }
}

数组降维：**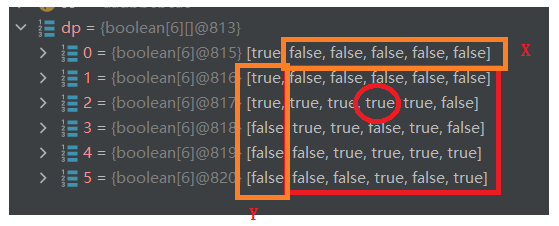

dp(i,j) 依赖于 dp(i,j-1) 和 dp(i-1,j) ，故可将 dp(i,j) 投影至 X，Y 轴 X(i)=Y(j)=dp(i,j)
下一个元素dp(i,j+1) 仅仅只需要从 X(j) 和 Y(i) 中获取状态即可，因此整个 dp 可以被降维
从而达到降维节省空间的目的。 将空间从 降至 。

要理解 dp(i,j) 的含义，X Y 仅仅是 dp 的投影 。

public static boolean isInterleave(String s1, String s2, String s3) {
    if(checkNull(s1,s2,s3)==false)return false;
    if(s1.length()+s2.length()!=s3.length())return false;    //3个串数目不一,定不可交错
    //出来要保证s1,s2,s3非null
    boolean []X=new boolean[s2.length()];//X轴存放s2 j 的信息
    boolean []Y=new boolean[s1.length()];//Y轴存放s1 i 的信息
    X[0]=(s2.charAt(0)==s3.charAt(0));
    Y[0]=(s1.charAt(0)==s3.charAt(0));
    //1.初始化X轴
    for (int i = 1; i < s2.length(); i++)  X[i]=(X[i-1]&&s2.charAt(i)==s3.charAt(i));
    //2.初始化Y轴
    for (int i = 1; i < s1.length(); i++)  Y[i]=(Y[i-1]&&s1.charAt(i)==s3.charAt(i));
    //3.状态转移
    for (int i = 1; i <= s1.length(); i++) {
        for (int j = 1; j <=s2.length() ; j++) {
            X[j-1]=(X[j-1]&&s1.charAt(i-1)==s3.charAt(i+j-1)) ||
                (Y[i-1]&&s2.charAt(j-1)==s3.charAt(i+j-1));
            Y[i-1]=X[j-1];
        }
    }
    return Y[s1.length()-1];// Y[s1.length()-1]应该和X[s2.length()-1]值一样
}

解题思路：DFS 深搜

大佬代码 🦄清晰简洁

class Solution {
    char[] cs1, cs2, cs3;
    boolean[][] mem;
    /**
     * 给定三个字符串 s1, s2, s3, 验证 s3 是否是由 s1 和 s2 交错组成的。
     * @return 若为交错而成，返回true，反之，返回false
     */
    public boolean isInterleave(String s1, String s2, String s3) {
        // 输入校验
        if (s1 == null || s2 == null || s3 == null)
            return false;
        int m = s1.length();
        int n = s2.length();
        // 边界判定，巴拉巴拉
        if (m == 0)
            return s2.equals(s3);
        if (n == 0)
            return s1.equals(s3);
        // 若长度不等，直接返回false
        if (m + n != s3.length())
            return false;
        // 初始化
        cs1 = s1.toCharArray();
        cs2 = s2.toCharArray();
        cs3 = s3.toCharArray();
        mem = new boolean[m + 1][n + 1];
        return dfs(0, 0, 0);
    }

    /**
     * dfs子方法
     * @param i 对应s1中的索引
     * @param j 对应s2中的索引
     * @param k 对应s3中的索引
     * @return s1,s2能否交错成s3
     */
    private boolean dfs(int i, int j, int k) {
        // 搜索到末尾时，成立
        if (i == cs1.length && j == cs2.length)
            return true;
        // 如果从ij出发的结果搜索过，那就不搜了
        if (mem[i][j])
            return false;
        // 判定条件与dp类似
        // 若当前s1的字符与s3的字符相同，看看下一个索引会怎样
        if (i < cs1.length && cs1[i] == cs3[k] && dfs(i + 1, j, k + 1))
            return true;
        // 若当前s2的字符与s3的字符相同，看看下一个索引会怎样
        if (j < cs2.length && cs2[j] == cs3[k] && dfs(i, j + 1, k + 1))
            return true;
        // 如果搜过都不成立的话，那么标记为访问过，并返回false
        mem[i][j] = true;
        return false;
    }
}