自然表达式转换为前/中/后缀表达式,其实是很简单的。
首先将自然表达式按照优先级顺序,构造出与表达式相对应的二叉树,然后对二叉树进行前/中/后序遍历,即得到前/中/后缀表达式。
1. 表达式的转换
举例说明将自然表达式转换成二叉树:
① 根据表达式的优先级顺序,首先计算 (b+c),形成二叉树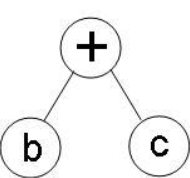
② 然后是 a×(b+c),在写时注意左右的位置关系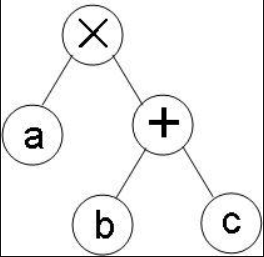
③ 最后在右边加上 -d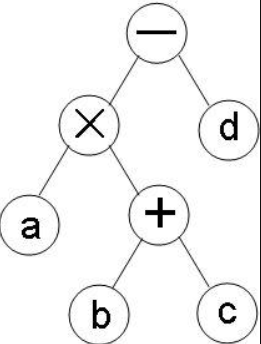
然后最这个构造好的二叉树进行遍历,三种遍历的顺序分别是这样的:
① 前序遍历:根-左-右
② 中序遍历:左-根-右
③ 后序遍历:左-右-根
所以还是以刚才的这个例子,在最终二叉树的基础上可以得出:
前缀表达式:-*a+bcd
中缀表达式:a*b+c-d
后缀表达式:abc+*d-
2. 前缀表达式求值
我们假设,输入的前缀表达式总是有效的,所以无需考虑特殊的场景,此题明显是一道用 栈 的题目。
方向很关键,和后缀表达式求值从左向右读取不同,前缀求值从右向左读取
- 遇到数字入栈
- 遇到操作符,根据操作符将栈中前两项拿出来进行计算,计算结果入栈
最终将表达式计算完毕,栈中剩余唯一数字就是结果,将其返回即可
3. 中缀表达式求值
我们假设,输入的中缀表达式总是有效的,所以无需考虑特殊的场景,此题正常计算。
4. 中缀表达式求值
我们假设,输入的后缀表达式总是有效的,所以无需考虑特殊的场景,此题明显是一道用 栈 的题目。
后缀表达式求值从左向右读取
- 遇到数字入栈
- 遇到操作符,根据操作符将栈中前两项拿出来进行计算,计算结果入栈
最终将表达式计算完毕,栈中剩余唯一数字就是结果,将其返回即可
4. 中缀表达式转前、后缀表达式
| 转换 | 中缀转前缀 | 中缀转后缀 |
|---|---|---|
| 栈 | 操作符栈 | 操作符栈 |
| 扫描顺序 | 从右到左 | 从左到右 |
| 遇到操作数 | 直接入栈 | 直接入栈 |
| 遇到右括号 | 直接入栈 | 将栈中操作符依次弹栈,直至遇到左括号,将左括号弹栈,处理完毕 |
| 遇到左括号 | 将栈中操作符依次弹栈,直至遇到右括号,将右括号弹栈,处理完毕 | 直接入栈 |
| 遇到其他操作符 | 检测当前与栈顶的优先级关系,如果当前大于等于栈顶优先级则将当前操作符入栈,否则将栈内元素全出栈,直至栈空或栈顶为 ( 或当前大于栈顶优先级时,才将当前操作符压入栈中 | 检测当前与栈顶的优先级关系,如果当前大于栈顶优先级则将当前操作符入栈,否则将栈内元素全出栈,直至栈空或栈顶为 ( 或当前大于栈顶优先级时,才将当前操作符压入栈中 |
| 操作符栈中的优先级 | 栈底到栈顶优先级:非递减。 即:栈顶可以大于或等于下面的 |
栈底到栈顶优先级:递增。 即:栈顶必须大于下面的 |
| 是否翻转 | 翻转 | 无需翻转 |

