[NC]132. 约瑟夫问题

🚩传送门：牛客题目
力扣题目

题目

这 个数字排成一个圆圈，从数字 开始，每次从这个圆圈里删除第 个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如：0、1、2、3、4这 5 个数字组成一个圆圈，从数字0开始每次删除第 3 个数字，则删除的前 4 个数字依次是2、0、4、1，因此最后剩下的数字是 **3** 。

进阶：空间复杂度 ，时间复杂度

示例 1：

输入: n = 5, m = 3 输出: 3

示例 2：

输入: n = 10, m = 17 输出: 2

解题思路：动态规划

本题是著名的 “约瑟夫环” 问题，可使用 动态规划 解决。

模拟法需要循环删除 轮，每轮在链表中寻找删除节点需要 次访问操作（链表线性遍历），因此总体时间复杂度为 。题目给定的 取值范围如下所示，观察可知此时间复杂度是不可接受的。

输入 ，记此约瑟夫环问题为 「 问题」 ，设解（即最后留下的数字）为 ，则有：

• 「 问题」：数字环为 ，解为 ；
• 「 问题」：数字环为 ，解为 ；
• 以此类推……

  请注意，数字环是 首尾相接 的，为方便行文，本文使用列表形式表示。

👉 定义： 表示约瑟夫环问题为 「 问题」 的最终剩余答案

对于 「 问题」 ，首轮删除环中第 个数字后，能够得到一个长度为 的新的数字环。🐛由于有可能 ，因此删除的数字为 ，删除后的数字环从下个数字（即 ）开始，设 ，可以得到下列新的数字环：

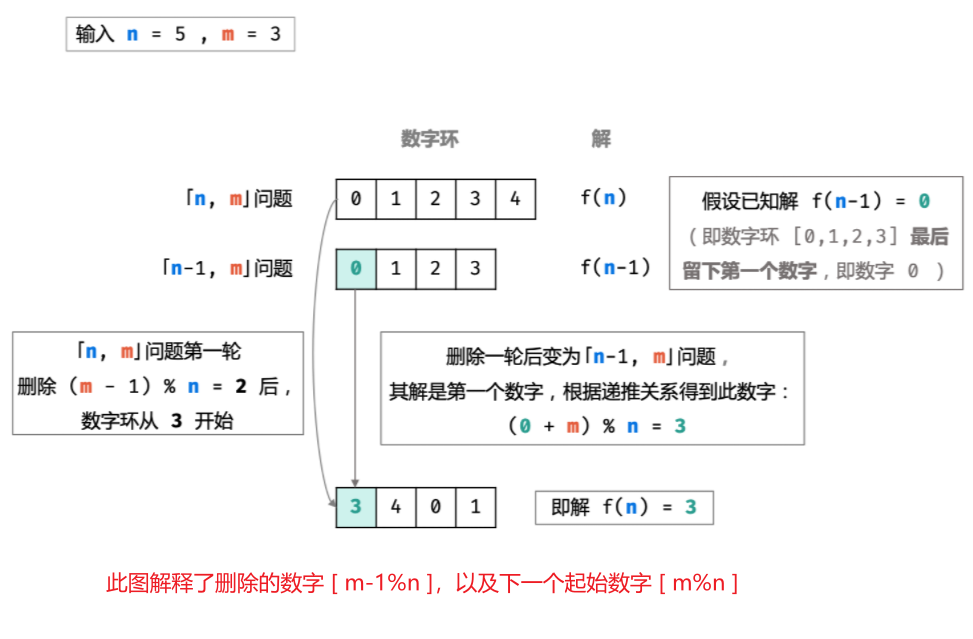
删除一轮后的数字环也变为一个「 问题」，观察以下数字编号对应关系：

👉 定义： 表示约瑟夫环问题为 「 问题」 的所有序列值

对于「 问题」中的 来说，其值范围 ，对于「 问题」删除后中的 来说，其值范围 ，因此需要找到 与 的关系 。设 与 我们需要找出 的映射关系 ：

🚩首先我们知道 是一定相等的

1. 首先在n个数序列中，删除第m个数字，会形成n-1个数序列
2. 接着在n-1个数序列中，删除第m个数字，会形成n-2个数序列
3. 接着在n-2个数序列中，删除第m个数字，会形成n-3个数序列
4. …
5. 接着在2个数序列中，删除第m个数字，会形成1个数序列，这就是结果

因此，在 个数字序列中不断删除第 个数字，按序列　　最终保留的结果是 ，则映射到序列 中最终保留的结果是 ：

备注：t=m%n由其定义得到的，可以看上面的🐛定义

最终发现了推导公式：

🚩

👉 定义： 表示约瑟夫环问题为「 问题」的最终剩余答案

一共i个数，从下标0开始，每次删除第m个数字，最终剩余的唯一一个数就是dp[i]。

边界条件： ,
🤣综上所述，我们不难发现，状态转移方程：

官方代码

class Solution {
    public int lastRemaining(int n, int m) {
        int []dp = new int[n+1];    // 默认初始化为 0
        for (int i = 2; i <= n; i++) {
            dp[i] = (dp[i-1] + m) % i;
        }
        return dp[n];
    }
}

最后我们发现，每次状态只与前一位的状态有关，因此我们可以进行空间优化，只保存前面的状态即可。

时间复杂度

时间复杂度：，其中 为序列的长度，需要循环 次。

空间复杂度：，需要额外使用长度为 的 数组，但是可以使用空间优化。

🚩官方代码

class Solution {
    public int lastRemaining(int n, int m) {
        int x = 0;
        for (int i = 2; i <= n; i++) {
            x = (x + m) % i;
        }
        return x;
    }
}