📈算法思想总结 - 🔖背包类问题总结 - 《LeetCode》

三类背包问题的区分
1.背包问题
- 常规题目
- 直白的列子（递归易于理解）
2.完全背包问题
3.多重背包问题

转自：https://www.cnblogs.com/fengziwei/p/7750849.html

由于自己 01 背包很弱，所以写下自己 01 背包问题的感悟，以供学习！

三类背包问题的区分

备注：重量和价值一定是固定的，只有数量可以波动

01背包

物品有重量、价值和数量，其中数量固定只有1个，只考虑重量和价值，在放和不放间思考，故而称作01背包

完全背包

物品有重量、价值和数量，其中数量不固定，可以有无数个，因此需要在数量、重量和价值中权衡。

多重背包

物品有重量、价值和数量，其中数量固定，有具体的N个，因此需要在数量、重量和价值中权衡。
2 2 6 5 4
6 3 5 4 6

1.背包问题

常规题目

Input 2 2 6 5 4 6 3 5 4 6 //背包承重： 10 第一行为wight 第二行为 value 一共5个物品 Output 01背包： 15 完全背包：30 //答案为在有限的空间内装最大价值的物品

//首先暴搜肯定能做，不谈

0-1背包问题是指每一种物品都只有一件，可以选择放或者不放。现在假设有n件物品，背包承重为m。对于这种问题，我们可以采用一个二维数组去解决：f[n][m]，其中n代表加入背包的是前n件物品，m表示背包的承重。故而f[n][m]表示当前容量能放进背包里面的物品的最大总价值（在n个物品中，m背包承重能装的最大总价值）。f[n][m]就是最终结果
动态规划：我们必须要知道初始状态和状态转移方程。
初始状态很容易就能知道，那么状态转移方程如何求呢？对于一件物品，我们有放进或者不放进背包两种选择：
我们的状态转移方程就是：f[n][m] = max( f[n - 1][m] , f[n - 1][m - weight[n]] + value[n])
（状态转移方程思想：比较第n个物品是放进去还是不放进去，最后的总价值大）

备注：

f[ n - 1 ][ m ] 代表第n个物品不放的最优解
- 第n个物品不放进去，故容量还是m，而f[n][m]变成了用 m 容量的背包从1到n-1个物品中找出最优解
f[ n - 1 ][ m - weight[ n ] ] + value[ n ] 代表第n个物品放进去最优解
- 第n个物品要放进去，故容量变成了m-weight[n] ，而f[n][m]变成了用m-weight[n]容量的背包，从1到n-1个物品中找出最优解。

解释：
（1）假如（第n个物品）我们放进背包，那么 f[ n ][ m ]=f[ n - 1 ][ m - weight[ i ] ] + value[ i ]
代码理解：

     - 本来原题是 m 承重的背包在 n 个物品中选择最大价值。
     - 由于第n个物品明确放入，所以现在的背包容量变成了m-weight[n]，**问题规模变小**
     - 问题变成了用 m-weight[n] 的容量从剩下的n-1个物品中选出最大价值

m - weight[n]这里，我们要明白：要把这件物品放进背包，就得在背包里面预留这一部分空间

（2）假如（第n个物品）我们不放进背包，那么 f[n][m] = f[n - 1][m]
代码理解：

     - 本来从n个中选择，但是明确第n个物品不放进去，结果就变成从n-1个物品中选择

（3）特殊的情况 f[n][m] = f[n - 1][m]
代码理解：

     - 就是背包容量放不下第n个物品。
     - 需要注意当n=1时候，若m<wight[1]，则 f[1][m]需置为零

下面是我写的代码注意点：

F[n][m]的含义是容量m的背包从n个物品中选择出总价值最大的可能
非常重要的一点我们在考虑从n个物品选择m重量的最大价值，为了便于理解**递归的方式的思考是
先考虑第n个能不能放，如果能放，就考虑第n个物品放不放，放不放取决于n-1个物品中的最大值，n-1个物品的最大值又由n-2个物品的最大值决定，……… 【规模变小的过程】
规模不断的缩小，最终达到第1个物品， mi 容量放不放，mi<第1个物品体积就是0，啥也装不下
因此 F[1][0]—-到——F[1][W[1]-1] 结果都是0 【容量太小，什么都放不进去】
F[1][W[1]]—-到—-F[1][m] 结果都是 V[1] 【只能装第一个物品】

直白的列子（递归易于理解）

假设有5个物品，重量为12345，价值也是12345，我有12的背包，我想求的答案是F[5][12]
第5个物品重量为5，价值也为5，我有12的背包显然能放下，所以我现在考虑的是为了价值最大
我究竟放不放第5个物品，这个取决于F[4][7] ( 第5个放 ) 和F[4][12] ( 第5个不放 ) 的值谁大，
这两个值我也不知道多少，好吧继续递归，F[4][7]的最大值又取决于第4个物品放不放，好吧和第5个物品一样了，变成了取决于F[3][3]和F[3][7]的值…..规模是不是在减少….最终会到底。
其中已知信息：

  -   F[1][0]---到----F[1][wight[1]-1] 结果都是0    【容量太小，什么都放不进去】
  -   F[1][wight[1]]---到---F[1][m] 结果都是 V[1]  【只能装第一个物品】

想法就和求斐波那契一样 F（n）=F（n-1）+F（n-2）

Fn不知道Fn-1 ，也不知道 Fn-2，但是F1知道F2也知道。
for循环呢就是先求F1，F2…..直到Fn，对应背包，就是F[1][0]——-F[1][m]，然后求F[2][0]—-F[2][m]
为了速度快，求出的 Fk 用表保存下来，以供后面使用

递归的解题思路：（为了加快速度用数组来保存中间计算结果）

# include<iostream>
# include<algorithm>
# define num 5
# define wight 10
using namespace std;
int F_[6][20];
int V[5], W[5];
//递归的写法
int f01(int n, int m) {
    //如果之前递归已经求出该值就返回
    if (F_[n][m] != -1)return F_[n][m];
    //此处考虑，n还能不能放进去
    if (m < W[n - 1])return  F_[n][m] = ((n == 1) ? 0 : f01(n - 1, m));
    else//能放进去，考虑n放不放的问题
        return F_[n][m] = max(f01(n - 1, m), f01(n - 1, m - W[n - 1]) + V[n - 1]);
}
int main(void) {
    memset(F_, -1, sizeof(F_));
    for (int i = 0; i < 5; i++)cin >> W[i];//录入重量
    for (int i = 0; i < 5; i++)cin >> V[i];//录入价值
    cout << "递归max：" << f01(num, wight) << endl;//递归求解
    system("pause");
    return 0;
}

动态规划状态转移方程是：f[n][m] = max( f[n - 1][m] , f[n - 1][m - weight[n]] + value[n])

正常动态规划的思路：

要明确F [i][j] 的意思，用 j 容量的背包，从 i 个物品中选择，其价值最大的值
要明确与递归中的区别，其中递归是人的思路，而动态规划则是计算机的思维方式。
要明确 F [ n ][ weight ]整个数组一开始是被默认初始化，全部置 0 的。
要明确思考的过程是从 第一个物品 开始的，而非上述递归中所讲的从 第n个物品 开始的。
要明确两部分值是已知的，即动态规划的初始态
- F[ 0 ][ 0 ] ——-到——-F[ 0 ][ wight ] 其值全部为 0
- F[ 1 ][ 0 ] ——-到——-F[ 1 ][ weight [ 0 ]-1] 其值全部为 0
```
- 备注：第一个物品重量为 weight[ 0 ]是因为 i 从1开始计数，但是weight数组是从 0 开始的
```
开始从第一个物品开始考虑，一直考虑到最后一个物品。 [ 第一层循环的 i —-物品]

假设当前考虑的是第 i 个物品，此时重量会从 0 一直循环到总背包重量m 。[ 第二层循环的 j —-重量]

首先考虑第 i 个物品能不能放进去，即当前背包容量是否容纳下第 i 个物品

- 不能放进去
      - 如果 **i** 是第一个物品，则 F [i][j]=0             [   什么东西都放不进去    ]
      - 如果 **i** 是其他物品，则** F[i][j] =F[i-1][j]  ** [ 其**F[ i-1 ][ j ]是已计算的 **]
         1. 为什么 F[i][j] =F[i-1][j] ？ 
            - 解释：**F[i][j]**代表的意思是用 **j **容量从**1到 i 个**物品中选择出最大价值，现在第 **i **个物品是装不下的。因此它的最大价值就等于用 **j **容量从**1到 i - 1 个**物品中选择出的最大价值，其值是已经计算过的 。
- 若能放进去
      - **F[i][j] = max(F[i - 1][j], F[i - 1][j - W[i - 1]] + V[i - 1]);      **
      - 因为能放进去，所以现在就是考虑放不放的问题了

# include<iostream>
# include<algorithm>
# define num 5
# define wight 10
using namespace std;
int V[5],W[5];
int F[6][20];
int main(void) {
    for (int i = 0; i < 5; i++)cin >> W[i];//录入重量
    for (int i = 0; i < 5; i++)cin >> V[i];//录入价值
    //状态转移方程：f[n][m] = max( f[n - 1][m] , f[n - 1][m - weight[n]] + value[n])
    for (int i = 1,j; i <=num; i++) {
        for (j = 0; j <= wight; j++) {
            if (j < W[i - 1]) {//第i个东西放不下
                F[i][j] = (i == 1 ? 0 : F[i - 1][j]);//分两种情形考虑是否是第一个物品
            }
            else {//放的下 考虑的是放不放
                F[i][j] = max(F[i - 1][j], F[i - 1][j - W[i - 1]] + V[i - 1]);
            }
        }
    }
    cout << "循环max：" << F[num][wight] << endl;
    system("pause");
    return 0;
}

0-1背包问题还有一种更加节省空间的方法，那就是采用一维数组去解决，下面是代码：

# include<iostream>
# include<algorithm>
# define num 5
# define wight 10
using namespace std;
int V[num+1], W[num+1];//为了逻辑上对应，让数据从下标1开始
int F[wight+1];
int main(void) {
    memset(F, 0, sizeof(F));
    for (int i = 1; i <= num; i++)cin >> W[i];//从1开始录入重量
    for (int i = 1; i <= num; i++)cin >> V[i];//从1开始录入价值
    //01背包
    for (int i = 1, j; i <= num; i++) {
    //    for (j = 0; j <= wight; j++) 正序的话其实是完全背包的解法，不需要考虑物品个数
        for (j = wight; j >= 0; j--) {//此处一定要倒序
            if (j >= W[i]) {//能够放下的时候考虑第i个物品放不放
                F[j] = max(V[i] + F[j - W[i]], F[j]);
            }
            else
                F[j] = F[j] ? F[j] : 0;//放不下就是原来的值
        }
    }
    cout << "循环max：" << F[wight] << endl;
    system("pause");
    return 0;
}

首先肯定很多人疑惑，为啥第二个循环是倒序……
其实我一开始也疑惑，我认为正序完全可以做，后来尝试发现不可以，必须要倒序

这里说下我个人对于倒序的理解：【这段思考是错误的！！！！！！！！】

重要的一点说明下：对于代码中的F[m]的含义为：m容量的包所能装下的最大价值。
开始我想，从0—m承重开始循环，如果当前的物品能放进去，那么当前的质量就会变成 m-wight[ i ]
- 由于 m-wight[i] < m，在之前的操作中，F[m-wight[i]]的最大值一定是已知的。

显然这个F[m]的选择取决于F[m]=max(F[m-wight]+V[i],F[m])

1. 至于为啥和F[m]比较 ？
   - 答案：很简单，之前的**F[m]**在**i-1**个物品中已经求解出不放入第** i **件物品的最大值，那么现在只要考虑放进去后的值是否大于不放进去的值即可，这么一看确实逻辑上没有一点问题。

但是，但是，但是，最要的东西说三遍！如果正序承重从0-m，会重复多放物品，导致数据错误。

举个例子吧：下图为例，i=1 为 a 物品，i=5 为 e 物品

当 i=1，考虑第一个物品 a 的时候，总容量 m ,其中容量为 0，1 都放不进去，F[0，1] 总价值均为0
到了容量 2 的时候刚好能放进去，总价值为6，没问题，一直到容量3也没有问题。
但是到了容量为4会出现一个问题，这时候发现第 i 个物品（就是例子的物品 a ）又可以放进去。

若物品 a 放进去还会剩下2个容量，F[2]=6之前算过

  - 就会出现这种情况 **F[4]=max(F[4-2]+V[1],F[4]) **, 导致F[4]=12,第1个物品被放进了2次。        
     - 备注：其中 F [4] 开始为 0

当容量到 6 时，发现，物品 a 被放入3次，容量 8 被放入4次，容量10被放入5次

结论：如果正序承重从0-m，会重复多放物品，导致数据错误。

【后来我才发现其实这个是完全背包的一维数组解法】(纯属意外惊喜)

现在解释为啥倒过来就不会出现这种情况？

很简单，首先明确 F 数组是初始化为0的
要明白 F[m]的含义为：m容量的包所能装下的最大价值。
当容量从weight开始递减的时候，我们在考虑第1个物品能不能放进去，由于容量10,9,8,7,6,5,4,3,2，物品a都能被放进去。故而F[10,9,8,7,6,5,4,3,2]=6,其中容量1，0的时候物品a不能放进去，故而F[1,0]=0 。
不会重复放入。

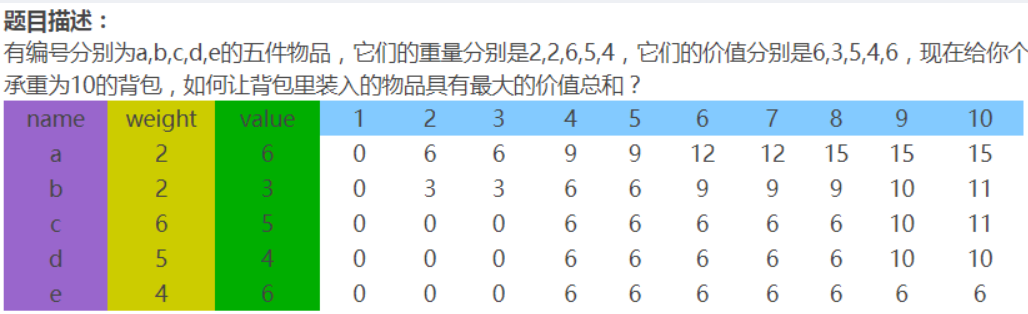图从下向上看

2.完全背包问题

完全背包问题是指每种物品都有无限件

解法就是刚才的一维数组的解法，只不过内循环用正序。

    for (int i = 1, j; i <= num; i++) {
        for (j = 0; j <= wight; j++) {
            if (j >= W[i]) {//能够放下的时候考虑第i个物品放不放
                F[j] = max(V[i] + F[j - W[i]], F[j]);
            }
            else
                F[j] = F[j] ? F[j] : 0;//放不下就是原来的值
        }
    }

为啥正序就变成了完全背包的解法？
解释：这个其实还是很好理解的，因为在正序的基础上，我们其实不用考虑第 i 个物品的个数，我们只需要不停的考虑它能不能放进去，如果能放进，剩余的空间还能够放下的最大值和第i个物品的价格能否大于当前F[m]的价值。

客官还是好好想想….

代码也可以优化成：

不在从0—-到—-m
而是从wight[i]—-到—-m
```
 for (int i = 1; i <= n; i++) {
     for (int j = weight[i]; j <= m; j++) {
         f[j] = max(f[j], f[j - weight[i]] + value[i]);
     }
 }
```
这个也很好理解承重 j 如果小于weight[i]，那么说明第 i 个物品放不下，F[ j ]的值不会变化还是 i-1时候求解的F[j]

3.多重背包问题

多重背包意思就是：物品有个数，重量，价值。

说实话，其实没必要说那么多，为啥，因为很简单，当你看懂01背包的那一刻你已经就能求解多重背包和完全背包了，为啥？
因为完全背包可以转化为多重背包，多重背包可以转化为01背包

至于为啥要说那是为了专精一种问题的求解。

1.完全背包可以转化为多重背包

至于为啥可以转化，也很简单，完全背包虽然说物品的个数有无数个，但是由于承重m已经确定，每个物品又有重量，导致其实单一装1种物品的时候，每个物品能装的最大值已经出来了，至于更多的数量也没有意义，因为装不下。这时候由于每种物品都有了数量，导致完全背包变成了多重背包。

2.多重背包可以转化为01背包

多重背包转化01也很简单，物品1有2个，价值为4，我们可以转化为 a ，b物品，价值都是4。然后就变成了01背包问题了。
但是我们知道多重背包如果一个一个转化为01背包还是非常慢的，这里我最近又学习了一种方法，所以特地加进了文章，那就是多重背包转化01背包利用二进制优化。

二进制优化：（有点惊为天人，牛逼！🚩 ）
大家知道任意一个十进制数都可以转换成二进制，那么假设某种物品有1023种，即210-1，二进制为111111111，则可以视为每一位分别是一个由｛1，2，4，8，16，32，64，128，256，512｝个物品糅合成的大物品，二进制数每一位0表示不取，1表示取，这样我们就可以取遍所有的数，而若不是2的整数幂-1个物品，再补上缺的物品个数就好了，比如1025，就再补上个由2个物品组成的新物品。

例如把22进行二进制拆分：
成为1,2,4,8,7；由1,2,4,8可以组成1—15之间所有的数，而对于16—22之间的数，可以先减去剩余的7，那就是1—15之间的数可以用1,2,4,8表示了。

理解：
其实相当于我们将二进制中的每一位当做一个物品，如1111，就是我们将 10 当做一个物品
代码中相当于将 1，10，100，1000 当成4个物品
利用这4个物品可以表示出十进制 0-15 中的所有组合可能性
因为0代表取，1代表不取，在考虑的过程中间接的列出了所有可能。

多重背包转化01背包的代码：

    for (int i = 1, j; i <= num; i++) {
        for (int k = 0; k < num[i]; k++) {//加上个数当做别的物品只不过价值和重量和i物品一样
            for (j = wight; j >= 0; j--) {//倒序求解01背包
                if (j >= W[i]) {//能够放下的时候考虑第i个物品放不放
                    F[j] = max(V[i] + F[j - W[i]], F[j]);
                }
                else
                    F[j] = F[j] ? F[j] : 0;//放不下就是原来的值
                }
        }
    }

多重背包转二进制问题代码：

    memset(F, 0, sizeof(F));//F初始化0
    for (int i = 0; i < 5; i++)cin >> W[i];//录入单个重量
    for (int i = 0; i < 5; i++)cin >> V[i];//录入单个价值
    for (int i = 0; i < 5; i++) {//依次录入数量
        cin >> nu[i];
        for (int j = 1; j <= nu[i]; j <<= 1) {//数量开始二进制拆分
            value_[k] = j*V[i];//总价值=个数*单价
            wight_[k++] = j*W[i];//总重量=个数*单重
            nu[i] -= j;//剩余个数更新
        }
        if (nu[i]) {//剩余部分存储
            value_[k] = nu[i] * V[i];
            wight_[k++] = nu[i]*W[i];
        }
    }//以上步骤将多重背包二进制转化为01背包
    //下述为01背包做法
    for (int i = 0, j; i < k; i++) {//个数
        for (j = wight; j >= 0; j--) {//倒序质量
                if (j >= wight_[i]) {//能够放下的时候考虑第i个物品放不放
                    F[j] = max(value_[i] + F[j - wight_[i]], F[j]);
                }
                else
                    F[j] = F[j] ? F[j] : 0;//放不下就是原来的值
            }
        }

最后补充的一点：以上所有做法的参考量都是重量，我们都是从背包承重开始考虑的，但是其实背包问题也可以从其他方面开始考虑，比如说价格，它的本质状态转移方程思想并没有变化，例如价格依旧：

F[value]=max(F[value]，F[value-value[i]]+value[i])

不管怎么考虑，顺序还是从第i个物品开始考虑，这东西我能不能拿，能拿了的话，我到底拿不拿？