Catalan 组合数（卡塔兰数）

卡塔兰数**是组合数学中一个常在各种计数问题中出现的数列。

卡塔兰数的一般公式为 。

令 h(0)=1,h(1)=1，Catalan满足递归式：h(n)= h(0)*h(n-1) + h(1)*h(n-2) + ... + h(n-1)h(0),n>2

还可以化简为1阶递推关系: 如 `h(n)=(4n-2)/(n+1)h(n-1)(n>1) h(0)=1*`

理解应用和公式推导

(1).出栈次序问题**
一个栈(无穷大)的进栈序列为1,2,3,..n，有多少个不同的出栈序列?

关于这个问题的5种变型

(2).找零钱（找一半）**

有 2n 个人排成一行进入剧场。入场费5元。其中只有 n 个人有一张 5 元钞票，另外 n 人只有 10元钞票，剧院无其它钞票，问有多少种方法使只要有10元的人买票，售票处就有5元的钞票找零？

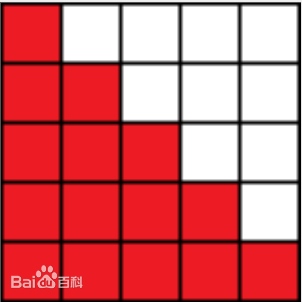
(3).三角网格
形如这样的直角三角形网格，从左上角开始，只能向右走和向下走，问总共有多少种走法 ？

                                          ![](https://cdn.nlark.com/yuque/0/2021/png/2955945/1618042490105-440cd2e8-be22-4ffd-9368-5466a43e5a86.png#align=left&display=inline&height=302&margin=%5Bobject%20Object%5D&originHeight=302&originWidth=302&size=0&status=done&style=none&width=302)<br />**<br />**<br />**(4).括号排列**<br />**<br />矩阵连乘：![](https://cdn.nlark.com/yuque/__latex/77ffffd08cbfd645484e6a62ae489341.svg#card=math&code=P%3Da_0%5C%20.%5C%20a_1%5C%20.a_3%5C%20....%5C%20a_n&height=18&width=140) ，共有`（n+1）`项，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？或者说：有`n`对括号，可以并列或嵌套排列，共有多少种情况？

(5).球盒问题

球分两种颜色，黑色和白色分别各有 n 只，盒子数量和球的个数相同，每个盒子里面只能放一只球，并且必须满足如下限制,即每一个白球必须和一只黑球配对（白球在黑球前，允许嵌套**）。

例：用0表示白球，1表示黑球

0011，010101，001011合法。 1100，101010，010110不合法。